 |
Методы расчета системы электроснабжения по графику движения поездов и результат тяговых расчетов.
|
|
|
|
Методы расчета системы электроснабжения по графику движения поездов и результат тяговых расчетов.
Методы электрического расчета, основанные на графике движения поездов, заключаются в том, что требуемые величины определяют последовательно для ряда моментов времени исходя из заданного графика движения поездов и кривых потребления активного и реактивного тока каждым из них. По данным расчетов строят график изменения величины (нагрузки питающей линии, потери мощности в контактной сети, потери напряжения на токоприемнике и т. д. ) в зависимости от времени. На основании этих графиков находят максимальные, средние и среднеквадратичные значения интересующих величин в течение рассматриваемого периода времени. Преимуществом такого метода является возможность для заданного графика движения поездов и кривых изменения тока, потребляемого поездами каждого типа при движении их по участку, наиболее точно определить все величины, установление которых необходимо при проектировании и эксплуатации устройств электроснабжения.
При применении метода расчета, основанного на графике движения поездов, в процессе проектирования требуется осуществить выбор расчетного графика, который был бы характерен для заданных размеров движения, скорости и веса поездов. Подобный расчетный график движения поездов при проектировании электрификации железнодорожных линий на перспективу можно установить лишь приближенно. Поэтому практически не может быть реализована та большая точность результатов расчета, которую принципиально позволяет получить данный метод при заданном графике движения поездов. Этот метод требует значительной затраты времени на производство электрических расчетов, особенно при определении средних значений расчетных величин в течение длительного периода времени. В связи с этим метод электрического расчета, основанный на графике движения поездов, практически используют не так часто, главным образом для определения максимальных значений расчетных величин.
|
|
|
Метод равномерного сечения графика движения поездов основан на наличии в качестве исходных данных тяговых расчетов для поездов всех типов, обращающихся на данном участке, или исполненных кривых потребления токов этими поездами и графика движения поездов за расчетный интервал времени Т (рис. а, б).
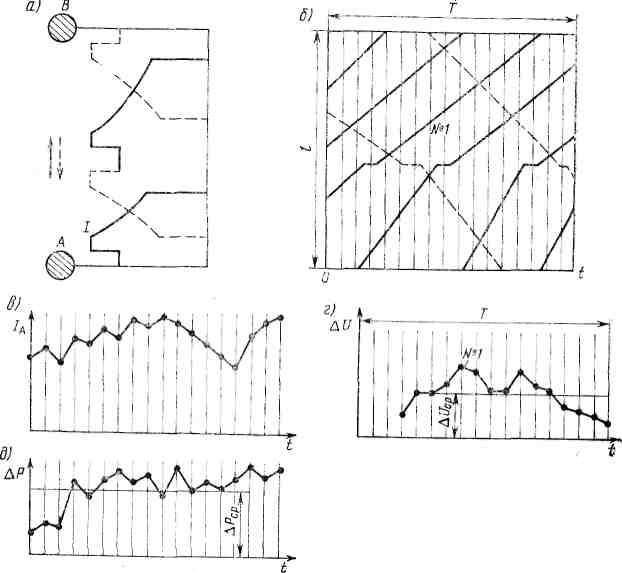
Масштабы пути при построении графика движения поездов и кривых потребляемого тока должны быть одинаковыми, а начальные точки пути - совпадать между собой. Кривые потребления тока и движения поездов на графике показаны сплошными линиями для поездов прямого и штриховыми - обратного направления.
Если на участке обращаются поезда различного типа (грузовые разного веса, пассажирские и т. д. ), то для каждого типа поезда строят свою кривую изменения потребляемого тока.





По этому методу мгновенные схемы расположения поездов берутся по графику движения через одинаковые (равномерные) интервалы времени.
Решая последовательные мгновенные схемы (в нашем примере на рис. б их восемнадцать), получаем токи подстанций, потерю напряжения до токоприемника выбранного поезда, потери мощности в тяговой сети для каждой мгновенной схемы. Полученные значения наносят на графики зависимости этих величин от времени (рис. в, г, д) в последовательном порядке расчета мгновенных схем. Смежные значения расчетных величин соединяются между собой прямыми отрезками. Степень точности получения расчетных величин зависит от интервала между смежными сечениями. Чем больше сечений берется за один и тот же интервал времени, тем больше точность расчета.
|
|
|

При проектировании принимают интервал 1—2 мин. Вместе с тем при любом интервале не исключена возможность непопадания в расчетные мгновенные схемы характерных моментов, в которые включаются или отключаются двигатели электровозов или появляются на фидерной зоне новые электровозы.
Таким образом, используя метод сечения графика, определение той или иной величины при изменяющихся месторасположении и величине нагрузок можно свести к решению ряда задач, в каждой из которых величина и месторасположение нагрузок неизменны. Точность расчета в значительной мере зависит от того, как выбраны моменты времени, в которые производится сечение графика. Точность получаемых результатов тем выше, чем меньше выбраны интервалы.
Полученные зависимости электрических величин от времени (рис. в, г, д) на расчетном интервале времени Т позволяют найти все их значения.
Среднее значение тока подстанции
IАср = 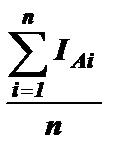
где IАi – значение тока подстанции в i -ймгновенной схеме;
n – полное количество мгновенных схем за период Т.
Действующее значение тока подстанции
IАэ = 
Среднее значение потери напряжения на токоприемнике расчетного электровоза за период Т (в примере за расчетный принят электровоз № 1) за время хода его по зоне
Δ Uср = 
где Δ Ui – потеря напряжения до токоприемника данного выбранного поезда в i -й мгновенной схеме.
Средние потери мощности в тяговой сети за период Т
Δ Рср = 
где Δ Рi – потери мощности в тяговой сети в i -й мгновенной схеме.
Средние потери энергии в тяговой сети за расчетный период вре-
мени Т
Δ А = Δ Рср · Т
где Т — расчетный период времени, ч.
Недостатком метода равномерного сечения графика является то, что точки, в которых происходит резкое изменение нагрузок, потребляемых отдельными поездами (включение или переключение тяговых двигателей), как правило, не совпадают с точками сечения графика. Это несколько снижает точность получаемых результатов, особенно при определении максимальных величин.
Более точные результаты могут быть получены, если сечение графика производить не через одинаковые промежутки времени, а по характерным точкам, т. е. точкам, в которых происходит резкое изменение нагрузки (рис. 43). Такой способ расчета называют методом характерных сечений графика движения.
|
|
|
Методы расчет3. Методы расчета системы электроснабжения по графику движения (Р. Р. Мамошин)
Р
Рис. 97. К расчету методом равномерного сечения графика движения
|
|
Определять ДЛГ и Лг по мгновенным схемам очень сложно. Проще определять эти величины по средним размерам движения.
Метод характерных сечений позволяет существенно повысить точность расчетов. Для этого действительную кривую потребления тока (рис. 98, а) заменяют спрямленной кривой (рис, 98, 6, в), на которой предварительно намечают характерные точки (помечены цифрами). Характерные точки намечают в узлах изменения тока [12].
Часто действительные кривые потребления тока изменяются (см. рис. 98, б) и дополнительно упрощаются (см. рис. 98, б)
|
|
| tj tz tj. tt, t5 tj t^t^t. |
Рис. 98. К расчету методом характерных сечений графика движения
за счет пренебрежения участками пуска электровоза (целесообразно производить такое упрощение при расчетах магистральных электрифицированных дорог, где пуски редкие).
 При таком подходе к кривым потребления тока поездами интервал между мгновенными схемами выбирают не произвольно-, а так, чтобы в них попадали нагрузки поездов во всех характерных точках. Для этого через все характерные точки кривых потребления токов на графике движения за расчетный интервал времени Т проводят горизонтальные штрих-пунктирные линии /—/, 2—2 и т, д. (рис, 98, г).
При таком подходе к кривым потребления тока поездами интервал между мгновенными схемами выбирают не произвольно-, а так, чтобы в них попадали нагрузки поездов во всех характерных точках. Для этого через все характерные точки кривых потребления токов на графике движения за расчетный интервал времени Т проводят горизонтальные штрих-пунктирные линии /—/, 2—2 и т, д. (рис, 98, г).
Помимо нанесенных штрих-пунктирных линий, имеются дополнительные сечения, совпадающие с осями подстанций Ли В и станцией N.
Таким образом, количество мгновенных схем, интервалы между ними являются функцией расположения характерных точек на тяговых расчетах.
Ось подстанции В совпадает с характерными точками а и б па тяговом расчете поезда нечетного направления. Следовательно, пе-
ресечение этой оси с графиками движения поездов № 5 и 7 определяет необходимость рассмотрения двух мгновенных схем (штриховые с двумя точками вертикальные сечения t& и t^). Пересечение линии /—1 с этими же поездами определяет потребность рассмотрения еще двух мгновенных схем (t8 и t2i). Линия 5—5 пересекает графики движения трех нечетных поездов —№ 3, 5, 7. Ось станции N соответствует характерным точкам пуска поездов четного и нечетного направлений № 3, 4, 5, 6, 8. Этим получают еще пять мгновенных схем (сечение t$, t%, t\$, t\s, t25).
|
|
|
|
|
Аналогичным образом определяют мгновенные схемы для нечет
ных поездов по линиям 6—6, 7—7, 8—8. Линия 7—7 является об
щей для характерных то
чек нагрузок поездов чет
ного и нечетного направ
лений (№ 3, 4, 5, 6, 8).
Также определяются
мгновенные схемы по характерным точкам тягового расчета поездов четного направления (линии 2—2, 4—4, 9—9, 10—10 и ось подстанции А). Сечения этих мгновенных схем см. на рис. 98, г.
|
S) |
| h ^ |
|
|
|
г) |
| Рис. 99. К расчету тока фидера методом непрерывного исследования графика в схеме одностороннего питания однопутного участка |
На графике движения поездов утолщенными точками показаны те поезда, характерные точки нагрузок которых послужили причиной необходимости рассмотрения мгновенной схемы в данный момент времени. В каждой мгновенной схеме есть хотя бы одна характерная точка одного поезда. Если характерные точки поездов разных направлений в данной мгновенной схеме совпадают (например, мгновенная схема в
сечении tis), то результирующая нагрузка в данной схеме является алгебраической суммой нагрузок.
В выбранные таким образом сечения графика движения поезда представляются теми нагрузками, которыми они попадают в данное сечение. Например, в мгновенную схему, соответствующую сечению t2, поезд № 1 не попадает, так как на этом участке пути в соответствии с тяговым расчетом нечетный поезд нагрузки не потребляет. Поезд № 4 четного направления в это сечение не попадает по той же причине. Поезд № 3 нечетного направления в это сечение попадает нагрузкой /3, а поезд № 2 — промежуточным значением тока 12. Таким образом, в этой мгновенной схеме (соответствующей сечению t2) оказываются задействованными поезда № 2 и 3.
Аналогично находят нагрузки поездов во всех остальных схемах. Последовательность решения мгновенных схем определяется только временем их появления в графике движения, а методы решения схем и расчетные формулы остаются теми же.
Метод непрерывного исследования графика движения отличается от описанных выше методов тем, что при построении нагрузок элементов тяговой сети используются полностью тяговые расчеты поездов без спрямления их характеристик. Для выполнения расчетов тяговые расчеты для всех типов поездов перестраиваются в зависимости от времени. Для каждого типа поезда заготавливается обычно столько зависимостей /Пг(0 для рассчитываемой фидерной зоны, сколько поездов этого типа может одновременно оказаться на зоне [12].
|
|
|
Построение графиков нагрузок фидеров зависит от схемы питания поездов. При односторонней схеме однопутного участка построение графика нагрузки сначала ведут автономно по поездам, а затем составляют полную картину нагрузки фидера.
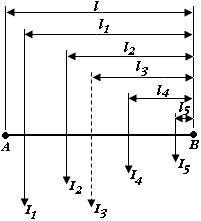
Пусть дан график движения поездов за период времени Т (рис. 99, а), в течение которого по фидерной зоне проходят два типа поезда № 1 и 3. Кривые тяговых расчетов /m (t) и 1д3 (t) за время хода поездов по зоне размещаются под графиком движения так, чтобы начала тяговых расчетов совпадали с моментами появления поездов на фидерной зоне (рис. 99, бив). На отрезке" времени t\ на зоне имеется только ток поезда № 1 и ток фидера равен току этого поезда. На отрезке времени t2 ток фидера равен сумме токов поездов № 1 и 2, а на отрезке t3 — току поезда № 3. Все эти построения выполнены на рис. 99, г. Результирующая кривая здесь представляет собой ток фидера.
|
|
|
|
|
|
При двусторонней схеме питания однопутного участка все построения остаются такими же, но при этом необходимо учитывать токораспределение между подстанциями.
Обычно токораспределение нагрузки каждого поезда между подстанциями зоны выполняют графически. Такое графическое токораспределение производят на основании известной из геометрии теоремы о пропорциональном делении отрезка. Пусть (рис. 100, а) отрезок DL означает в определенном масштабе нагрузку поезда на зоне между подстанциями А и В, а 1А и 1В — расстояние от этой нагрузки до. подстанций А я В. Если провести из точки D линию, параллельную отрезку АВ, до пересечения ее в точке С с перпендикуляром, восстановленным к точке А, а точку С соеди-нить с точкой В, то в результате построений получим ACDE~ ~ABEF (три угла одного треугольника равны трем углам другого треугольника). Учитывая, что CD = AF = lA, 0. ) с BF = lB, получаем
c/b=lA/h-
 Этим способом производят графическое деление нагрузок каждого поезда непосредственно по тяговому расчету /„(*) Щ™шщщ, на фидерной зоне. Для ^ примера на рис. 100, б графически распределена нагрузка поезда, потребляющего на зоне АВ ток на участке между точками С н F. Следовательно, при двустороннем питании однопутного участка сначала ток поезда каждого типа Im(t) указанным здесь способом графически распределяется между подстанциями, а затем осуществляют необходимые построения, подобные тем, которые выполнены на рис. 99. При этом на выходе получаем кривые /фд(^) и /фв(/). Для получения кривой /фд(/) необходимо суммировать заштрихованные площади, а для получения кривой/фВ(^) — н«заштрихованные (рис. 101).
Этим способом производят графическое деление нагрузок каждого поезда непосредственно по тяговому расчету /„(*) Щ™шщщ, на фидерной зоне. Для ^ примера на рис. 100, б графически распределена нагрузка поезда, потребляющего на зоне АВ ток на участке между точками С н F. Следовательно, при двустороннем питании однопутного участка сначала ток поезда каждого типа Im(t) указанным здесь способом графически распределяется между подстанциями, а затем осуществляют необходимые построения, подобные тем, которые выполнены на рис. 99. При этом на выходе получаем кривые /фд(^) и /фв(/). Для получения кривой /фд(/) необходимо суммировать заштрихованные площади, а для получения кривой/фВ(^) — н«заштрихованные (рис. 101).
Рис. 102. К распределению нагрузки поезда нечетного направления между фидерами подстанций при узловой схеме
При односторонней схеме питания двухпутного участка и отсутствии поперечных соединений контактных подвесок путей нагрузка фидера любого пути определяется так, как это делается при одностороннем питании однопутного участка. Если питание двухпутного участка осуществляется от одного фидера, а соединение " контактных подвесок выполнено в конце фидерной зоны, то расчет нагрузки фидера ведут как для однопутного участка.
Если соединение фидеров путей осуществляется в пункте Я (рис. 102, г) на расстоянии 1\ от подстанции А, а подстанция В отсутствует, то, перейдя от кольцевой схемы питания к двусторонней, получаем схему расположения поездов в соответствии с рис. 102, д. В узле Я появляется эквивалентная /экв суммарная нагрузка участков 12 обоих путей. Эта нагрузка делится поровну между фидерами Л] и А2, если сечения подвесок обоих путей одинаковы или в отношении z0i/z02, если сечения различны (здесь zol и z02 удельные сопротивления подвесок путей), при постоянном токе — Гм и г02. Остальные нагрузки разносятся между фидерами А\ и А2 обычным образом.
При схеме двустороннего питания двухпутного участка и отсутствии поперечных связей контактных подвесок путей расчет нагрузок фидеров ведут так же, как и для схемы, двустороннего питания однопутного участка.
В случае наличия поста секционирования (рис. 102, а) в питании каждого поезда участвуют все четыре фидера. Допустим, имеется тяговый расчет для поезда нечетного направления данного типа /ц(/) по фидерной зоне (рис. 102, б). Распределение нагрузок между подстанциями не зависит от количества и мест расположения пунктов поперечного соединения контактных подвесок путей и поэтому оно. определяется как для однопутного участка с двусторонним питанием. На рис. 102, 6 заштрихованная часть графика является зависимостью 1А (I), а незаштрихованная —/в (/).
Поезд данного типа, перемещаясь по зоне, может находиться либо на участке А\П, либо на ПВ{. Когда поезд находится на участке А\П, то ток h, посылаемый поезду подстанцией В, делится поровну между фидерами В\ и В2 и поэтому ординаты сложной фигуры 1—2—3—4—5—6—7—1 (см. рис. 102, 6) делятся поровну между собой и являются нагрузками фидеров В\ и В2 (рис. 102, в). Когда поезд идет по участку ПВи то ток 1А, посылаемый поезду подстанцией А (фигура 5—8—9 на рис. 102, б), делится поровну между фидерами Ал и А2 (см. рис. 102, в). Ток, посылаемый подстанцией В поезду, когда он находится на участке ПВи распределяется между фидерами В\ и В2 (трапеция 8—10—4—5 на рис. 102, б) так, как если бы подстанция В была разделена на два источника и участок контактной сети Вх—Я—В2 получал питание с двух сторон (через В{ и В2) только от разделенной на два источника подстанции В. Иными словами, ток 1В на этом участке распределяется между фидерами Вх и В2 обратно пропорционально расстояниям от поезда до узла В\ и от поезда до узла В2 (через узел Я поста). Аналогично распределяется нагрузка подстанции А между фидерами Ах и А2 (1—7—6—5—9—0 на рис. 102, 6), когда поезд находится на участке АХП (см. рис. 102, в). Для поездов четного направления нагрузки фидеров определяются аналогичным образом.
Подготовив таким образом кривые тяговых расчетов поездов всех типов четного и нечетного направлений и перестроив их в функции /фг(0. можно построить суммарные графики нагрузок фидеров подстанций в зависимости от времени, а по ним — графики -потерь напряжения и мощности в тяговой сети.
Кондратьев 
|
|
|







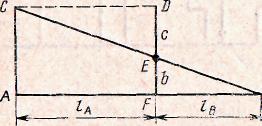
 Рис. 100. Деление тока поезда между двумя подстанциями графическим способом
Рис. 100. Деление тока поезда между двумя подстанциями графическим способом