 |
Показатели точности уравнения регрессии и оценок его параметров
|
|
|
|
При анализе уравнения регрессии сначала проверяется значимость уравнения регрессии в целом. Для решения этой задачи используется процедура дисперсионного анализа, основанная на разложении общей суммы квадратов отклонений зависимой переменной (SST – Sum. Squared total) на две составляющие: одна из которых – за счёт регрессионной зависимости (SSM – Sum. Squared model), другая – за счёт остаточного члена (SSR – Sum. Squared residual):
SST = SSM + SSR
или

Следует иметь в виду, что это соотношение верно, если в уравнении регрессии присутствует константа. Разделив суммы квадратов отклонений на соответствующие числа степеней свободы, получим суммы квадратов на одну степень свободы или средние квадраты, которые являются оценками дисперсии  зависимой переменной y или остатков
зависимой переменной y или остатков  в условиях разных предпосылок. Одна из этих оценок (MSM = SSM/m) рассчитывается в предположении, что все коэффициенты в модели регрессии равны нулю (Ho:
в условиях разных предпосылок. Одна из этих оценок (MSM = SSM/m) рассчитывается в предположении, что все коэффициенты в модели регрессии равны нулю (Ho:  =
=  =…=
=…=  =0), а другая (MSR = SSR/(n–m–1)) – в предположении, что не все коэффициенты регрессии равны нулю. Затем эти оценки сравниваются по F-статистике (F =
=0), а другая (MSR = SSR/(n–m–1)) – в предположении, что не все коэффициенты регрессии равны нулю. Затем эти оценки сравниваются по F-статистике (F =  ), которая в случае выполнимости предпосылок МНК и верности нулевой гипотезы имеет распределение Фишера с числом степеней свободы числителя, равным m и знаменателя – (n – m – 1). Расчётное значение F-статистики сравнивается с критическим и если F
), которая в случае выполнимости предпосылок МНК и верности нулевой гипотезы имеет распределение Фишера с числом степеней свободы числителя, равным m и знаменателя – (n – m – 1). Расчётное значение F-статистики сравнивается с критическим и если F  , то нулевая гипотеза отклоняется, и уравнение регрессии признаётся значимым.
, то нулевая гипотеза отклоняется, и уравнение регрессии признаётся значимым.
Вернёмся ещё раз к MSR. Этот показатель является одной из характеристик точности уравнения регрессии. Его называют остаточной дисперсией и обозначают S  . Можно показать, что MSR является несмещённой оценкой дисперсии
. Можно показать, что MSR является несмещённой оценкой дисперсии  .
.
MSR также используется при вычислении других показателей точности уравнения регрессии. Например, корень квадратный из MSR называется стандартной ошибкой оценки по регрессии(Sy,x) и показывает, какую ошибку в среднем мы будем допускать, если значение зависимой переменной будем оценивать по найденному уравнению регрессии при известных значениях независимых переменных. Имеем
|
|
|
Sy,x = 
Кроме того, этот показатель в неявном виде участвует в определении ещё одного показателя точности уравнения множественной регрессии, а именно – коэффициента множественной детерминации (R – squared или R2). Как известно,

или после преобразований (в случае, если в уравнении регрессии присутствует константа)

Отсюда следует, что коэффициент множественной детерминации показывает долю вариации зависимой переменной, обусловленную вариацией включённых в уравнение регрессии независимых переменных, или, иными словами, долю вариации зависимой переменной, обусловленную регрессионной зависимостью.
Коэффициент множественной детерминации изменяется от нуля до единицы и равен единице, если SSR = 0, (связь линейная, функциональная), и равен нулю, если SST = SSR, (линейная связь отсутствует).
Из определения коэффициента множественной детерминации следует, что он будет увеличиваться при добавлении в уравнение регрессии независимых переменных, как бы слабо не были они связаны с независимой переменной. Следуя этой логике, в уравнение регрессии для увеличения точности отражения изучаемой зависимости может быть включено неоправданно много независимых переменных. Точность уравнения при этом может увеличиться незначительно, а размерность модели возрасти так, что её анализ будет затруднён. Кроме того, при этом уменьшается число степеней свободы модели и ухудшается точность оценок. Для преодоления этого недостатка был разработан исправленный (на число степеней свободы) коэффициент (Adjusted R-squared), имеющий вид

или после преобразования
|
|
|
 .
.
В отличие от  ,
, 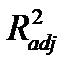 будет убывать, если в уравнение регрессии будут добавляться незначимые независимые переменные (с t-статистикой < 1).
будет убывать, если в уравнение регрессии будут добавляться незначимые независимые переменные (с t-статистикой < 1).
Исправленный коэффициент позволяет избежать переоценки независимой переменной при включении её в уравнение регрессии. Если добавление переменной приводит к увеличению 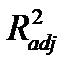 , то включение её в уравнение регрессии оправданно, в противном случае – нет.
, то включение её в уравнение регрессии оправданно, в противном случае – нет.
Продолжим анализ точности уравнения регрессии. Как уже отмечалось, при проверке значимости уравнения регрессии проверяется гипотеза о том, что все коэффициенты модели регрессии равны нулю. Если нулевая гипотеза отклоняется, то это означает, что не все коэффициенты в модели регрессии равны нулю, и тогда встаёт вопрос о проверке значимости каждого параметра регрессии в отдельности.
Такая проверка осуществляется на основе t-статистик, определяемых из соотношений
 , k = 0,1,2,…,m,
, k = 0,1,2,…,m,
где  – выборочные стандартные ошибки соответствующих оценок.
– выборочные стандартные ошибки соответствующих оценок.
Как известно,
 = MSR [(XTX)-1] kk , (k = 0,1,…,m). (2.5)
= MSR [(XTX)-1] kk , (k = 0,1,…,m). (2.5)
Здесь [(XTX)-1]kk – соответствующие диагональные элементы матрицы (XTX)-1 .
При компьютерных расчётах вместе с t-статистикой (t-Statistic) для каждой оценки параметров уравнения регрессии вычисляется выборочный уровень значимости или Prob – это вероятность того, что вычисленное значение t-статистики не превосходит критического значения. По его значению и определяется значимость каждой оценки параметров уравнения регрессии.
|
|
|


