Обобщённый метод наименьших квадратов

При рассмотрении классической регрессионной модели предполагалось, что случайные ошибки не коррелированы между собой и имеют постоянную дисперсию. Однако во многих ситуациях эти предположения не выполняются (не однородные объекты, зависимости во времени и т. п.). В этих случаях ковариационная матрица остатков не имеет вид 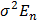, как это предполагалось раньше, а может быть произвольной симметричной положительно определённой матрицей V. С помощью линейного преобразования исходную систему можно свести к обычному регрессионному уравнению и построить для него МНК-оценку вектора коэффициентов. Эта оценка зависит от матрицы ковариаций остатков регрессии, а способ оценивания носит название обобщённого метода наименьших квадратов (ОМНК). Для ОМНК-оценки устанавливается аналог теоремы Гаусса –Маркова, а именно, доказывается, что в классе всех несмещённых линейных оценок она обладает наименьшей матрицей ковариаций (теорема Айткена).

В общем случае оценка параметров уравнения регрессии имеет вид 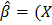^TV^-1X)^-1X^TV^-1Y, где V – ковариационная матрица остатков регрессионной модели. В классическом варианте, когда остатки гомоскедастичны и в них отсутствует какая-либо автокорреляция V = 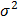E_n, где E_n – единичная матрица размерности nхn, тогда 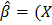^TX)^-1X^TY).

Для применения ОМНК необходимо знать матрицу V, что на практике практически не реально (пришлось бы оценивать n(n – 1)/2 параметров при n наблюдениях). Если каким -либо образом (путём введения каких-либо условий на поведение остатков) удаётся оценить эту матрицу, то естественно использовать её в ОМНК для получения оценок вектора параметров модели. Такой подход составляет суть так называемого доступного ОМНК, одним из вариантов которого является взвешенный МНК.

Взвешенный МНК представляет собой случай, когда ковариационная матрица V является диагональной (отсутствие какой-либо автокорреляции), а на главной диагонали находятся 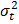(наличие гетероскедастичности). В этом случае иногда возможно представление 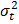= 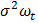, где – некие веса. Особенно это удобно, если остатки уравнения регрессии пропорциональны значениям какой-либо переменной. Тогда в качестве весов можно взять значения этой переменной в выборке. Разделив все переменные анализируемого уравнения, можно применять обычный МНК к преобразованному уравнению. В случае удачного выбора весов можно успешно провести коррекцию на гетероскедастичность остатков уравнения регрессии.

Здесь надо иметь в виду, что после оценки преобразованного уравнения, необходимо будет перейти в коэффициентам исходного уравнения. Например, если исходное уравнение имело вид y = a + b₁x₁ + b₂x₂ + e и выяснилось, что остатки пропорциональны x₁, то преобразованное уравнение примет вид y/x₁ =a(1/x₁) + b₁ + b₂(x₂/x₁) + e/x₁. В последнем уравнении свободный член уравнения (b₁) и коэффициент при x₁ (a) поменялись местами по отношению к исходному уравнению. После применения стандартного МНК к преобразованному уравнению необходимо будет вернуться к обозначениям исходного уравнения, а именно: считать а свободным членом исходного уравнения, а b₁ – коэффициентом при x₁.

 

Пример 3. Взвешенный метод наименьших квадратов

Проиллюстрируем идею взвешенного МНК на следующем примере (В. П. Носко, часть 1, 2011). Для исследования вопроса о зависимости количества руководящих работников от размера предприятия были собраны статистические данные по 27 предприятиям (х – численность персонала, у – количество руководителей).

Уравнение регрессии приведено на рисунке 2.18.

 

 

Рисунок 2.18 – Отчёт об уравнении регрессии зависимости количества руководителей от численности персонала

 

На рисунке 2.19 приведён график остатков для этого уравнения. Видно, что остатки гетероскедастичны. Причём остатки пропорциональны независимой переменной х. кроме того, тест Бройша – Годфри показал наличие в остатках автокорреляции второго порядка (рисунок 2.20).

 

 

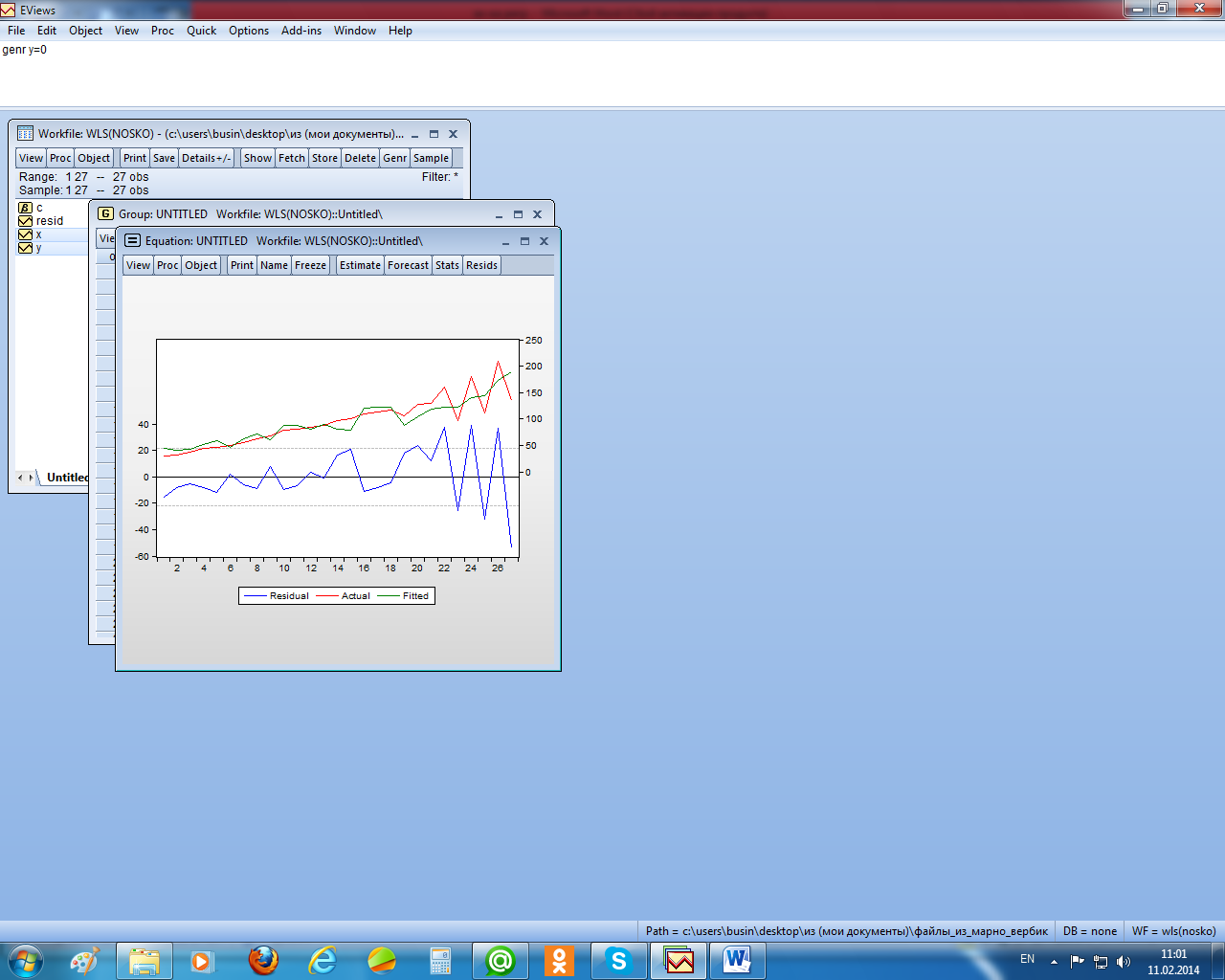
Рисунок 2.19 – График остатков уравнения регрессии

 

 

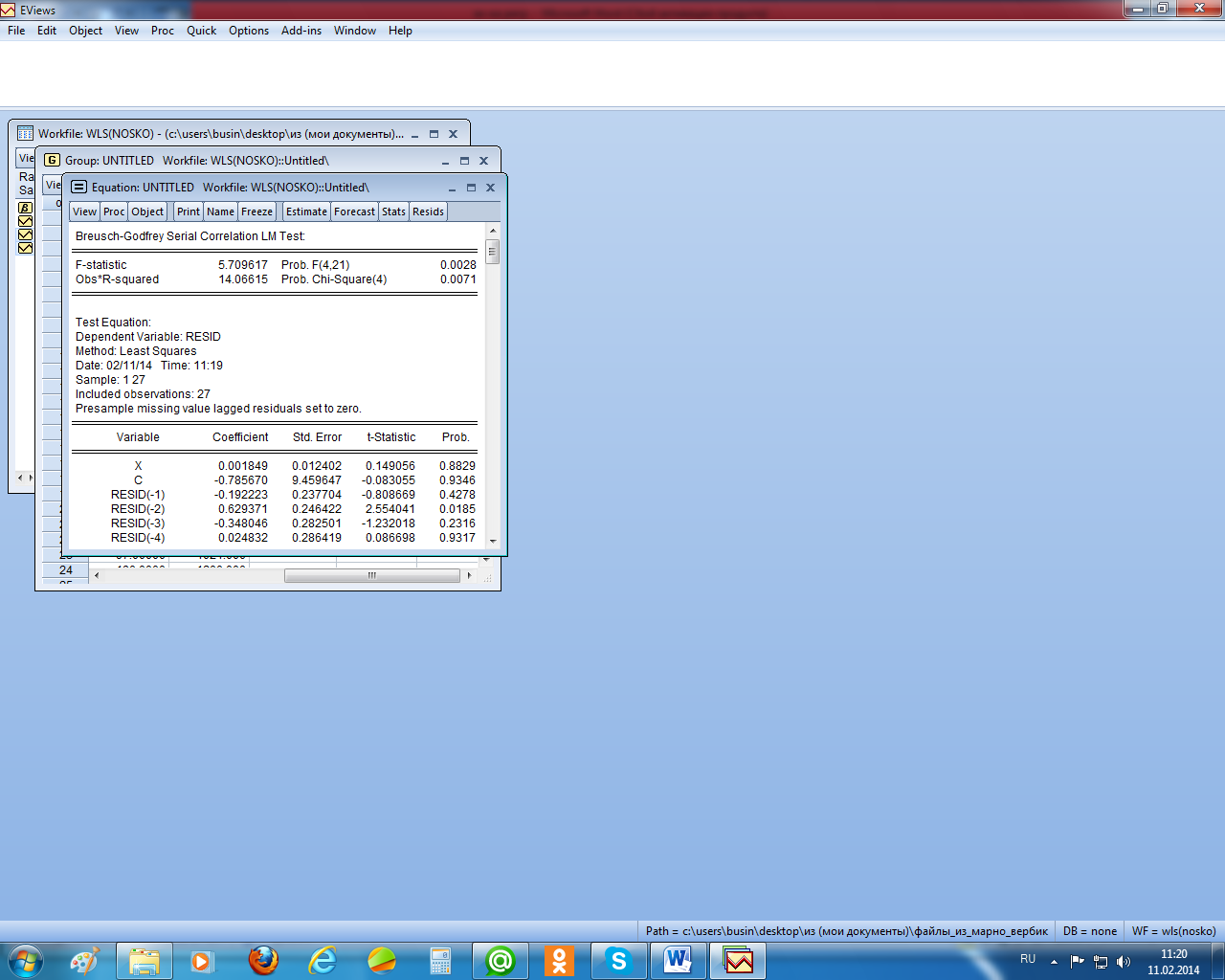
Рисунок 2.20 – Тест Бройша – Годфри на автокорреляцию остатков

 

Поскольку остатки гетероскедастичны и автокоррелированы, проведём коррекцию их стандартных ошибок методом Ньюи – Веста (рисунок 2.21). Как видим, существенного изменения в оценках стандартных ошибках не произошло.

 

 

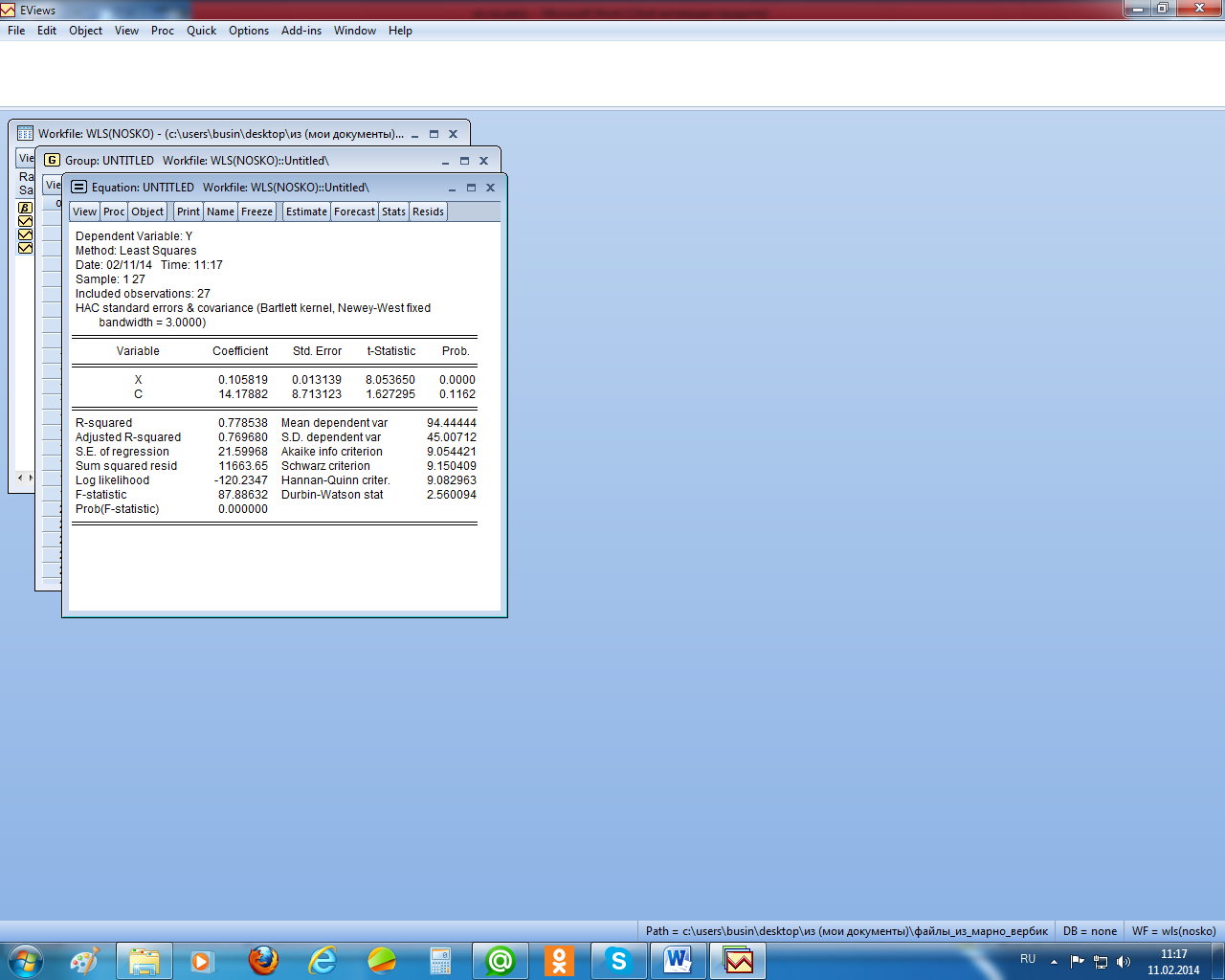
Рисунок 2.21 – Стандартные ошибки в форме Ньюи – Веста

 

Для сравнения с проведённым исследованием применим взвешенный МНК, использовав в качестве весов 1/х, поскольку, как видно из рисунка 2.19, остатки пропорциональны независимой переменной. В результате получили следующее уравнение регрессии (рисунок 2.22).

 

 

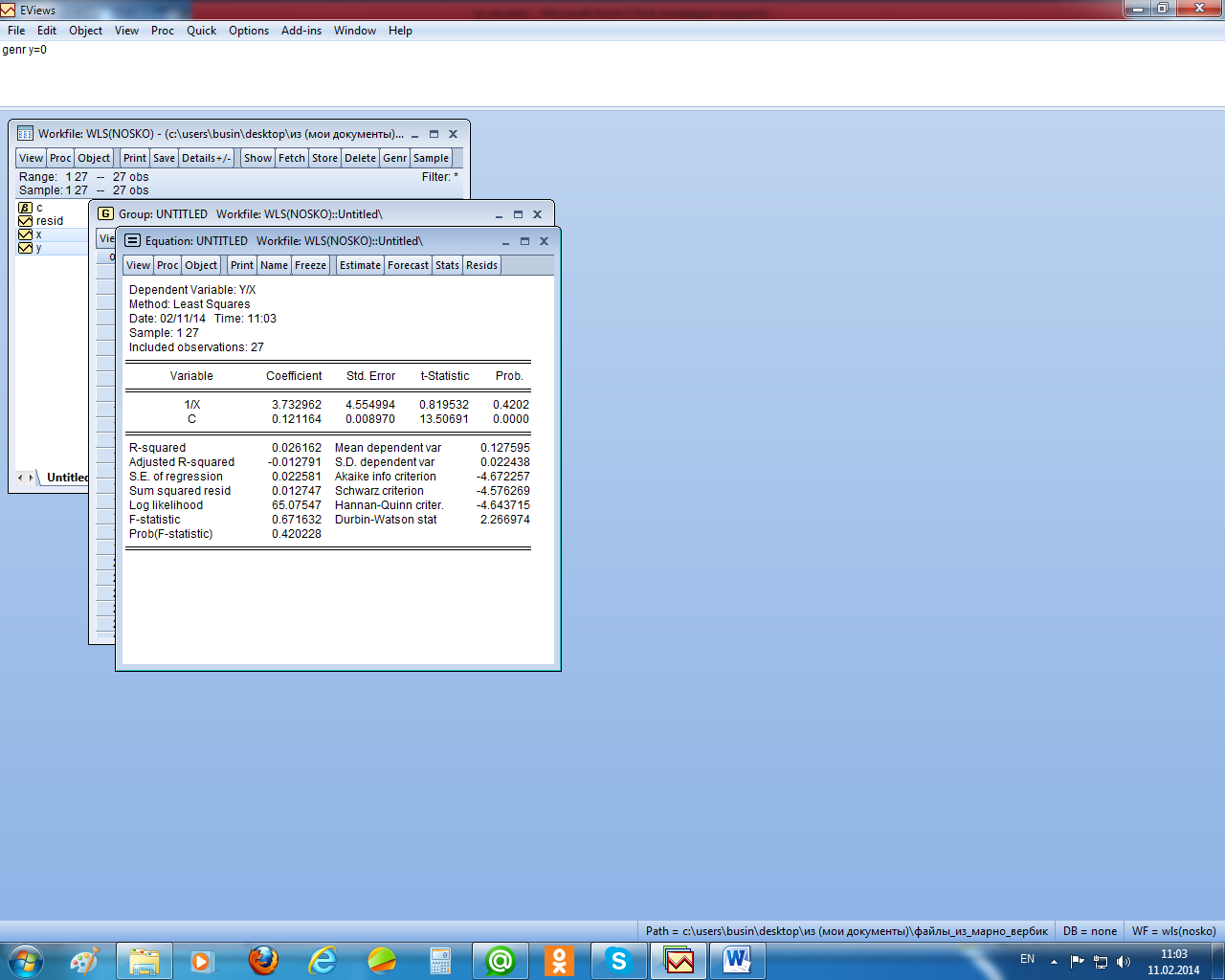
Рисунок 2.22 – Взвешенный МНК

 

Как отмечалось, коэффициенты этого уравнения нужно интерпретировать в рамках исходного уравнения регрессии, т. е. константа – это коэффициент при х в исходном уравнении. Он незначимо отличается от коэффициента в исходной модели. Аналогично можно сказать и об оценке его стандартной ошибки. Различие же в свободных членах здесь не существенно, т. к. эти оценки незначимо отличаются от нуля (и там и там расчётный уровень значимости больше 0,05).

 

 

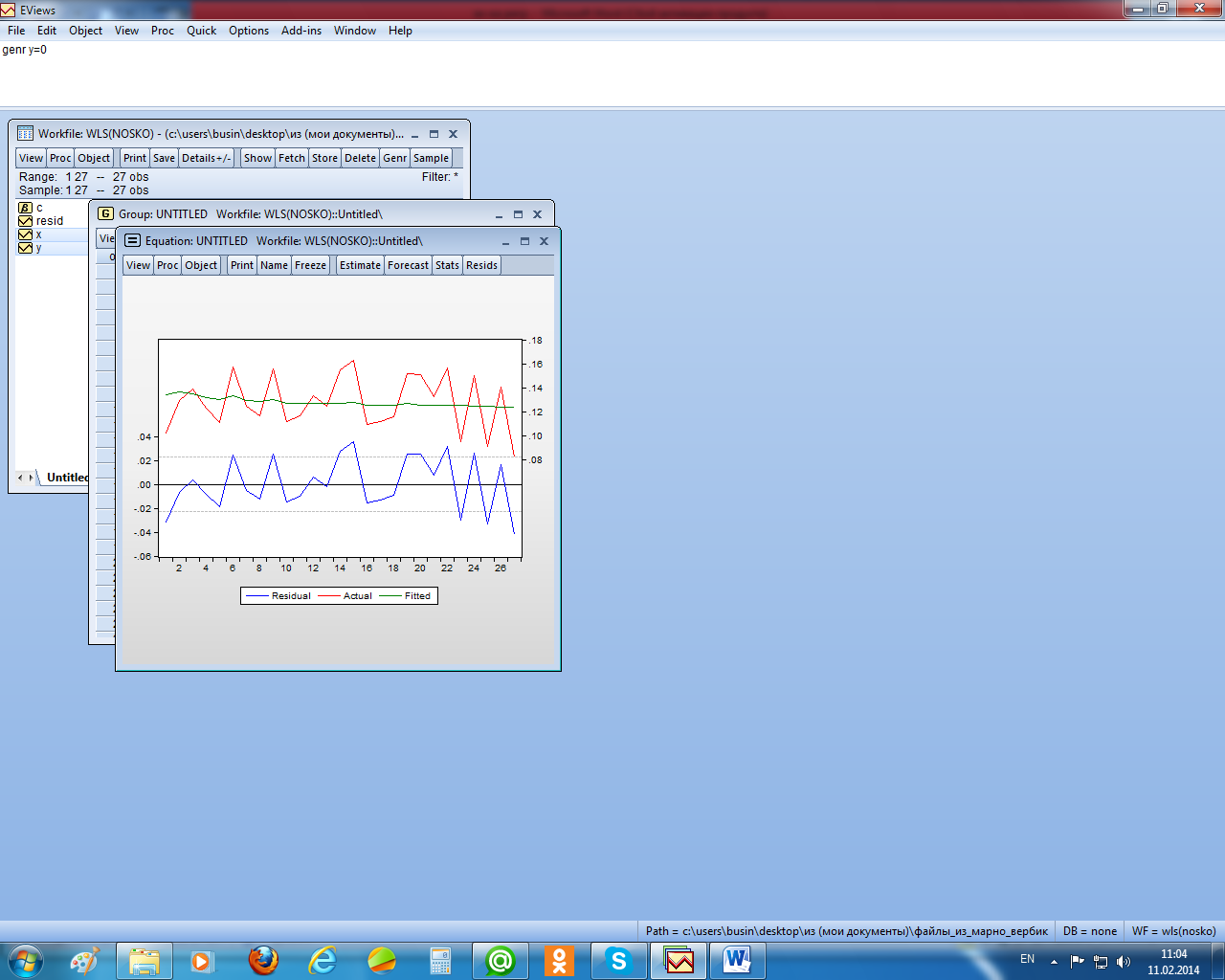
Рисунок 2.23 – График остатков преобразованного уравнения регрессии

 

А вот от гетероскедастичности в остатках этим методом (взвешенным МНК) удалось избавиться, их разброс вокруг нуля стал равномерным (рисунок 2.23).

 

⇐ Предыдущая78910111213141516Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: