 |
Ранжированные переменные, вычисление производных.
|
|
|
|
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ УКРАИНЫ
ВОСТОЧНОУКРАИНСКИЙ НАЦИОНАЛЬНЫЙ
УНИВЕРСИТЕТ ИМ. В. ДАЛЯ
МЕТОДИЧЕСКИЕ УКАЗАНИЯ
по дисциплине
«КОМПЬЮТЕРНАЯ ТЕХНИКА И ПРОГРАМИРОВАНИЕ»
тема: «МАТЕМАТИЧЕСКИЙ ПАКЕТ MATHCAD 11. ЛАБОРАТОРНЫЙ ПРАКТИКУМ»
(для студентов технических специальностей)
У Т В Е Р Ж Д Е Н О
на заседании кафедры
«Компьютерные системы и сети»
Протокол № от
Луганск, ВНУ им. В. Даля, 2007
УДК
Методические указания по дисциплине «Компьютерная техника и програмирование», тема «Математический пакет MathCad 11. Лабораторный практикум» / Сост.: Ю.В. Полупан – Луганск: Изд-во Восточноукр. Нац. ун-та, 2006. – стр.
В методических указаниях изложен перечень лабораторных работ по теме «Математический пакет MathCad 11», приведены образцы выполнения данных работ с подробным объяснением хода решения.
Рассматриваются типы данных, применяемых в документах MathCad, и принципы их ввода-вывода в наиболее простой числовой форме. Приведена методика работы с массивами, которые реализованы в виде векторов и матриц, что максимально приближает стиль вычислений к общепринятой математической форме.
Рассматриваются возможности символьного процессора MathCad 11, что позволяет решить многие задачи математики аналитически, без применения численных методов и, соответственно, без погрешностей вычислений.
Так же в методических указаниях разработаны лабораторные работы, в которых рассматривается решение алгебраических нелинейных уравнений и систем таких уравнений.
Составители: О.С. Петров, проф.,
Ю.В. Полупан, асс.
Отв. за выпуск: Петров А.С.
Рецензент:
Методические указания представляют MathCad 11, перечень лабораторных работ, предназначенных для выполнения в математическом пакете MathCad 11, с подробным описанием решения данных задач. При этом в качестве примеров применения системы MathCad 11 взяты расчеты, наиболее часто встречающиеся при решении типовых задач в курсе «Высшая математика» университетов и вузов.
|
|
|
ЛАБОРАТОРНАЯ РАБОТА №1
Решение систем линейных уравнений методом Крамера, обратной матрицы и методом Жордана-Гаусса. Векторная алгебра.
Задача I.
Решить заданную систему уравнений, пользуясь формулами Крамера, методом обратной матрицы и методом Жордана-Гаусса.
x - 2y + 3z = 6;
2x + 3y - 4z = 16;
3x - 2y - 5z = 12
Выполнение:
Метод Крамера
1) Изначально необходимо ввести матрицу системы и матрицу свободных членов. Для данного случая:
 – матрица системы;
– матрица системы;
 – матрица свободных членов.
– матрица свободных членов.
а) Для ввода матрицы А щелкните в том месте рабочего окна, в котором хотите создать матрицу A. Введите обозначение А и оператор:=. Вызовите на экран панель инструментов (Матрицы) с помощью последовательности команд: меню Вид - Панели инструментов - Матрицы. Окно имеет вид, изображенный на рис. 1.

Рис. 1.
Активизируйте кнопку под названием (Создать матрицу или вектор). В появившемся диалоговом окне (рис. 2) введите количество строк (Rows) и количество столбцов (Columns) для создаваемой матрицы А. В вашем случае количество строк 3, количество столбцов 3.

Рис. 2.
После выполненных действий в рабочем окне документа появится матрица, в которую необходимо ввести коэффициенты при неизвестных. При введении коэффициентов можно использовать клавишу Tab.
б) Для ввода вектора В щелкните в том месте рабочего окна, в котором хотите создать вектор В. Введите обозначение В и оператор:=. Вызовите на экран панель инструментов (Матрицы) (в том случае, если она па экране отсутствует) с помощью последовательности команд: меню Вид - Панели инструментов - Матрицы. Окно имеет вид, изображенный на рис. 1.
|
|
|
Активизируйте кнопку под названием (Создать матрицу или вектор). В появившемся диалоговом окне (рис. 2) введите количество строк (Rows) и количество столбцов (Columns) для создаваемого вектора В. В нашем случае количество строк 3, количество столбцов 1.
После выполненных действий в поле рабочего документа появится вектор-столбец, вкоторый необходимо ввести коэффициенты при свободных членах решаемой системы. При введении коэффициентов можно использовать клавишу Tab.
2) Вычислим определитель матрицы А. Для этого следует щелкнуть в том месте рабочего листа, где планируется поместить определитель. Щелкните на кнопке (Вычисление определителя) наборной панели (Матрицы). В пустой местозаполнитель  появившейся записи внесите имя матрицы |А| и активизируйте клавишу =.
появившейся записи внесите имя матрицы |А| и активизируйте клавишу =.
Полученная запись будет иметь вид: |А| = и появится значение определителя матрицы А. Если определитель равен 0, то данная система имеет больше одного решения и не имеет смысла дальнейшее её решение. Если определитель не равен 0, то система имеет единственное решение, которое может быть определено с помощью метода Крамера.
3) Введите матрицы А1, А2, A3 аналогично матрице А. Матрица А1 получается из матрицы А заменой первого столбца в матрице А на столбец свободных членов В, то есть для данной системы имеем:
 .
.
Матрица А2 получается из матрицы А заменой второго столбца в матрице А на столбец свободных членов В, то есть для данной системы имеем:

Матрица A3 получается из матрицы А путем замены третьего столбца на столбец свободных членов В. Матрицу А3 сформировать самостоятельно.
4) Вычислите определители матриц Al, A2, A3. Для этого установите курсор в ту область рабочего листа, где хотите вычислить определитель и активизируйте кнопку (Вычисление определителя) (рис. 1). Создайте запись  =. Аналогично вычислите определители матриц А2 и A3 создав записи
=. Аналогично вычислите определители матриц А2 и A3 создав записи 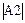 = и
= и  =.
=.
5) Далее, согласно методу Крамера, создайте формулы для вычисления переменных х, у, z и вычислите их.
Формула для вычисления перемененной х:  . Для определения непосредственно значения переменной х, установите курсор правее или ниже данной формулы и напишите х=.
. Для определения непосредственно значения переменной х, установите курсор правее или ниже данной формулы и напишите х=.
|
|
|
Формула для вычисления у:  . Для определения непосредственно значения переменной у, установите курсор правее или ниже данной формулы и напишите у=.
. Для определения непосредственно значения переменной у, установите курсор правее или ниже данной формулы и напишите у=.
Формула для вычисления z:  . Для определения непосредственно значения переменной z установите курсор правее или ниже данной формулы и напишите z=.
. Для определения непосредственно значения переменной z установите курсор правее или ниже данной формулы и напишите z=.
Матричный метод
1) При решении системы линейных уравнений данным методом ответом будет являться вектор-столбец, который будет состоять из значений переменных х, у, z, при которых данная система преобразуется в тождество.
2) Для решения системы матричным методом запишите формулу решения системы матричным методом. Формула для данного случая имеет вид:  , где R - вектор-столбец, состоящий из значений решения системы. Для получения значений искомых переменных установите курсор правее или ниже данной формулы и напишите R=.
, где R - вектор-столбец, состоящий из значений решения системы. Для получения значений искомых переменных установите курсор правее или ниже данной формулы и напишите R=.
Получим:




3) Решение будет иметь вид  . Это значит, что x=7, y=2, z=1. Значения переменных x, y, z, полученные матричным методом, должны быть в точности равны значениям этих перемнных, полученных методом Крамера. Если значения не совпадают, знпачит, в ходе решения либо по методу Крамера либо по методу обратной матрицы были допущены ошибки.
. Это значит, что x=7, y=2, z=1. Значения переменных x, y, z, полученные матричным методом, должны быть в точности равны значениям этих перемнных, полученных методом Крамера. Если значения не совпадают, знпачит, в ходе решения либо по методу Крамера либо по методу обратной матрицы были допущены ошибки.
Метод Жордана -Гаусса
1) При решении системы линейных уравнений данным методом ответом будет являться вектор-столбец, который будет состоять из значений переменных x, y, z при которых данная система переобразуется в тождество.
2) Для решения системы методом Жордана-Гаусса запишите формулу, включающую функцию lsolve. Если переменная А обозначает систему, а переменная В обозначает матрицу свободных членов, то данная формула запишется следующим образом:  . Для получения значений искомых переменных установите курсор правее или ниже данной формулы и напишите
. Для получения значений искомых переменных установите курсор правее или ниже данной формулы и напишите  . Получим:
. Получим:




3) Значения переменных x, y, z, полученные методом Жордана-Гаусса, должны быть в точности равны значениям этих перемнных, полученных методом Крамера и методом обратной матрицы. Если значения не совпадают, значит, в ходе решения либо по методу Крамера либо по методу обратной матрицы были допущены ошибки.
|
|
|
Задача II.
Даны координаты вершин А1=(2, -3, 5), А2=(0,2,1), А3=(-2,-2,3), А4=(3,2,4). Средствами векторной алгебры найти:
а) длину ребра А1А2;
б) угол между ребрами А1А2 и А1А3;
в) площадь грани А1А2А3;
г) объём пирамиды А1А2А3А4;
д) высоту пирамиды.
Выполнение:
Введите векторы-столбцы А1, А2, А3, А4 в следующем виде:




а) Для нахождения длины ребра А1А2 необходимо определить этот вектор. Согласно векторной алгебре записываем формулу для определения самого вектора: А1А2:=А2-А1. Для определения длины вектора А1А2 с помощью наборной панели матрицы создайте запись:  . Ответ будет получен автоматически и равен
. Ответ будет получен автоматически и равен  6.708. Для дальнейших вычислений определим вектора А1А3 и А1А4 как
6.708. Для дальнейших вычислений определим вектора А1А3 и А1А4 как
А1А3:=А3-А1
А1А4:=А4-А1
б) Угол между ребрамии определим по формуле известной из курса векторной алгебры:

Для вывода результата, вычисленного по формуле, левее или ниже данной формула запишите 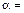 .
.
в) Площадь грани А1А2А3 находим по следующей формуле:

г) Объём пирамиды находим по следующей формуле:

д) Высоту пирамиды вычислим по формуле: 
ВЫПОЛНИТЬ САМОСТОЯТЕЛЬНО
Задача 1.
Постановка задачи: Решить две системы линейных уравнений методом Крамера, Матричным методом и методом Жордана-Гаусса.
1. В математической системе MathCad создать файл и занести в него условие задачи в соответствии с вариантом (таблица 1). Вариант выбирается по номеру в списке журнала. Сохранить файл под именем «СЛУ-Фамилия».
2. Решить систему линейных уравнений тремя методами. Получить результат в дробном и вещественном виде.
Т а б л и ц а 1.
Варианты заданий
| № варианта | Система | № варианта | Система |
| x1-x2+2x3 =2 3x1+x2-x3 =3 4x1-x2-5x3 =-2 x1+8x2-5x3=-7 3x1+2x2+x3=1 2x1-3x2+2x3=9 | 6x1+6x2+2x3=-11 11x1+9x2+2x3=-22 4x1+5x2+2x3=-5 12x1+6x2+x3=5 19x1+16x2+7x3=256 x1+ x2 =-2 | ||
| 3x1-3x2-4x3=-1 6x1-6x2+x3=0 4x1-9x2-2x3=-3 3x1+4x2+7x3=1 -2x1+5x2-3x3=1 5x1-6x2+11x3=-3 | 4x1+3x2+2x3=1 4x1+5x2+2x3=3 3x1+2x2+3x3=5 6x1+9x2+4x3=-8 -x1-x2+x3=2 10x1+16x2+7x3=-15 | ||
| 2x1-x2-x3=4 3x1+4x2-2x3=11 3x1-2x2+4x3=11 2x1+x2-x3=-1 2x1-x2+2x3=-4 4x1+x2+4x3=-2 | x1+x2+x3=-1 3x1+4x2+3x3=-6 9x1+8x2+5x3=-10 -x1+3x2-2x3=2 2x1-x2+3x3=1 2x1-3x2+4x3=-1 | ||
| x1+2x2-2x3=-3 2x1+x2-2x3=0 3x1+x2+4x3=6 x1+2x2+3x3=5 x1+3x2+2x3=1 3x1+x2+2x3=11 | 3x1+2x2+2x3=-1 2x1+5x2+3x3=-6 3x1+4x2+4x3=-5 2x1+4x2+3x3=0 x1+5x2+4x3=-3 -3x1+5x2+3x3=-11 | ||
| 4x1+x2+2x3=-2 -x1+2x2+3x3=5 -2x1+3x2+x3=8 4x1+2x2+x3=31 2x1+x2+5x3=29 x1-x2+3x3=10 | 2x1+2x2+x3=2 3x1+3x2+x3=1 2x1-x2 =8 x1+3x2+5x3=-8 x1+4x2+8x3=-15 x1+2x2+6x3=-13 | ||
| 6x1+7x2+3x3=2 3x1+x2-2x3=2 2x1+2x2+x3=1 9x1+9x2+5x3=2 4x1-x2-2x3=-5 14x1+13x2+7x3=-1 | 2x1-4x2+9x3=28 7x1+3x2-6x3=-1 7x1+9x2-9x3=5 x1+x2-x3=36 x1-x2+x3=13 x1-x2-x3=-7 | ||
| -2x1+3x2+4x3=5 3x1-x2-3x3=-1 -x1+2x2+2x3=3 3x1+3x2+x3=8 7x1+6x2+2x3=18 7x1+9x2+2x3=21 | x1+2x2+x3=4 3x1-5x2+3x3=1 2x1+7x2-x3=8 7x1+2x2+3x3=15 5x1-3x2+2x3=15 10x1-11x2+5x3=36 | ||
| 15. | 9x1+7x2+3x3=-10 14x1+9x2+4x3=-15 3x2+2x3=5 4x1+2x2+x3=31 2x1+x2+5x3=29 x1-x2+3x3=10 | 16. | x1+x2+x3=36 2x1 -3x3=-17 6x1 -5x3=7 2x1-4x2+9x3=28 7x1+3x2-6x3=-1 7x1+9x2-9x3=5 |
| 3x1-3x2-4x3=-1 6x1-6x2+x3=0 4x1-9x2-2x3=-3 x1+x2+x3=-1 3x1+4x2+3x3=-6 9x1+8x2+5x3=-10 | 3x1+4x2+7x3=1 -2x1+5x2-3x3=1 5x1-6x2+11x3=-3 x1+2x2-2x3=-3 2x1+x2-2x3=0 3x1+x2+4x3=6 | ||
| x1+2x2+3x3=5 x1+3x2+2x3=1 3x1+x2+2x3=11 6x1+7x2+3x3=2 3x1+x2-2x3=2 2x1+2x2+x3=1 | 2x1+4x2+3x3=0 x1+5x2+4x3=-3 -3x1+5x2+3x3=-11 x1+2x2+x3=4 3x1-5x2+3x3=1 2x1+7x2-x3=8 |
Задача 2.
|
|
|
Постановка задачи: Даны координаты вершин ABCD. средствами векторной алгебры найти: а) длину ребра AB; б) угол между рёбрами AB и AC; в) площадь грани ABCD; объём пирамиды ABCD; г) высоту пирамиды ABCD.
В математической системе MathCad создать файл и решить в нем поставленную задачу в соответствии с вариантом (таблица. 2). Вариант выбирается по номеру в списке журнала. Сохранить файл под именем «Пирамида-Фамилия». Где возможно, получить результат в дробном и вещественном виде. Сохранить файл «Пирамида-Фамилия» локально на диске.
Задача 3.
Постановка задачи: Даны точки A, B, C, D. Положим а =  , b =
, b = 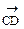 . Найти:
. Найти:
а) векторы 2а+b и а-2b;
б) модули векторов |2а+b| и |а-2b|;
в) скалярное произведение (2а+b)×(a-2b);
г) векторное произведение [(2а+b),(a-2b)];
д) угол между векторами (2а+b)×и (a-2b).
В математической системе MathCad создать файл и решить в нем поставленную задачу в соответствии с вариантом (таблица. 2). Вариант выбирается по номеру в списке журнала. Сохранить файл под именем «Векторы-Фамилия». Где возможно, получить результат в дробном и вещественном виде. Сохранить файл «Векторы-Фамилия» локально диске.
Т а б л и ц а 2.
Варианты заданий
| 1. | A(1,0,2) | B(-1,2,3) | C(2,3,1) | D(-3,4,5,) |
| 2. | A(0,3,-2) | B(4,1,3) | C(-1,1-1) | D(3,2,4) |
| 3. | A(-1,-1,0) | B(1,1,1) | C(-2,1,0) | D(0,-2,7) |
| 4. | A(0,2,0) | B(-2,0,0) | C(3,1,0) | D(0,-1,-3) |
| 5. | A(2,1,-1) | B(-1,-3,-1) | C(0,-1-1) | D(2,4,1) |
| 6. | A(2,2,-1) | B(0,0,0) | C(0,-4,0) | D(2,0,0) |
| 7. | A(-3,2,4) | B(-3,-3,4) | C(0,-3,4) | D(-1,-1,4) |
| 8. | A(5,6,1) | B(6,1,4) | C(1,2,3) | D(2,0,2) |
| 9. | A(-5,6,0) | B(-6,-2,1) | C(-3,4,-1) | D(-1,-7,0) |
| 10. | A(10,9,0) | B(9,8,1) | C(8,7,1) | D(7,6,0) |
| 11. | A(7,7,0) | B(5,6,0) | C(4,5,1) | D(3,4,1) |
| 12. | A(-5,-2,0) | B(-3,-3,1) | C(0,5,0) | D(9,6,1) |
| 13. | A(-1,0,-1) | B(1,1,-1) | C(1,2,-3) | D(0,-2,-4) |
| 14. | A(1,6,2) | B(-1,0,1) | C(4,2,3) | D(-1,-1,4) |
| 15. | A(3,6,4) | B(3,5,3) | C(2,4,2) | D(1,0,1) |
| 16. | A(7,2,7) | B(9,1,7) | C(9,7,6) | D(-1,-1,7) |
| 17. | A(4,-3,2) | B(1,-7,2) | C(-1,0,1) | D(1,1,1) |
| 18. | A(0,-5,3) | B(2,2,2) | C(0,-3,1) | D(7,7,2) |
| 19. | A(1,6,7) | B(0,6,7) | C(-4,5,6) | D(-4,-4,8) |
| 20. | A(2,1,-1) | B(-1,-3,-1) | C(0,-1-1) | D(2,4,1) |
ЛАБОРАТОРНАЯ РАБОТА №2.
Ранжированные переменные, вычисление производных.
Дана функция  .
.
а) найти первую производную функции f(x) и обозначить её через  . Привести первую производную к одному знаменателю;
. Привести первую производную к одному знаменателю;
б) найти вторую производную функции f(x) и обозначить её через  . Привести вторую производную к одному знаменателю;
. Привести вторую производную к одному знаменателю;
в) вычислить значение первой и второй производной в интервале [4;5] с шагом 0.2;
г) найти сумму:
–  в качестве слагаемых которой будут служить значения функции
в качестве слагаемых которой будут служить значения функции  , вычисленной в каждой точке интервала ранжированной переменной;
, вычисленной в каждой точке интервала ранжированной переменной;
– 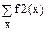 в качестве слагаемых которой будут служить значения функции
в качестве слагаемых которой будут служить значения функции  , вычисленной в каждой точке интервала ранжированной переменной;
, вычисленной в каждой точке интервала ранжированной переменной;
–  в качестве слагаемых которой будут служить сумма значений функций
в качестве слагаемых которой будут служить сумма значений функций  и
и  , вычисленных в каждой точке интервала ранжированной переменной;
, вычисленных в каждой точке интервала ранжированной переменной;
д) найти произведение:
–  в качестве аргументов которого будут служить значения функции
в качестве аргументов которого будут служить значения функции  , вычисленной в каждой точке интервала ранжированной переменной;
, вычисленной в каждой точке интервала ранжированной переменной;
–  в качестве аргументов которого будут служить значения функции
в качестве аргументов которого будут служить значения функции  , вычисленной в каждой точке интервала ранжированной переменной;
, вычисленной в каждой точке интервала ранжированной переменной;
–  в качестве аргументов которой будет служить сумма значений функций
в качестве аргументов которой будет служить сумма значений функций  и
и  , вычисленных в каждой точке интервала ранжированной переменной;
, вычисленных в каждой точке интервала ранжированной переменной;
е) на одном графике построить графики функций  .
.
ВЫПОЛНЕНИЕ:
а) Зададим функцию  в виде:
в виде:

Знак суммы «+» и разности «-» ставится после дроби следующим образом:
– установите курсор в знаменатель дроби, например  и активизируйте клавишу «Пробел»;
и активизируйте клавишу «Пробел»;
– после того как курсор будет помещен после дроби, выделив её при этом  , активизируйте клавишу «+».
, активизируйте клавишу «+».
б) Для нахождения первой производной воспользуемся панелью инструментов «Вычисления» (Матанализ), рис. 3.

Рис. 3.
Получим выражение первой производной в виде, рис. 4:

Рис. 4.
Присвоим функции  выражение первой производной функции
выражение первой производной функции  рис 5:
рис 5:

Рис. 5.
Для того, чтобы привести функцию  к одному знаменателю, выделим выражение, которое необходимо привести к одному знаменателю (рис. 6) и выполним последовательность действий меню Символы-Упростить.
к одному знаменателю, выделим выражение, которое необходимо привести к одному знаменателю (рис. 6) и выполним последовательность действий меню Символы-Упростить.

Рис. 6.
После выполнения данной последовательности действий ниже выделенного выражения появиться то же выражение, но приведенное к одному знаменателю рис. 7.

Рис. 7.
в) Для нахождения второй производной аналогично воспользуемся панелью инструментов «Вычисления» (Матанализ), но кнопкой «Производная n-ого порядка» (рис. 8)

Рис. 8.
Получим выражение второй производной в виде, рис. 9:

Рис. 9.
Присвоим функции  выражение второй производной функции
выражение второй производной функции  рис. 10:
рис. 10:

Рис. 10.
 Для приведения функции
Для приведения функции  к одному знаменателю выполним последовательность действий, указанную в пункте (б).
к одному знаменателю выполним последовательность действий, указанную в пункте (б).
г) Для вычисления значений первой и второй производной в интервале [4; 5] с шагом h=0.2 сначала необходимо определить значения переменной x на данном интервале, то есть определить переменную x как ранжированную переменную. Общий вид ранжированной переменной следующий:
имя_переменной:=
начальное_значение_интервала,(начальное_значение_интервала+
+шаг)..(конечное_значение_интервала)
В нашем случае:
имя_переменной – x;
начальное_значение_интервала=a=4; шаг=h=0.2; конечное_значение_интервала=b=5.
Таким образом, чтобы определить ранжированную переменную x в соответствии с условием задачи необходимо в MathCad создать следующую запись (рис. 11):
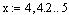
Рис. 11.
Теперь можно вычислить значения первой и второй производной функции  , то есть значения функций
, то есть значения функций  и
и  соответственно, а также вывести на экран значения переменной x. Для этого достаточно создать следующую запись (рис. 12).
соответственно, а также вывести на экран значения переменной x. Для этого достаточно создать следующую запись (рис. 12).

|
д) После того как значения функций  и
и  определены на заданном интервале с шагом h, можно найти сумму:
определены на заданном интервале с шагом h, можно найти сумму:


Для нахождения суммы  воспользуемся панелью инструментов «Вычисления» (Матанализ), рис. 13.
воспользуемся панелью инструментов «Вычисления» (Матанализ), рис. 13.
 |

Рис. 13.
Активизируем кнопку «Сумматор ранжированных переменных» и создадим запись рис. 14:

Рис. 14.
Значение суммы расчитывается автоматически после того, как будет поставлен с помощью клавиатуры знак равенства «=». Значение суммы 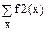 рассчитывается аналогично.
рассчитывается аналогично.
Для нахождения суммы  необходимо создать запись рис. 15:
необходимо создать запись рис. 15:

Рис. 15.
После того как значения функций  и
и  определены на заданном интервале с шагом h, можно найти произведение:
определены на заданном интервале с шагом h, можно найти произведение:


Для нахождения произведения  воспользуемся панелью инструментов «Вычисления» (Матанализ), рис. 16.
воспользуемся панелью инструментов «Вычисления» (Матанализ), рис. 16.


Рис. 16.
Активизируем кнопку «Произведение ранжированных переменных» и создадим запись рис. 17:

Рис. 17.
Значение произведения расчитывается автоматически после того, как будет поставлен с помощью клавиатуры знак равенства «=». Значение произведения  и
и  рассчитывается аналогично.
рассчитывается аналогично.
ВЫПОЛНИТЬ САМОСТОЯТЕЛЬНО
Постановка задачи: Дана функция f(x) (таблица 3). Выполнить:
а) найти первую производную функции f(x) и обозначить её через  . Привести первую производную к одному знаменателю;
. Привести первую производную к одному знаменателю;
б) найти вторую производную функции f(x) и обозначить её через  . Привести вторую производную к одному знаменателю;
. Привести вторую производную к одному знаменателю;
в) вычислить значение первой и второй производной на указанном интервале с указанным шагом;
г) найти сумму:
–  в качестве слагаемых которой будут служить значения функции
в качестве слагаемых которой будут служить значения функции  , вычисленной в каждой точке интервала ранжированной переменной х;
, вычисленной в каждой точке интервала ранжированной переменной х;
– 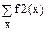 в качестве слагаемых которой будут служить значения функции
в качестве слагаемых которой будут служить значения функции  , вычисленной в каждой точке интервала ранжированной переменной х;
, вычисленной в каждой точке интервала ранжированной переменной х;
–  в качестве слагаемых которой будут служить сумма значений функций
в качестве слагаемых которой будут служить сумма значений функций  и
и  , вычисленных в каждой точке интервала ранжированной переменной х;
, вычисленных в каждой точке интервала ранжированной переменной х;
д) найти произведение:
–  в качестве аргументов которого будут служить значения функции
в качестве аргументов которого будут служить значения функции  , вычисленной в каждой точке интервала ранжированной переменной;
, вычисленной в каждой точке интервала ранжированной переменной;
–  в качестве аргументов которого будут служить значения функции
в качестве аргументов которого будут служить значения функции  , вычисленной в каждой точке интервала ранжированной переменной;
, вычисленной в каждой точке интервала ранжированной переменной;
–  в качестве арнументов которой будут служить сумма значений функций
в качестве арнументов которой будут служить сумма значений функций  и
и  , вычисленных в каждой точке интервала ранжированной переменной;
, вычисленных в каждой точке интервала ранжированной переменной;
е) на одном графике построить графики функций  .
.
В математической системе MathCad создать файл и решить в нем поставленную задачу в соответствии с вариантом (таблица 3). Вариант выбирается по номеру в списке журнала. Сохранить файл под именем «Переменные-Фамилия» локально на диске.
Т а б л и ц а 3.
Варианты заданий
| № варианта | Функция | Интервал | Шаг | ||

| [15;40] | 0.5 | |||

| [25;40] | 0.2 | |||
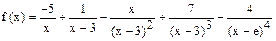
| [-10;-5] | 0.1 | |||

| [8;28] | 0.4 | |||

| [20;35] | 0.2 | |||
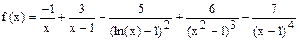
| [-15;35] | 0.2 | |||

| [5;40] | 0.4 | |||
| 8. | 
| [15;36] | 0.3 | ||

| [10;40] | 0.3 | |||

| [-40;-10] | 0.3 | |||

| [-5;-30] | 0.2 | |||

| [2;8] | 0.1 | |||
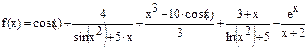
| [2;7] | 0.15 | |||
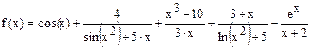
| [-5;-25] | 0.5 | |||

| [3;20] | 0.4 | |||
ЛАБОРАТОРНАЯ РАБОТА №3.
|
|
|


