 |
Решение уравнений и систем нелинейных уравнений. Построение графиков в полярных системах координат.
|
|
|
|
Задача I.
Найти точки пересечения графиков 2-ух функций на интервале [-4; 10]:

ВЫПОЛНЕНИЕ:
а) Решим данную задачу с помощью встроенной в MathCad функции root.
Для этого изобразим поведение данных функций на графике (рис. 32).

Рис. 32.
Для решения данной задачи необходимо найти значение функций в точках (x1,y1), (x2,y2), (x3,y3), (x4,y4), (x5,y5).
Так как в точках пересечения функции y1(x) и y2(x) имеют одинаковое значение, то для нахождения искомых точек можно написать следующее равенство:
 ,
,
или
 .
.
График функции f(x) изображен на рис. 1. В конечном итоге необходимо решить следующее уравнение:
 .
.
Установим приближенные значения искомых корней. Для нахождения точки (x1,y1) возьмем приближенное значение корня x=-3. Получим:
|
|
 .
.
Для нахождения точки (x2,y2) возьмем приближенное значение корня x=0. Получим:
|
|
 .
.
Для нахождения точки (x3,y3) возьмем приближенное значение корня x=3. Получим:
|
|
 .
.
Для нахождения точки (x4,y4) возьмем приближенное значение корня x=7. Получим:
|
|
 .
.
Для нахождения точки (x5,y5) возьмем приближенное значение корня x=8. Получим:
|
|
 .
.
б) Решим данную задачу с помощью блока Given … Find.
Для этого определим точки приближения (приближенные значения корней). Для нахождения точки (x1,y1) установим начальное приближение x=-3, y=0;
|
|

Для нахождения точки (x2,y2) установим начальное приближение x=0, y=0;
|
|

Для нахождения точки (x3,y3) установим начальное приближение x=3, y=2;
|
|

Для нахождения точки (x4,y4) установим начальное приближение x=7, y=3;
|
|

Для нахождения точки (x5,y5) установим начальное приближение x=8, y=4;
|
|

Задача IІ.
|
|
|
Построить графики функции в полярных координатах, зависящих от угла W на интервале  :
:
 ,
,  .
.
ВЫПОЛНЕНИЕ:
Для начала с помощью ранжирования переменной зададим интервал существования W с шагом  . Для этого создадим в MathCad следующую запись:
. Для этого создадим в MathCad следующую запись:  , где 0 – начальное значение интервала;
, где 0 – начальное значение интервала;  – шаг;
– шаг;  – конечное значение интервала.
– конечное значение интервала.
Далее определим сами функции и построим график в полярных координатах (рис. 33).

Рис. 33.
Задача IІІ.
Построить график функции R1(W) в полярных координатах, зависящий от функции R2(W) на интервале  :
:
 ,
,  .
.
ВЫПОЛНЕНИЕ:
Для начала с помощью ранжирования переменной зададим интервал существования W с шагом  . Для этого создадим в MathCad следующую запись:
. Для этого создадим в MathCad следующую запись:
 ,
,
где 0 – начальное значение интервала;  – шаг;
– шаг;  – конечное значение интервала.
– конечное значение интервала.
Далее определим сами функции и построим график в полярных координатах (рис. 34).
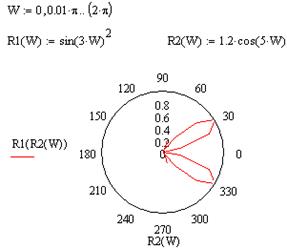
Рис. 34.
ВЫПОЛНИТЬ САМОСТОЯТЕЛЬНО
Задача 1.
а) Постановка задачи: с помощью функции root найти точки пересечения графиков 2-ух функций на указанном интервале (табл. 5). Номер варианта выбрать в соответствии с номером в списке журнала.
В математической системе MathCad создать файл и решить в нем поставленную задачу в соответствии с вариантом (таблица 5). Сохранить файл под именем «root-Фамилия» локально на диске.
б) Постановка задачи: c помощью блока Given…Find найти точки пересечения графиков 2-ух функций на указанном интервале (табл. 5). Номер варианта выбрать в соответствии с номером в списке журнала.
В математической системе MathCad создать файл и решить в нем поставленную задачу в соответствии с вариантом (таблица 5). Сохранить файл под именем «Given-Фамилия» локально на диске.
Т а б л и ц а 5.
Варианты заданий
| № варианта | Система |
Система №1
 Система №2
Система №2

| |
Система №1
 Система №2
Система №2

| |
Система №1
 Система №2
Система №2

| |
Система №1
 Система №2
Система №2

| |
Система №1
 Система №2
Система №2

| |
Система №1
 Система №2
Система №2

| |
Система №1
 Система №2
Система №2

| |
Система №1
 Система №2
Система №2

| |
Система №1
 Система №2
Система №2

| |
Система №1
 Система №2
Система №2

| |
Система №1
 Система №2
Система №2

| |
Система №1
 Система №2
Система №2
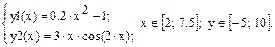
| |
Система №1
 Система №2
Система №2

| |
Система №1
 Система №2
Система №2

| |
Система №1
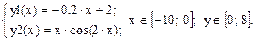 Система №2
Система №2

|
Задача 2.
|
|
|
Постановка задачи: построить графики функций в полярных координатах, зависящих от угла w на указанном интервале (табл. 6). Номер варианта выбрать в соответствии с номером в списке журнала.
В математической системе MathCad создать файл и решить в нем поставленную задачу в соответствии с вариантом (таблица 6). Сохранить файл под именем «Полярные1-Фамилия» локально на диске.
Т а б л и ц а 6.
Варианты заданий
| № варианта | Функции | Шаг | Интервал |


| 0,01 | 
| |


| 0,001 | 
| |


| 0,001 | 
| |


| 0,001 | 
| |


| 0,003 | 
| |


| 0,004 | 
| |


| 0,005 | 
| |


| 0,005 | 
| |


| 0,008 | 
| |


| 0,008 | 
| |


| 0,01 | 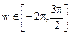
| |


| 0,01 | 
| |


| 0,03 | 
| |


| 0,03 | 
| |


| 0,03 | 
|
Задача 3.
Построить график функции R2(w) в полярных координатах, зависящий от функции R1(w) на указанном интервале (табл. 6). Номер варианта выбрать в соответствии с номером в списке журнала.
В математической системе MathCad создать файл и решить в нем поставленную задачу в соответствии с вариантом (таблица 6). Сохранить файл под именем «Полярные2-Фамилия» локально на диске.
ЛАБОРАТОРНАЯ РАБОТА №6.
Символьные вычисления.
Задача I.
Дана функция  :
:
а) Разложите по степеням функцию  с порядком разложения 5, 9, 15 членов;
с порядком разложения 5, 9, 15 членов;
б) Определите функцию f1(x) которая будет включать 5 членов разложения, функцию f2(x), которая будет включать 9 членов разложения и функцию f3(x), которая будет включать 15 членов разложения;
в) Посчитайте производную от функции f1(x);
г) Постройте на одном графике функцию  и ее представления в виде функций f1(x), f2(x) и f3(x);
и ее представления в виде функций f1(x), f2(x) и f3(x);
д) С помощью расчетов с плавающей точкой преобразуйте дробные коэффициенты при неизвестных в функциях f1(x), f2(x) и f3(x) в вещественные числа с 8-ю значащими цифрами.
ВЫПОЛНЕНИЕ:
I.а. Из математического анализа известно, что любую функцию  , заданную на интервале [a,b] (на данном интервале функция должна существовать) можно разложить в ряд Тейлора. При этом полученное разложение на данном интервале [a,b] будет отличаться от функции
, заданную на интервале [a,b] (на данном интервале функция должна существовать) можно разложить в ряд Тейлора. При этом полученное разложение на данном интервале [a,b] будет отличаться от функции  на
на  (
( – бесконечно малая величина).
– бесконечно малая величина).
|
|
|
Для того чтобы функцию  разложить в ряд Тейлора необходимо:
разложить в ряд Тейлора необходимо:
– определите в системе MathCad саму функцию в виде:  ;
;
– выделите переменную, относительно которой необходимо произвести разложение в ряд (рис. 35);

Рис. 35.
– выполните последовательность действий: меню Символы-Переменная-Разложить;
– в появившемся диалоговом окне «Разложить» укажите количество членов разложения (порядок разложения). По условию необходимо указать 5 (рис. 2) и активизировать кнопку Ок.

Рис. 36.
– далее ниже функции будет отображен рядв виде  .
.
– аналогично самостоятельно получите разложение с 9-ю и с 15-ю членами разложения (рис. 37).
|
|
|

Рис. 37.
I.б. Для определения функции  создайте запись в системе MathCad
создайте запись в системе MathCad  и скопируйте после знака присвоить ряд Тейлора с 5-ю членами разложения без величины
и скопируйте после знака присвоить ряд Тейлора с 5-ю членами разложения без величины  (рис. 38).
(рис. 38).

Рис. 38.
Аналогично определите функции  – с 9-ю членами разложения и
– с 9-ю членами разложения и  – с 15-ю членами разложения.
– с 15-ю членами разложения.
I.в. Для того, чтобы посчитать производную от функции  установите курсор в том месте, где хотите определить производную и на наборной панели «Матанализ» активизируйте кнопку нахождения первой производной
установите курсор в том месте, где хотите определить производную и на наборной панели «Матанализ» активизируйте кнопку нахождения первой производной  . Создайте запись
. Создайте запись  и активизируйте кнопку Enter.
и активизируйте кнопку Enter.
I.г. Для построения графика в декартовой системе координат установите курсор в том месте рабочего листа, где будет располагаться левый верхний угол будущего графика и активзируйте кнопку «Декартов график»  с наборной панели «Графики».
с наборной панели «Графики».
В местозаполнитель по оси ОХ внесите переменную х, по оси OY через запятую внесите три функции  .
.
I.д. Для того, чтобы выполнить арифметические операции в выражении с результатом в форме числа с плавающей точкой необходимо:
– выделить все выражение, дробные коэффициенты которого необходимо преобразовать в вещественные числа с плавающей запятой (рис. 39);

Рис. 39.
– выполните последовательность действий меню Символы-Расчеты-С плавающей запятой;
|
|
|
– в появившемся диалоговом окне (рис. 40) укажите количество знаков после запятой (по условию 8) и активизируйте кнопку Ок.

Рис. 40.
– после этого ниже выделенного выражения система MathCad выдаст новое выражение, в котором все дробные коэффициенты будут преобразованы в числа с плавающей запятой (рис. 39). При этом общее количество цифр в каждом числе будет равно 8;
– аналогично преобразуйте дробные коэффициенты в вещественные с плавающей точкой в ряде Тейлора с 9-ю членами и с 15-ю членами.
Задача IІ.
Дана функция  :
:
a) Разложите функцию y(x) в ряд Тейлора до 10 членов. Обозначьте полученное разложение функцией y1(x);
b) Постройте график функции y(x) и ее представления в виде функций y1(x).
c) На интервале, где функция y(x) совпадает со своим разложением, то есть с функцией y1(x) найдите значение площади функции y(x) и её разложения y1(x). Добейтесь, чтобы значение площадей функций y(x) и y1(x) совпадали до 3-его знака после запятой;
ВЫПОЛНЕНИЕ:
II.а. Для разложения функции  в ряд Тейлора:
в ряд Тейлора:
– создайте в системе MathCad запись  ;
;
– ниже создайте в системе MathCad запись  ;
;
– выделите переменную х, относительно которой необходимо произвести разложение в ряд;
– выполните последовательность действий: меню Символы-Переменная-Разложить;
– в появившемся диалоговом окне «Разложить» укажите количество членов разложения (порядок разложения). По условию необходимо указать 10 и активизируйте кнопку Ок.
– далее, ниже функции будет отображен полученный ряд;
– выделите полученный ряд (без последнего члена) и скопируйте в буфер обмена с помощью комбинаци клавиш Ctrl+C (или меню Правка-Копировать);
– ниже полученного ряда создайте запись  и после знака присвоить (:=) вставьте данные из буфера обмена. Получится запись (рис. 41).
и после знака присвоить (:=) вставьте данные из буфера обмена. Получится запись (рис. 41).

Рис. 41.
II.b. Для построения графика в декартовой системе координат:
– установите курсор в том месте рабочего листа, где будет располагаться левый верхний угол будущего графика и активзируйте кнопку «Декартов график»  с наборной панели «Графики».
с наборной панели «Графики».
– в местозаполнитель по оси ОХ внесите переменную х, по оси OY через запятую внесите две функции  . Получится график функции (рис. 42).
. Получится график функции (рис. 42).

Рис. 42.
– с помощью диалогового окна Трассировка (След) установите интервал [a,b], на котором функции  и
и 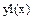 совпадают (рис. 42). Чтобы вызвать диалоговое окно Трассировка, вызовите контекстное меню графика (выполните щелчок правой кнопкой мыши на графике) и из контекстного меню вызовите команду Трассировка (След). Установите курсор в ту точку на графике, координаты которой хотите узнать и в диалоговом окне Трассировки (рис. 43) будет определена координата х и y интересующей Вас точки.
совпадают (рис. 42). Чтобы вызвать диалоговое окно Трассировка, вызовите контекстное меню графика (выполните щелчок правой кнопкой мыши на графике) и из контекстного меню вызовите команду Трассировка (След). Установите курсор в ту точку на графике, координаты которой хотите узнать и в диалоговом окне Трассировки (рис. 43) будет определена координата х и y интересующей Вас точки.
|
|
|

Рис. 43.
Точка а – левая граница интервала по оси ОХ, на котором функции  и
и 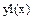 совпадают, точка b – правая граница интервала по оси ОХ, на котором функции
совпадают, точка b – правая граница интервала по оси ОХ, на котором функции  и
и 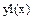 совпадают.
совпадают.
– определите переменные а и b. В данном случае в системе MathCad создадим запись а:=0, b:=0.7228.
II.с. Найдём площадь функции y(x) и её разложения y1(x) на интервале [a,b], имея в виду, что площадь – это определенный интеграл функции на интервале [a,b]. Для этого:
– установите курсор в том месте, где будете находить определенный интеграл;
– на наборной панели «Матанализ» активизируйте кнопку определенного интеграла  ;
;
– заполните пустые местозаполнители следующим образом  и активизируйте клавишу Enter. Справа будет указана площадь фигуры, ограниченной функцией y(x) сверху на интервале [a,b];
и активизируйте клавишу Enter. Справа будет указана площадь фигуры, ограниченной функцией y(x) сверху на интервале [a,b];
– аналогично найдите площадь функции y1(x) на интервале [a,b];
– изменяя значения границ интервала, то есть переменных а и b добейтесь, чтобы значения площадей функции y(x) и y1(x) отличались только в четвёртом знаке.
Задача III.
Дан полином  :
:
а) Вычислите коэффициенты полинома по степени х. Определите коэффициент при х0;
б) Вычислите коэффициенты полинома по степени y. Определите коэффициент при y0;
в) Вычислите коэффициенты полинома по степени z. Определите коэффициент при z0;
ВЫПОЛНЕНИЕ:
Операция Polynomial Coefficients (Коэффициенты полинома) служит для вычисления коэффициентов полинома. Операция применяется, если заданное выражение – полином (степенной многочлен) или может быть представлено таковым относительно выделенной переменной. Результатом операции является вектор с коэффициентами полинома. Операция полезна при решении задач полиномиальной аппроксимации и регрессии..
III.а. Введите полином в виде
 . Выделите переменную, относительно которой необходимо получить коэффициенты полинома. В данном случае выделите переменную х и выполните последовательность действий меню Символы-Коэффициенты полинома. Ниже система MathCad выдаст коэффициенты полинома при переменной х (рис. 44).
. Выделите переменную, относительно которой необходимо получить коэффициенты полинома. В данном случае выделите переменную х и выполните последовательность действий меню Символы-Коэффициенты полинома. Ниже система MathCad выдаст коэффициенты полинома при переменной х (рис. 44).
|
|
|
|
|
|
|
|
|
|

Рис. 44.
III.b. Выделите переменную, относительно которой необходимо получить коэффициенты полинома. В данном случае выделите переменную y и выполните последовательность действий меню Символы-Коэффициенты плинома. Ниже система MathCad выдаст коэффициенты полинома при переменной y (рис. 44).
III.c. Выделите переменную, относительно которой необходимо получить коэффициенты полинома. В данном случае выделите переменную z и выполните последовательность действий меню Символы-Коэффициенты плинома. Ниже система MathCad выдаст коэффициенты полинома при переменной z (рис. 44).
Задача IV.
Дано выражение  .
.
а) замените в выражении  переменную
переменную  на коэффициент х0 из предыдущего примера, полученного при разложении по степени x. Новое выражение обозначьте через
на коэффициент х0 из предыдущего примера, полученного при разложении по степени x. Новое выражение обозначьте через 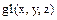 . Разверните полученное выражение, то есть откройте скобки и приведите подобные.
. Разверните полученное выражение, то есть откройте скобки и приведите подобные.
б) замените в выражении  переменную y на коэффициент y0 из предыдущего примера, полученного при разложении по степени y. Новое выражение обозначьте через
переменную y на коэффициент y0 из предыдущего примера, полученного при разложении по степени y. Новое выражение обозначьте через  . Разверните полученное выражение, то есть откройте скобки и приведите подобные.
. Разверните полученное выражение, то есть откройте скобки и приведите подобные.
в) замените в выражении  переменную z на коэффициент z0 из предыдущего примера, полученного при разложении по степени z. Новое выражение обозначьте через
переменную z на коэффициент z0 из предыдущего примера, полученного при разложении по степени z. Новое выражение обозначьте через  . Разверните полученное выражение, то есть откройте скобки и приведите подобные.
. Разверните полученное выражение, то есть откройте скобки и приведите подобные.
ВЫПОЛНЕНИЕ:
Операция Substitute (Замена) возвращает новое выражение, полученное путем подстановки на место указанной переменной некоторого другого выражения. Последнее должно быть подготовлено и скопировано (операциями Cut или Copy) в буфер обмена. Наряду с получением результата в символьном виде эта команда позволяет найти и числовые значения функции некоторой переменной путем замены ее на числовое значение.
IV.а. Для того, чтобы заменить в выражении  переменную
переменную  на коэффициент х0 из предыдущего примера:
на коэффициент х0 из предыдущего примера:
– внесите выражение, определяющее коэффициент при х0 из пункта 3.а. В данном случае в системе MathCad необходимо создать запись  , выделить её и с помощью комбинации клавиш Ctrl+C (или меню Правка-Копировать) скопируйте её в буфер обмена;
, выделить её и с помощью комбинации клавиш Ctrl+C (или меню Правка-Копировать) скопируйте её в буфер обмена;
– ниже внесите сам полином в виде  ;
;
– с учетом того, что в буфере находится выражение, определяющее коэффициент при переменной х0, выделите в полиноме переменную х и выполните последовательность действий меню Символы-Переменная-Замена;
– ниже будет выдан полином в котором переменная х заменена на выражение при х0 из пункта 3.а.
Чтобы открыть скобки в полученном выражении и привести подобные выполните последовательность действий:
– выделите выражение, в котором необходимо привести подобные и открыть скобки;
– выполните меню Символы-Развернуть;
– ниже система MathCad выдаст развернутый вариант выделенного выражения.
IV.б. Аналогичные действия проделайте для коэффициентов при y0 и z0.
Задача V.
Разложите на элементарные дроби выражение  .
.
ВЫПОЛНЕНИЕ:
Операция Convert to Partial Fraction (Преобразование в частичные доли) возвращает символьное разложение выражения, представленное относительно заданной переменной в виде суммы правильных целых дробей.
Для того, чтобы выполнить разложение дробно-рациональной функции на элементарные дроби выполните:
– введите само выражение, подлежащее разложению на элементарные дроби;
– выделите переменную, относительно которой необходимо разложить дробь, в данном случае выделите переменную х;
– выполните последовательность действий меню Символы-Переменная-Преобразование в частичные доли;
– ниже система MathCad выдаст разложение выражения, представленное относительно заданной переменной х в виде суммы правильных целых дробей.
Задача VI.
Разложите на множители выражение  ;
;
ВЫПОЛНЕНИЕ:
Операция Factor Expression (Разложить на множители (Фактор)) используется для факторизации – разложения выражений или чисел на простые множители. Она способствует выявлению математической сущности выражений; к примеру, наглядно выявляет представление полинома через его действительные корни, а в том случае, когда разложение части полинома содержит комплексно-сопряженные корни, порождающее их выражение представляется квадратичным трехчленом. Примеры действия этой операции даны на рис. 45. В большинстве случаев (но не всегда) операция факторизации ведет к упрощению выражений.

Рис. 45. Примеры действия команды Factor Expression.
Для того, чтобы выполнить разложение функции на множители выполните:
– введите само выражение, подлежащее разложению на множители. В данном случае введите  ;
;
– выделите все выражение, которое необходимо разложить на множители;
– выполните последовательность действий меню Символы-Фактор;
– ниже система MathCad выдаст разложение выделенного выражения на множители.
Задача VII.
Решите уравнение  с подстановкой коэффициентов a, b, c.
с подстановкой коэффициентов a, b, c.
ВЫПОЛНЕНИЕ:
– создайте новый файл в системе MathCad;
– выведите на экран наборную панель «Символы»  ;
;
– введите выражение  ;
;
– установите курсор в конец выражения  ;
;
– на наборной панели «Символы» активизируйте команду substitute;
– внесите данные согласно условию а = 2  ;
;
– в положении, когда курсор установлен после цифры 2, активизируйте команду substitute на наборной панели «Символы» и внесите b = 3;
– в положении, когда курсор установлен после цифры 3, активизируйте команду substitute на наборной панели «Символы» и внесите с = -4;
– в положении, когда курсор установлен после цифры 3, активизируйте команду solve на наборной панели «Символы» и в пустой местозаполнитель внесите х (рис. 46);

Рис. 46.
– активизируйте клавишу Enter на клавиатуре.
ВЫПОЛНИТЬ САМОСТОЯТЕЛЬНО
Задача 1.
Дана функция  . Функцию выбрать из таблицы 7 в соответствии с номером в списке журнала.
. Функцию выбрать из таблицы 7 в соответствии с номером в списке журнала.
Т а б л и ц а 7.
Варианты заданий
1) 
| 8) 
|
2) 
| 9) 
|
3) 
| 10) 
|
4) 
| 11) 
|
5) 
| 12) 
|
6) 
| 13) 
|
7) 
| 14) 
|
15) 
|
а) Разложите по степеням функцию  с порядком разложения 5, 9, 15 членов;
с порядком разложения 5, 9, 15 членов;
б) Определите функцию f1(x) которая будет включать 5 членов разложения, функцию f2(x), которая будет включать 9 членов разложения и функцию f3(x), которая будет включать 15 членов разложения;
в) Посчитайте производную от функции f1(x);
г) Постройте на одном графике функцию  и ее представления в виде функций f1(x), f2(x) и f3(x);
и ее представления в виде функций f1(x), f2(x) и f3(x);
д) С помощью расчетов с плавающей точкой преобразуйте дробные коэффициенты при неизвестных в функциях f1(x), f2(x) и f3(x) в вещественные числа с точностью после запятой до 8-ого знака.
Задача 2.
Дана функция y(x). Функцию выбрать из таблицы 8 в соответствии с номером в списке журнала.
Т а б л и ц а 8.
Варианты заданий
1) 
| 8) 
|
2) 
| 9) 
|
3) 
| 10) 
|
4) 
| 11) 
|
5) 
| 12) 
|
6) 
| 13) 
|
7) 
| 14) 
|
15) 
|
а) Разложите функцию y(x) в ряд Тейлора до 10 членов. Обозначьте полученное разложение функцией y1(x);
б) На интервале, где функция y(x) совпадает со своим разложением, то есть с функцией y1(x) найдите значение площади функции y(x) и её разложения y1(x). Добейтесь, чтобы значение площадей функций y(x) и y1(x) совпадали до 3-его знака после запятой;
в) Постройте график функции y(x) и ее представления в виде функций y1(x).
Задача 3.
Дан полином. Полином выбрать из таблицы 9 в соответствии с номером в списке журнала.
Т а б л и ц а 9.
Варианты заданий
1) 
|
2) 
|
3) 
|
4) 
|
5) 
|
6) 
|
7) 
|
8) 
|
9) 
|
10) 
|
11) 
|
12) 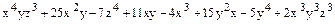
|
13) 
|
14) 
|
15) 
|
а) Вычислите коэффициенты полинома по степени х. Определите коэффициент при х0;
б) Вычислите коэффициенты полинома по степени y. Определите коэффициент при y0;
в) Вычислите коэффициенты полинома по степени z. Определите коэффициент при z0;
Задача 4.
Дано выражение  . Выражение выбрать из таблицы 10 в соответствии с номером в списке журнала.
. Выражение выбрать из таблицы 10 в соответствии с номером в списке журнала.
Т а б л и ц а 10.
Варианты заданий
1) 
| ||||
2) 
| ||||
3) 
| ||||
4) 
| ||||
5) 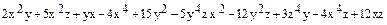
| ||||
6) 
| ||||
7) 
| ||||
Воспользуйтесь поиском по сайту:  ©2015 - 2026 megalektsii.ru Все авторские права принадлежат авторам лекционных материалов. Обратная связь с нами...
|

