 |
Исследование функций с помощью математического пакета MathCad.
|
|
|
|
Исследовать функцию  и построить её график, а также график всех её ассимптот (если таковые имеются).
и построить её график, а также график всех её ассимптот (если таковые имеются).
1) Найти первую производную данной функции;
2) Найти критические точки функции;
3) Найти вторую производную данной функции;
4) Найти точки перегиба;
5) Найти область определения данной функции;
6) Определить поведение функции в граничных точках области определения;
7) Найти все ассимптоты функции.
8) Построить график функции и графики всех найденных ассимптот.
ВЫПОЛНЕНИЕ:
1) Запишите функцию в виде:  . С помощью меню Вид - Панели инструментов - Вычисления вызовите на экран панель инструментов, предназначенную для нахождения производных и интегралов, рис. 18.
. С помощью меню Вид - Панели инструментов - Вычисления вызовите на экран панель инструментов, предназначенную для нахождения производных и интегралов, рис. 18.
 |
|

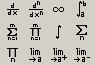
Рис. 18.
Установите курсор в то место, где вы будете находить первую производную и активизируйте кнопку (Первая производная), рис. 18.
Создайте запись: 
Установите курсор в конец введенной формулы рис. 19.

Рис. 19.
Вызовите на экран панель инструментов (Выражения) рис. 20.

|

Рис. 20.
На данной панели инстрементов активизируйте кнопку (Оценка). Нажмите кнопку Enter. Первая производная будет иметь вид рис. 21:

|

Рис. 21.
2) Для нахождения критических точек необходимо найти значения переменной x, при которых первая производная будет равняться 0. Для этого скопируйте выражение полученной первой производной ниже всех записей и с помощью панели инструментов (Булевы операторы) приравняйте первую производную к 0. Получите следующую запись, рис. 22:

Рис. 22.
Далее курсором выделите ту переменную, относительно которой необходимо разрешить уравнение. В данном случае этой переменной будет являться переменная x рис. 23.
|
|
|
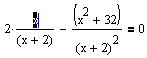
Рис. 23.
Выполните последовательность действий меню Символы – Переменные – Вычислить. После выполнения данной последовательности действий на экране, ниже записи первой производной, будут вычилены корни первой производной. Корни первой производной являются критическими точками исследуемой функции.
3) Для нахождения второй производной на панели иструментов Вычисления активизируйте кнопку (Производная n- ого порядка) рис. 18. Создайте запись рис. 24:

Рис. 24.
Нажмите Enter.
Вторая производная будет иметь вид рис. 25:
|


Рис. 25.
4) Для нахождения точек перегиба необходимо найти значения переменной x, при которых вторая производная будет равняться 0. Выполнить самостоятельно аналогично пункту 2.
5) Область определения для данной функции  . (В MathCad никуда не записывать).
. (В MathCad никуда не записывать).
6) Граничными точками области определения для данной функции являются точки:  . Чтобы определить поведение функции в граничных точках области определения функции необходимо найти пределы функции во всех граничных точках области опреления. Для этого установите курсор в ту область, где хотите найти предел и активизируйте на панели инструментов Вычисления кнопку (Двусторонний предел) рис. 26.
. Чтобы определить поведение функции в граничных точках области определения функции необходимо найти пределы функции во всех граничных точках области опреления. Для этого установите курсор в ту область, где хотите найти предел и активизируйте на панели инструментов Вычисления кнопку (Двусторонний предел) рис. 26.
|

|



|
Рис. 26.
Создайте запись рис. 27:

Рис. 27.
Нажмите Enter.
Предел в граничной точке области определения будет найден, рис. 28:

Рис. 28.
Аналогично найдите пределы во всех граничных точках области определения, с учетом того, что в точках разрыва (для данной функции точкой разрыва является x=-2) необходимо находить левосторонний и правосторонние пределы (рис. 26).
7) Для нахождения ассимптоты необходимо построить следующую функцию:  , где
, где  ,
,  . Для нахождения переменных k и b создайте в MathCad следующие записи рис. 29:
. Для нахождения переменных k и b создайте в MathCad следующие записи рис. 29:
|
|
|


Рис. 29.
Следовательно, функция ассимптоты будет иметь вид:  – уравнение ассимптоты. Задайте в MathCad уравнение ассимптоты. Если какой-то из пределов на рис. 29 не существует, значит данная функция
– уравнение ассимптоты. Задайте в MathCad уравнение ассимптоты. Если какой-то из пределов на рис. 29 не существует, значит данная функция  ассимптот не имеет.
ассимптот не имеет.
8) Для построение графиков функций  и ассимптоты
и ассимптоты  (если она есть) установите курсор в ту область, где вы хотите построить графики и активизируйте кнопку (Декартовы координаты) на панели инструментов (Графики) рис. 30.
(если она есть) установите курсор в ту область, где вы хотите построить графики и активизируйте кнопку (Декартовы координаты) на панели инструментов (Графики) рис. 30.
 |

Рис. 30.
Заполните пустые слоты графика следующим образом, рис. 31:

Рис. 31.
ВЫПОЛНИТЬ САМОСТОЯТЕЛЬНО
Постановка задачи: в соответствии с номером в списке журнала исследовать функцию f(x) (табл. 4) и построить её график, а также график всех её ассимптот (если таковые имеются).
1) Найти первую производную данной функции;
2) Найти критические точки функции;
3) Найти вторую производную данной функции;
4) Найти точки перегиба;
5) Найти область определения данной функции;
6) Определить поведение функции в граничных точках области определения;
7) Найти все ассимптоты функции.
8) Построить график функции и графики всех найденных ассимптот.
В математической системе MathCad создать файл и решить в нем поставленную задачу в соответствии с вариантом (таблица 4). Вариант выбирается по номеру в списке журнала. Сохранить файл под именем «Исследование-Фамилия» локально на диске.
Т а б л и ц а 4.
Варианты заданий
| № варианта | Функция f(x) | № варианта | Функция f(x) | ||
а)  б)
б) 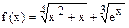
| а) 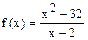 б)
б) 
| ||||
а)  б)
б) 
| а)  б)
б) 
| ||||
а)  б)
б) 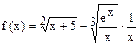
| а)  б)
б) 
| ||||
а)  б)
б) 
| а)  б)
б) 
| ||||
а)  б)
б) 
| а)  б)
б) 
| ||||
а)  б)
б) 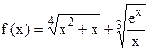
| а)  б)
б) 
| ||||
а)  б)
б) 
| а)  б)
б) 
| ||||
а)  ; б) ; б) 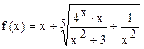 . .
| |||||
ЛАБОРАТОРНАЯ РАБОТА №5.
|
|
|


