 |
Контрольная работа №2. Тема 4. Транспортная задача. Тема 5. Игровые модели. Тема 6. Сетевое планирование. Методические указания по выполнению контрольных работ
|
|
|
|
КОНТРОЛЬНАЯ РАБОТА №2
Тема 4. Транспортная задача
Задача 4. Три склада обслуживают пять магазинов одним товаром. Первый склад располагает a1, второй a2, третий a3 единицами товара. Каждому из пяти магазинов требуется по плану b1, b2, b3, b4, b5 единиц товара. Известны тарифы всех перевозок, заданные матрицей тарифов С.
1) Установить, является ли данная транспортная задача закрытой.
2) Составить план перевозок по методу минимального тарифа и проверить является ли он опорным.
2) Найти общую стоимость перевозок для этого плана.
3) Проверить является ли составленный план оптимальным, пользуясь методом потенциалов.
4) Составить математическую модель для данной транспортной задачи.
Варианты заданий:
№ 31. a1 =120, a2 =80, a3 =100;
b1 = 85, b2 = 65, b3 =50, b4 =70, b5 =30.
С = 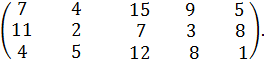
№ 32. a1 =200, a2 =140, a3 =150;
b1 = 90, b2 = 50, b3 =120, b4 =100, b5 =130.
С = 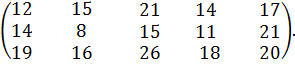
№ 33. a1 =150, a2 =200, a3 =60;
b1 = 80, b2 = 70, b3 =90, b4 =70, b5 =100.
С = 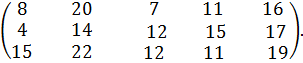
№ 34. a1 =180, a2 =280, a3 =220;
b1 =170, b2 = 120, b3 =190, b4 =70, b5 =130.
С = 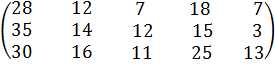 .
.
№ 35. a1 =140, a2 =300, a3 =240;
b1 =160, b2 = 130, b3 =180, b4 =80, b5 =130.
С = 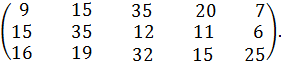
№ 36. a1 =160, a2 =270, a3 =250;
b1 =140, b2 = 120, b3 =200, b4 =70, b5 =150.
С = 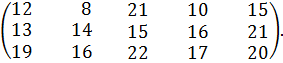
№ 37. a1 =200, a2 =250, a3 =300;
b1 =100, b2 = 170, b3 =190, b4 =110, b5 =180.
|
|
|
С = 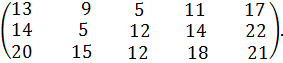
№ 38. a1 =150, a2 =250, a3 =200;
b1 =135, b2 = 115, b3 =140, b4 =120, b5 =90.
С = 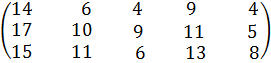 .
.
№ 39. a1 =250, a2 =200, a3 =150;
b1 =110, b2 = 120, b3 =130, b4 =100, b5 =140.
С = 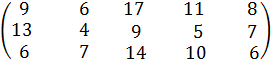 .
.
№ 40. a1 =350, a2 =400, a3 =250;
b1 =185, b2 = 265, b3 =290, b4 =170, b5 =90.
С =  .
.
Тема 5. Игровые модели
Задача 5. Игра задана платёжной матрицей А размера 2 x 2.
1) Найти верхнюю и нижнюю цену игры. Сделать выводы.
2) Записать смешанные стратегии игроков.
3) Составить математические модели задач для обоих игроков.
4) Найти оптимальные стратегии игроков и цену игры.
Варианты заданий:
№ 41. А = 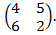 № 42. А =
№ 42. А = 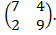 № 43. А =
№ 43. А = 
№ 44. А = 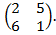 № 45. А =
№ 45. А =  № 46. А =
№ 46. А = 
№ 47. А = 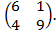 № 48. А =
№ 48. А =  № 49. А =
№ 49. А = 
№50. А = 
Тема 6. Сетевое планирование
Задача 6. Для планирования строительства торгового павильона фирмы составлен сетевой график, на котором отражены взаимосвязь, очерёдность и длительность выполнения всех работ с учётом их технологической последовательности. Построенный сетевой график имеет вид:
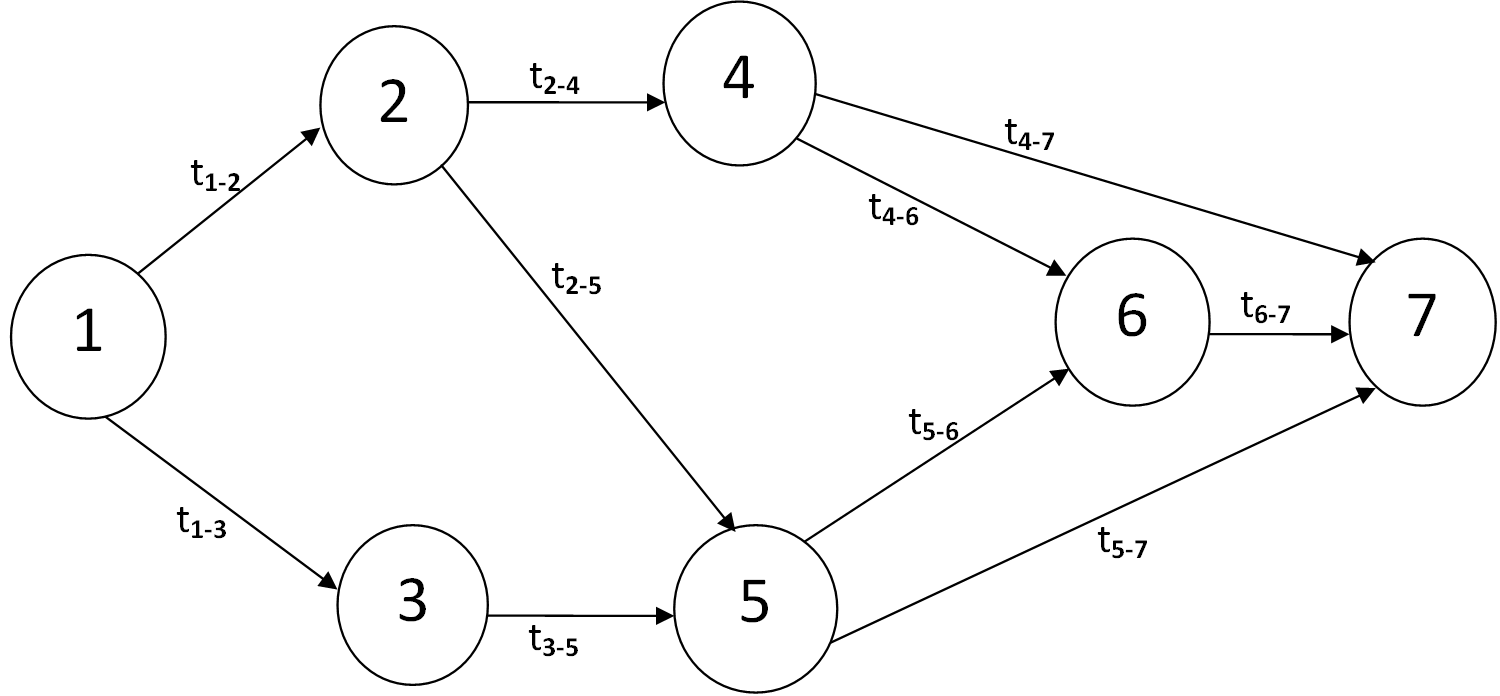
1) Выписать все полные пути, найти их длительности и указать критический путь.
2) Найти ранние и поздние сроки наступления событий и определить
резервы времени этих событий.
3) Рассчитать все виды резервов времени для каждой работы.
Варианты заданий:
№ 51. t 1-2 = 3; t 1-3 = 2; t 2-4 = 2; t 2-5 = 3; t 3-5 = 2;
t 4-6 = 7; t 4-7 = 5; t 5-6 = 3; t 5-7 = 2; t 6-7 = 6.
№ 52. t 1-2 = 2; t 1-3 = 6; t 2-4 = 4; t 2-5 = 7; t 3-5 = 5;
t 4-6 = 3; t 4-7 = 2; t 5-6 = 2; t 5-7 = 8; t 6-7 = 4.
|
|
|
№5 3. t 1-2 = 5; t 1-3 = 8; t 2-4 = 3; t 2-5 = 4; t 3-5 = 3;
t 4-6 = 2; t 4-7 = 4; t 5-6 = 7; t 5-7 = 1; t 6-7 = 3.
№ 54. t 1-2 = 4; t 1-3 = 2; t 2-4 = 5; t 2-5 = 6; t 3-5 = 4;
t 4-6 = 3; t 4-7 = 3; t 5-6 = 5; t 5-7 = 6; t 6-7 = 5.
№ 55. t 1-2 = 6; t 1-3 = 5; t 2-4 = 3; t 2-5 = 2; t 3-5 = 6;
t 4-6 = 5; t 4-7 = 4; t 5-6 = 8; t 5-7 = 2; t 6-7 = 9.
№ 56. t 1-2 =10; t 1-3 = 3; t 2-4 = 6; t 2-5 = 5; t 3-5 = 8;
t 4-6 = 9; t 4-7 =14; t 5-6 =10; t 5-7 = 5; t 6-7 = 4.
№ 57. t 1-2 = 7; t 1-3 = 4; t 2-4 = 9; t 2-5 = 6; t 3-5 = 7;
t 4-6 = 4; t 4-7 =12; t 5-6 = 5; t 5-7 = 6; t 6-7 = 8.
№ 58. t 1-2 = 8; t 1-3 = 5; t 2-4 = 7; t 2-5 = 10; t 3-5 =12;
t 4-6 = 5; t 4-7 = 9; t 5-6 = 4; t 5-7 =13; t 6-7 = 2.
№ 59. t 1-2 = 9; t 1-3 = 6; t 2-4 = 8; t 2-5 = 5; t 3-5 = 9;
t 4-6 = 3; t 4-7 = 6; t 5-6 = 9; t 5-7 =14; t 6-7 = 7.
№60. t 1-2 = 3 t 1-3 = 2; t 2-4 = 4; t 2-5 =11; t 3-5 =12;
t 4-6 = 7; t 4-7 = 8; t 5-6 = 6; t 5-7 =14; t 6-7 = 5.
МЕТОДИЧЕСКИЕ УКАЗАНИЯ ПО ВЫПОЛНЕНИЮ КОНТРОЛЬНЫХ РАБОТ
КОНТРОЛЬНАЯ РАБОТА №1
Тема 1. Прогнозирование
Прогнозирование – это вероятностное суждение о перспективах развития экономических показателей в будущем.
В логистике прогнозируются спрос, объёмы продаж, расход материальных ресурсов, уровень запасов и др. От точности и достоверности прогноза этих показателей зависит эффективность логистического менеджемента. Чаще всего прогноз названных показателей связывают исключительно со временем, предполагая, что через время учитывается влияние всех остальных факторов, таких как среднедушевой денежный доход, розничная цена, численность населения и проч.
Прогноз осуществляется на основе анализа тенденций развития. Под тенденцией понимают общее направление развития, которое называют «тренд ». Тренд характеризует основную закономерность изменения показателя во времени и определяется влиянием постоянно действующих факторов. Отклонения от тренда объясняются наличием случайных факторов. Выявленный тренд является моделью для прогнозирования.
При прогнозировании чаще других используются методы экстраполяции, т. е. распространения прошлых закономерностей на будущее. В этом случае исходная информация имеет вид динамического (временного) ряда. Динамический ряд – это упорядоченная совокупность значений показателя y за n предшествующих последовательных периодов времени t: yt = (y1, y2, …, y n ). По этим данным выполняется прогноз при условии, что процесс развития в будущем не претерпит существенных изменений, то есть будет эволюционным.
|
|
|
Данные динамического ряда образуют так называемую базовую линию, поскольку прогноз базируется на этих данных. Длина базовой линии n – количество наблюдаемых значений показателя у. Глубина прогноза m – это количество прогнозируемых значений. Глубина прогноза m должна быть значительно меньше длины базовой линии n.
Для выявления тренда часто используют так называемые регрессионные модели прогноза, которые представляет собой уравнения вида:
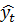 = f(t) + ɛ t ,
= f(t) + ɛ t ,
где f(t)–функция, описывающая тренд, ɛ t – случайная составляющая.
Наиболее простой и употребляемой моделью является уравнение линейной регрессии, когда в качестве тренда используется линейная функция f(t)= a*t + b. На графике линейная функция изображается в виде прямой линии, которая называется «прямая регрессии».
Параметры прямой регрессии a и b выбираются так, чтобы уравнение линейной регрессии наилучшим образом было приближено к базовым данным уt. Обычно наилучшее приближение определяется по методу наименьших квадратов (МНК): должна быть наименьшей сумма квадратов отклонений базовых значений уt от соответствующих значений f(t), посчитанных по уравнению регрессии.
В соответствии с этим требованием для вычисления параметров a и b
линейной регрессии получены формулы:
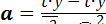 ;
; 
После нахождения уравнения линейной регрессии:
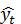 ≈ а*t + b,
≈ а*t + b,
оценивают его адекватность, то есть насколько хорошо оно аппроксимирует (описывает) базовые данные. Для этого применяют различные способы. Один из них основан на нахождении средней ошибки аппроксимации. Если эта ошибка невелика, то полученное линейное уравнение регрессии используют для прогнозирования.
|
|
|
Однако найденное уравнение тренда характеризует лишь средний уровень динамики ряда. Возникает необходимость оценить ошибку прогноза при определённом уровне доверия, задаваемом вероятностью р. Обычно эти вероятности берут высокими: 90%, 95% или 99%. В результате указывают доверительный интервал для прогноза с данной надёжностью р.
Задача 1–10. Известны данные об уровне продаж некоторого товара уt в тыс. руб. за десять месяцев текущего года.
1) Изобразить эти данные графически.
2) Построить линейную регрессионную модель для прогнозирования.
3)Оценить адекватность модели с помощью средней ошибки аппроксимации.
4) Сделать прогноз продаж на два последующих месяца.
5) Найти ошибку прогноза при уровне надежности р = 90%.
6) Указать относительную точность прогноза и доверительный интервал прогноза для каждого из прогнозных месяцев.
уt = (65; 66; 69; 72; 73; 71; 76; 78; 77; 78).
|
|
|


