Решение. Контрольная работа №2. Тема 4. Транспортная задача

Решение

    1) Оптимальный размер заказа х*   находим по формуле:

 ,

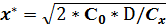где  С_х – годовая стоимость хранения одной единицы товара, которая по условию составляет 15% её  закупочной цены С = 60руб/ед.  Следовательно С_х = 0, 15_* С = 0, 15_*60 = 9руб/год, и тогда

х* = 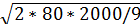= 188, 56 ед.

   2) Минимальные годовые издержки на завоз и хранение одной партии товара составят:

y_min =С_0*D/x* + С_х*x*/2 = 80*2000 /188, 56 + 9*188, 56 /2 =

                   = 848, 5363 + 848, 5363 ≈ 1697, 07 руб.

   3) Количество поставок в год: N = D / х* = 2000/188, 56 = 10, 6 ≈ 11 раз в год.

   4) Интервал времени между двумя последовательными поставками  с учётом того, что по условию задачи Т = 1год = 300 дней, составит:

τ = T/N = 300/ 10, 6 ≈ 28 рабочих дней.

   5) Уровень повторного заказа Q_з – это количество единиц товара при достижении которого нужно делать повторный заказ. Пусть известно время τ _зп, необходимое для завоза одной партии товара. Очевидно, что за 1день завозимое количество товара составит ( D / T ) ед., и тогда за время   τ _зп дней будет доставлено ( D / T )_* τ _зп. ед. товара, это и есть уровень повторного заказа. По условию задачи  τ _зп = 5дней. Тогда

Q_з = ( D / Т )_* τ _зп = (2000/300)_*5 ≈ 33, 33 ед.

Это означает, что когда уровень запаса снизится до 33, 33 ед. нужно сделать повторный заказ на 188, 56 ед., и тогда новая партия товара будет доставлена к моменту полного расходования предыдущей партии.

   6) Можно получить скидку 7% у поставщика, если размер заказа будет не

менее 200 единиц. Выясним, стоит ли воспользоваться скидкой.

   При использовании скидок снижаются расходы на закупку товара, но повышаются затраты на его хранение. Поэтому необходимо сделать расчёты.

    Общие  годовые издержки  с учётом затрат на покупку товара  в объёме D ед. по цене С  руб. /ед. составят:

y = С _* D + С_{0 *} D / x + С_{х *} x /2,

    Чтобы выяснить, выгодна ли скидка, сначала вычислим общие годовые издержки   у  без учёта скидки, беря найденный оптимальный размер заказа   х*= 188, 56 ед., заданные цены на товар С = 60 руб/ед.  и  годовые нормы его хранения   С_х = 9руб/ед.

y = 60*2000 +80*2000/188, 56 + 9*188, 56/2 ≈  121697 руб.

     Теперь найдём издержки с учётом скидки. Для этого берём   х = 200 – это наименьший уровень заказа по сниженным ценам. Новая цена на товар после снижения её на 7% составит С_нов. = (1– 0, 07) * С = 0, 93*60 = 55, 8 руб/ед. Так как нормы хранения товара заданы в процентах от цены, то они также изменятся и будут равны: С_{х нов.} = 0, 15* С_нов. = 0, 15*55, 8 = 8, 37 руб/ед. в год. Тогда общие годовые издержки составят:

y = 55, 8*2000 +80*2000/200 + 8, 37*200/2 ≈  113237руб.

    Выбирают тот вариант, где издержки меньше. Для решаемой задачи 113237 руб. ˂ 121697 руб., следовательно, воспользоваться скидкой выгодно.

    В этом случае будем поставлять по 200 ед. товара, тогда количество поставок в год составит N = D / x = 2000/200 = 10 раз,  а интервал времени между поставками будет τ = Т / N = 300/10 = 30 рабочих дней. Уровень заказа останется тем же Q_з ≈  33, 33 ед.

 

КОНТРОЛЬНАЯ РАБОТА №2

Тема 4. Транспортная задача

     Пусть необходимо перевезти некоторый однородный груз от нескольких поставщиков нескольким потребителям.  

    Поставщики:  А₁,   А₂,  …  , А_m

    Их запасы:       а₁,    а₂,  …   , а_m.  

    Потребители:        В₁,   В₂, …, В_n

     Их потребности:  b₁,    b₂,  …    , b_n.

    Известны тарифы перевозок c _ij – это стоимость перевозки 1 единицы груза от каждого поставщика Аi   каждому потребителю Вj:  i = 1, 2, …, m;                   j= 1, 2,  …     , n.

    Обозначим поставки   x _ij–  это количество груза, перевозимое от поставщика Аi потребителю Вj. Очевидно, что соблюдается условие не отрицательности:   x_ij  ≥ 0.

     Общая стоимость всех перевозок Z = c_11* x ₁₁ + c_12* x ₁₂ + … + c_mn* x _mn.         Нужно найти план перевозок { x _ij}, который обеспечит минимальные общие затраты на перевозки:  Z " min.

     Пусть суммарные запасы поставщиковравны суммарным потребностям  потребителей∑ а _i = ∑ b _j. В этом случае транспортная задача называется закрытой. Транспортная задача называется открытой, если нарушено условие баланса между суммарными запасами груза и суммарными потребностями, то есть ∑ а _i ≠ ∑ b _j. Открытую транспортную задачу всегда легко привести к закрытой задаче путём введения фиктивного поставщика или фиктивного потребителя с недостающим количеством груза и  нулевыми тарифами.

     В случае, когда транспортная задача закрытая весь груз от поставщиков будет вывезен и все потребители удовлетворены.

     Данные задачи и её решение удобно располагать в таблице перевозок.

 

Задача 31–40. Три склада обслуживают пять магазинов одинаковым товаром. Первый склад располагает a1, второй a2, третий a3 единицами товара. Каждому из пяти магазинов требуется по плану соответственно b1, b2, b3, b4, b5 единиц товара. Известны тарифы всех перевозок, заданные матрицей тарифов С.  

    1) Установить, является ли данная транспортная задача закрытой.

    2) Составить план перевозок по методу минимального тарифа и проверить является ли он опорным.

    2) Найти общую стоимость перевозок для этого плана.

    3) Проверить является ли составленный план оптимальным, пользуясь методом потенциалов.

    4) Составить математическую модель для данной транспортной задачи.

                     a1 =110, a2 =190,   a3 =160;     

                           b1 =120, b2 = 100, b3 =80, b4 =70, b5 =90.

                         С =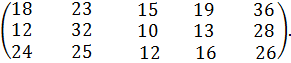

⇐ Предыдущая123456Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: