 |
Тема 5. Игровые модели. Решение
|
|
|
|
Тема 5. Игровые модели
Теория игр – это раздел математики, где моделируются конфликтные ситуации с учётом их неопределённости и рассматриваются методы решения полученных моделей.
Игра – это упрощённая математическая модель конфликтной ситуации.
Неопределённость ситуации часто возникает из-за отсутствия информации о действиях других игроков. Такие игры называются стратегическими.
Если количество участников игры два, то игра называется парной.
Если выигрыш одного из игроков равен проигрышу другого, то игра называются « с нулевой суммой ».
Часто игра задаётся платёжной матрицей. Такие игры называются матричными. Каждый элемент платёжной матрицы равен выигрышу первого игрока и проигрышу второго. Если элемент матрицы отрицательный, то проигрывает первый игрок, а второй выигрывает.
В дальнейшем будем рассматривать стратегические парные матричные игры с нулевой суммой. Такие игры наиболее часто встречаются в экономической практике и их теория хорошо разработана.
Методы и рекомендации теории игр применимы к многократно повторяющимся конфликтным ситуациям между игроками, например такими как, поставщик - потребитель, продавец-покупатель, банк - клиент.
Пусть игра задана платёжной матрицей размера 2 × 2. Это означает, что первый игрок А имеет две чистые стратегии А1 и А2, которым соответствуют строки матрицы. Второй игрок В имеет также две чистые стратегии В1 и В2, которым соответствуют столбцы платёжной матрицы. Игрок А стремится выиграть как можно больше, а игрок В – проиграть как можно меньше. При этом оба не рискуют.
Оптимальной называется стратегия, которая при многократном повторении ходов обеспечивает игроку А максимально возможный средний выигрыш, а игроку В наименьший средний проигрыш. При этом максимальный средний выигрыш игрока А совпадает с наименьшим средним проигрышем игрока В и называется ценой игры.
|
|
|
Задача 41- 50. Игра задана платёжной матрицей А размера 2 x 2.
1) Найти верхнюю и нижнюю цену игры. Сделать выводы.
2) Записать смешанные стратегии игроков.
3) Составить математические модели задач для обоих игроков.
4) Найти оптимальные стратегии игроков и цену игры.
А = 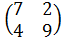
Решение
Элементы заданной платёжной матрицы А означают, что если первый игрок выберет стратегию А1, а второй игрок применит стратегию В1, то первый игрок А выиграет а11 = 7 ед., а второй игрок В проиграет эти 7 ед. Аналогично, если первый игрок выберет стратегию А1, а второй игрок выберет стратегию В2, то первый игрок А выиграет а12 = 2 ед., а второй игрок В проиграет 2 ед. Далее, если первый игрок выберет стратегию А2, а второй игрок выберет стратегию В1, то первый игрок А выиграет а21 = 4 ед., а второй игрок В проиграет 4 ед. И, наконец, если первый игрок выберет стратегию А2, а второй игрок выберет стратегию В2, то первый игрок А выиграет а 22 = 9 ед., а второй игрок В проиграет эти 9 ед.
1) Пусть первый игрок А выбрал стратегию А1. Тогда он получит выигрыши либо 7, либо 2, в зависимости от того, какую стратегию выберет игрок В. Наименьший из выигрышей α 1= min( 7; 2) = 2 называется гарантированным (обязательным) выигрышем игрока А при выборе им стратегии А1. Аналогично при выборе игроком А стратегии А2 его гарантированный выигрыш составит α 2= min( 4; 9) = 4. Из гарантированных выигрышей игрока А выберем наибольший: α = max(α 1; α 2) = max(2; 4) = 4. Этот наибольший из гарантированных выигрышей игрока А называется нижней ценой игры: α = max(min aij). Поведение игрока А, основанное на максимизации минимальных выигрышей, называется принципом максимина ( maxmin ).
|
|
|
Пусть второй игрок В выбрал стратегию В1. Тогда его проигрыши составят либо 7, либо 4, в зависимости от того, какую стратегию выберет игрок А. Наибольший из проигрышей β 1 = max( 7; 4) = 7 является наихудшим проигрышем игрока В при выборе им стратегии В1. Аналогично при выборе игроком В стратегии В2 его наихудший проигрыш составит β 2= max(2; 9) = 9. Из наихудших проигрышей игрока В выберем самый маленький проигрыш: α = min(β 1; β 2) = min(7; 9) = 7. Этот наименьший из наибольших проигрышей игрока В называется верхней ценой игры: β = min(max aij). Поведение игрока В, основанное на минимизации максимальных проигрышей, называется принципом минимакса ( minmax ).
Итак, нижняя цена игры α = 4, верхняя цена игры β = 7. Всегда α ≤ β.
Так как α ≠ β, то игра не решается в чистых стратегиях. То есть, нет такой чистой пары стратегий, применяя которые можно достичь наилучшего результата одновременно для обоих игроков.
2) Для любой матричной игры нижняя цена игры не превосходит верхней цены игры, то есть α ≤ β. Если α = β, то игра решается в чистых стратегиях, при этом цена игры υ = α = β. Это означает, что первый игрок А выиграет не менее υ, а второй проиграет не более υ ед.
Если α ˂ β, то решение игры в чистых стратегиях невозможно. В этом случае игру решают в смешанных стратегиях. Смешанная стратегия означает, что игрок А использует обе свои чистые стратегии, причём первую свою чистую стратегию А1 с вероятностью р1, а вторую чистую стратегию А2 с вероятностью р2. Очевидно, что при этом р1 ≥ 0, р2 ≥ 0 и р1 + р2 = 1.
Аналогично, второй игрок В также использует обе свои чистые стратегии, причём первую чистую стратегию В1 с вероятностью ԛ 1, а вторую чистую стратегию В2 с вероятностью ԛ 2. Очевидно, что при этом ԛ 1 ≥ 0, ԛ 2 ≥ 0 и ԛ 1 + ԛ 2 = 1. Таким образом, смешанные стратегии игроков задаются в виде векторов вероятностей р и ԛ .
Смешанная стратегия игрока А: р =( р1; р2 ), р1 ≥ 0, р2 ≥ 0 и р1+р2 = 1.
Смешанная стратегия игрока В: ԛ =( ԛ 1; ԛ 2 ), ԛ 1 ≥ 0, ԛ 2 ≥ 0 и ԛ 1+ԛ 2 = 1.
|
|
|
Любая матричная игра имеет оптимальное решение в смешанных стратегиях. Цена игры υ означает выигрыш игрока А, равный проигрышу игрока В и заключена между нижней и верхней ценой игры: α ˂ υ ˂ β.
3) Запишем данную задачу в виде:
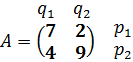
Используя эту запись легко понять, что если второй игрок В применит свою чистую стратегию В1, то игрок А выиграет 7 ед. с вероятностью р1 и 4 ед. с вероятность р2, тогда ожидаемый средний выигрыш игрока А составит: (7*р1 + 4*р2), при этом он должен быть равен цене игры υ. Аналогично, если второй игрок В применит свою чистую стратегию В2, то средний ожидаемый выигрыш игрока А составит: 2*р1 + 9*р2, при этом он также равен цене игры υ.
Если первый игрок А применит свою чистую стратегию А1, то ожидаемый средний проигрыш игрока В будет: 7*ԛ 1 + 2*ԛ 2, при этом он равен цене игры υ. Аналогично, если первый игрок А использует свою чистую стратегию А2, то средний ожидаемый проигрыш игрока В составит: 4*ԛ 1+ 9*ԛ 2, и он также должен быть равен цене игры υ.
В результате математические модели задач для обоих игроков будут записаны в виде систем уравнений:
Игрок А
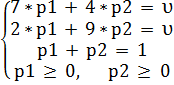
| Игрок В
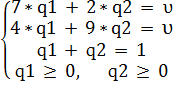
|
4) Для нахождения оптимальных стратегий игроков решим обе полученные модели, как системы трёх уравнений с тремя неизвестными: р1, р2, υ и q1, q2, υ. Для этого в обеих системах вычтем из первого уравнения второе, чтобы исключить неизвестное υ и, выразив из полученного соотношения одну вероятность через другую, подставим найденное выражение в третье уравнение.
5*р1 – 5*р2 = 0 3*q1 – 7*q2 = 0
5*p1= 5*p2 3*q1 = 7*q2
p1 = p2 q1 = (7/3)*q2
p2 +p2 = 1 (7/3)*q2 + q2 = 1
2*p2 = 1 (10/3)*q2 = 1
|
|
|
p2 = 1/2; p1 = 1/2; q2 = 3/10; q1 = 7/10;
υ = 7*р1 + 4*р2 = υ =7*q1 + 2*q2 =
=7*0, 5+4*0, 5 =5, 5. = 7*0, 7 + 2*0, 3 =5, 5.
Цена игры в обеих задачах должна быть одна и та же. У нас υ = 5, 5, отметим, что она заключена между нижней и верхней ценой игры: α = 4 ˂ 5, 5 ˂ 7 = β.
Ответ: р = (0, 5; 0, 5), ԛ = (0, 7; 0, 3), υ = 5, 5.
Этот результат означает, что если при многократном повторении игры первый игрок будет применять свои чистые стратегии с вероятностями 50%, то он получит выигрыш не менее 5, 5. Если при этом второй игрок, независимо от поведения первого, будет на 70% применять свою первую стратегию и на 30% вторую стратегию, то он проиграет не более 5, 5 ед.
Тема 6. Сетевое планирование и управление ( СПУ )
СПУ даёт методы планирования и управления большим комплексом связанных работ. Оно основано на моделировании процессов деятельности с помощью сетевых графиков.
Сетевой график – это наглядное изображение плана работ с чётким определением всех взаимосвязей между работами. Основные элементы сетевого графика: работы и события.
Работа – это процесс протяжённый во времени, связанный с каким-либо видом деятельности или ожиданием. Например, доставка товара, обучение персонала. Изображается в виде направленной дуги (или отрезка) с указанием времени выполнения работы. Длительность дуг указывается числом, масштаб длительности при этом не соблюдается.
Событие – это момент завершения работы, после которого можно начинать выполнения следующей работы. Событие не имеет протяжённости во времени. Например, товар доставлен, персонал обучен, документы поступили. События изображаются кружками, с указанием их порядкового номера.
На сетевом графике события (кружки) связаны работами (дугами). Например, работа i-j, здесь i – номер предшествующего события, j – номер последующего события, tij – длительность работы, в часах, днях, неделях, месяцах.
Каждая дуга имеет направление, указанное стрелкой. Дуга направлена от предшествующего события i кпоследующему событию j. Таким образом, каждое событие может иметь как входящие, так и выходящие дуги.
При построении сетевого графика соблюдаются следующие правила.
– Только одно событие не имеет входящих дуг, оно называется начальным, его номер 1.
– Только одно событие не имеет выходящих дуг, оно называется конечным.
– Остальные события должны иметь как входящие, так и выходящие дуги, по одной или по несколько.
|
|
|
– Каждая работа имеет предшествующее и завершающее событие, то есть, нет дуг, которые ниоткуда не выходят или никуда не входят.
– Два события могут быть связаны только одной дугой, или совсем не связаны.
– Не должно быть изолированных частей, не связанных с остальным графиком.
– Не должно быть замкнутых циклов.
– Если события не связаны работой, но между ними есть логическая связь, то вводится фиктивная работа, изображаемая пунктирной дугой, соединяющей эти события, её длительность равна нулю.
– Если имеются параллельные работы, связывающие одни и те же события, то вводится промежуточное событие и фиктивная работа.
Задача 51-60. Для планирования строительства торгового павильона фирмы составлен сетевой график, на котором отражены взаимосвязь, очерёдность и длительность в днях выполнения всех работ с учётом их технологической последовательности. Построенный сетевой график имеет вид:
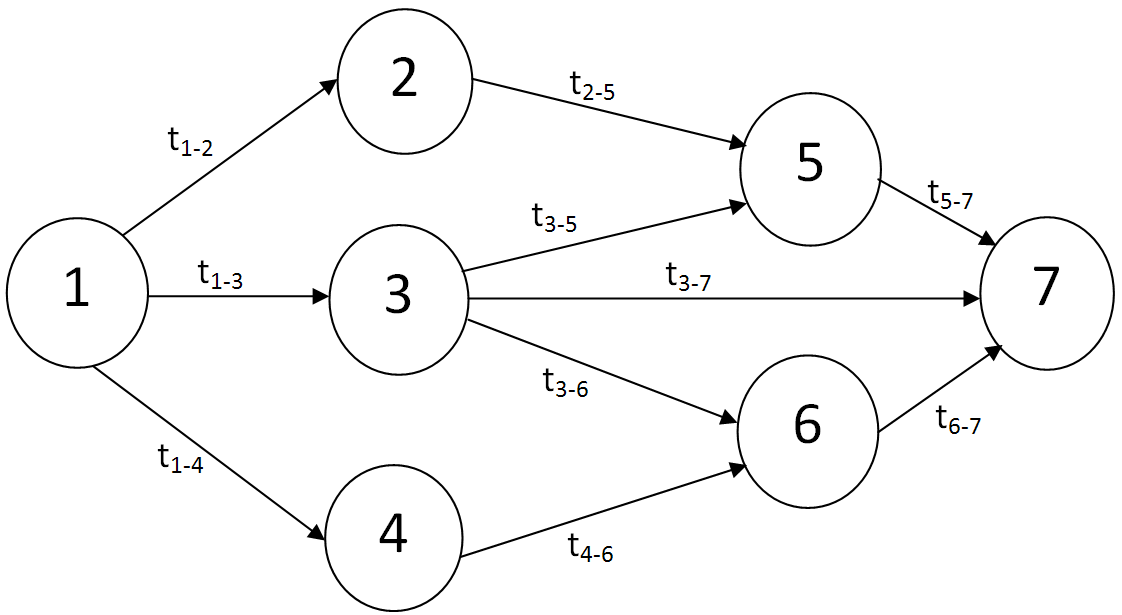
1) Выписать все полные пути, найти их длительности и указать критический путь.
2) Найти ранние и поздние сроки наступления всех событий и определить их резервы времени.
3) Рассчитать все виды резервов времени для каждой работы.
t 1-2 = 2; t 1-3 = 4; t 1-4 = 3; t 2-5 = 4; t 3-5 = 7;
t 3-6 = 8; t 3-7 = 6; t 4-6 = 6; t 5-7 = 2; t 6-7 = 5.
Решение
1) Проставим на сетевом графике около каждой дуги, изображающей работу, заданную длительность этой работы.
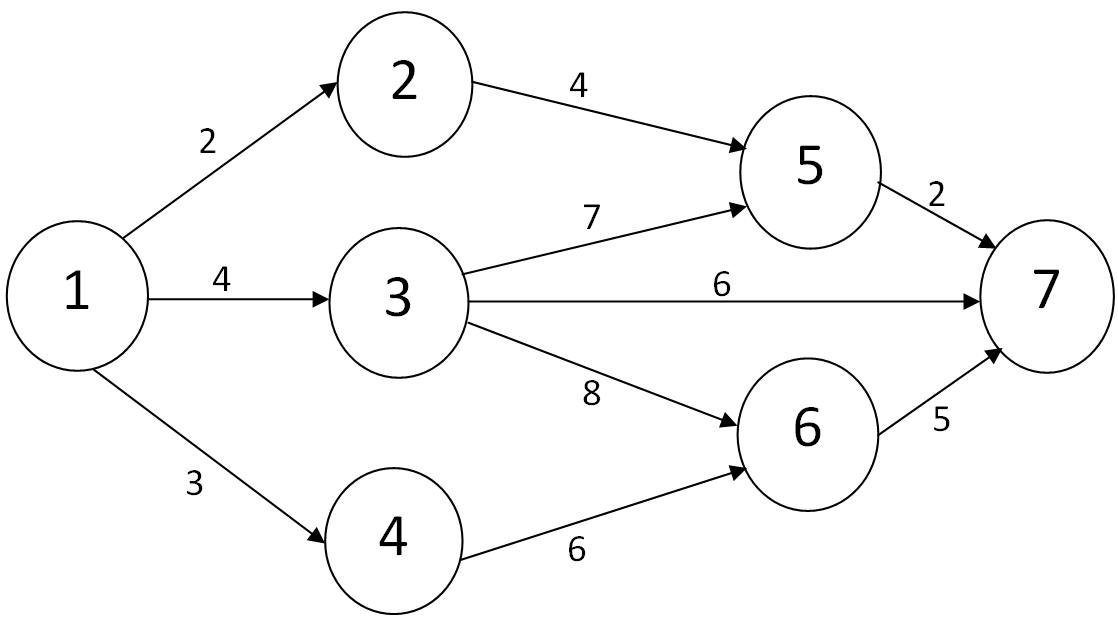
Путь – это упорядоченная последовательность дуг, когда конец предыдущей дуги совпадает с началом следующей, например 3 – 6 – 7.
Длина пути – это суммарная длительность всех включённых в него дуг.
Полный путь – это путь от начального события до конечного события. Полных путей обычно бывает несколько.
Критический путь – это самый длинный из всех полных путей. Его длина равна минимальному времени, за которое успевают завершиться все работы сетевого графика. Может оказаться, что критических путей несколько, но при этом их длительности совпадают. На сетевом графике критические пути выделяют жирной линией.
Выпишем все полные пути для данной задачи и найдём их длительности в днях:
Полные пути Их длительности
1 – 2 – 5 – 7 2 + 4 + 2 = 8
1 – 3 – 5 – 7 4 + 7 + 2 = 13
1 – 3 – 7 4 + 6 = 10
1 – 3 – 6 – 7 4 + 8 + 5 = 17
1 – 4 – 6 – 7 3 + 6 + 5 = 14
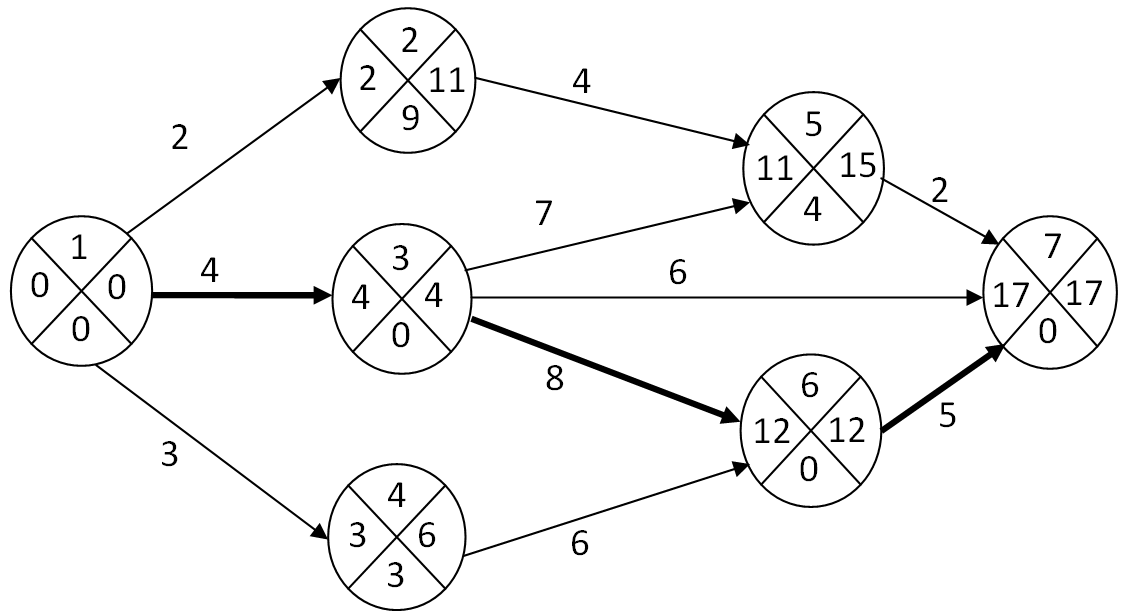
Видим, что самая большая длительность 17 дней. Это время, необходимое для выполнения всего комплекса работ, так как за это время успевают завершиться все работы. Соответствующий этому времени полный путь 1 – 3 – 6 – 7, является критическим. Выделим его на сетевом графике жирной линией.
Работы, лежащие на критическом пути, называются критическими работами. Эти работы самые напряжённые. Увеличение длительности выполнения любой из критических работ ведёт к увеличению срока выполнения всего комплекса работ, то есть всего проекта.
2) Найдём ранние и поздние сроки наступления событий.
Ранний срок наступления события Tp(j) – это минимальное время, необходимое для наступления события j, при условии, что наступят все предшествующие события i:
Tp(j) = max(Tp(i) + ti-j),
где i номера всех событий непосредственно предшествующих событию j. Максимум берётся потому, чтобы успели завершиться все предшествующие работы, изображённые входящими дугами.
Ранние сроки вычисляются по входящим дугам. Вычисления начинаются от начального события, ранний срок наступления которого считается нулевым, и заканчиваются конечным событием.
Tp(1) = 0;
Tp(2) = Tp(1) + t1-2 = 0 +2 = 2;
Tp(3) = Tp(1) + t1-3 = 0 +4 = 4;
Tp(4) = Tp(1) + t1-4 = 0 +3 = 3;
Tp(5) = max (Tp(2) + t2-5; Tp(3) + t3-5) = max (2 +4; 4 +7) = max (6; 11) = 11.
Tp(6) = max (Tp(3) + t3-6; Tp(4) + t4-6) = max (4 +8; 3 +6) = max (12; 9) = 12.
Tp(7) = max (Tp(3) + t3-7; Tp(5) + t5-7; Tp(6) + t6-7) = max (4 +6; 11 +2; 12+5) =
= max (11; 13; 17) = 17.
Ранний срок наступления конечного события всегда равен длине критического пути.
Поздний срок наступления события Tп(i) – это максимально возможный срок наступления этого событияi, не нарушающий сроков наступления всех последующих событий, а следовательно и сроков выполнения всего проекта:
Tп(i) = min(Tп(j) – ti-j ),
где jномера всех событий, непосредственноследующих за событием i.
Поздние сроки вычисляются по выходящим дугам, начиная от конечногособытия, поздний срок которого совпадает с начальным сроком его наступления.
Tп(7) = Tр(7) = 17;
Tп(6) = Tп(7) – t6-7 = 17 – 5 = 12;
Tп(5) = Tп(7) – t5-7 = 17 – 2 = 15;
Tп(4) = Tп(6) – t4-6 = 12 – 6 = 6;
Tп(3) = min (Tп(5) – t3-5; Tп(6) – t3-6; Tп(7) – t3-7) =
= min (15 – 7; 12 – 8; 17 – 6) = min (8; 4; 11) = 4;
Tп(2) = Tп(5) – t2-5 =15 – 4 = 11;
Tп(1) = min (Tп(2) – t1-2; Tп(3) – t1-3; Tп(4) – t1-4) =
= min (11 – 2; 4 – 4; 6 – 3) = min (9; 0; 3) = 0.
Поздний срок наступления начального события всегда равен нулю, как и его ранний срок.
Резервы времени событий R(i) – показывают, на какой предельный срок времени можно сдвигать наступление события i, чтобы не нарушились сроки наступления всех остальных событий:
R(i) = Tп(i) –Tp(i).
R(1) = Tп(1) –Tp(1) = 0 – 0 = 0; R(5) = Tп(5) – Tp(5) = 15 – 11 = 4;
R(2) = Tп(2) –Tp(2) = 11 – 2 = 9; R(6) = Tп(6) – Tp(6) = 12 – 12 = 0;
R(3) = Tп(3) –Tp(3) = 4 – 4 = 0; R(7) = Tп(7) – Tp(7) = 17 – 17 = 0.
R(4) = Tп(4) – Tp(4) = 6 – 3 = 3;
События, лежащие на критическом пути, не имеют резервов времени, то есть для них R = 0. Таким образом, критический путь проходит через события 1; 3; 6; 7 с нулевыми резервами времени.
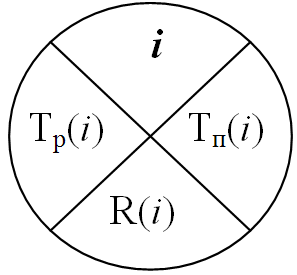
Все полученные результаты в процессе расчётов наносят на сетевой график в кружках для каждого события i, где i = 1, 2, …, 7, в следующем порядке:
3) Рассчитаем все виды резервов времени для каждой из работ.
Критические работы не имеют резервов времени, их нельзя сдвигать, не нарушив длительности выполнения всего проекта. Остальные, работы можно сдвигать на определённые сроки, оставаясь в рамках длительности проекта. Таким образом, эти некритические работы имеют резервы времени. Различают четыре вида резервов времени работ: полный, гарантийный, свободный и независимый.
1) Пр – полный резерв: Пр = Tп(j) –Tp(i) – ti-j, это максимально возможный резерв времени у исполнителя работы i-j.
2) Гр – гарантийный резерв: Гр = Tп(j) – Tп(i) – ti-j гарантирует время выполнения работы i-j по поздним срокам.
3) Ср – свободный резерв: Ср = Tр(j) – Tp(i) – ti-j этот резерв можно использовать одновременно для всех работ.
4) Нр – независимый резерв: Нр = Tр(j) – Tп(i) – ti-j резерв времени у исполнителя работы i-j, который он имеет независимо от исполнителей остальных работ.
Резервы времени работ удобно рассчитывать в таблице.
В первой колонке таблицы перечисляются все данные работы, в рассматриваемой задаче их 10. Во второй колонке – длительности этих работ, которые даны по условию. В третьей и четвёртой колонках вписаны ранний и поздний сроки наступления предшествующего события i для каждой работы. Эти сроки были посчитаны в предыдущем пункте и проставлены в кружках для каждого события (слева). В пятой и шестой колонках помещены ранний и поздний сроки наступления последующего события j для каждой работы. Их также удобно выписать из сетевого графика, где они помещены в кружках (справа).
Остальные четыре колонки заполнены резервами времени работ. Их удобно заполнять по столбцам. Полный резерв Пр вычисляют как разность позднего срока последующего события j и раннего срока предыдущего события i за вычетом длительности работы ti-j. Аналогично заполняется столбец для Гр –гарантийного резерва, по разности поздних сроков последующего и предшествующего событий каждой работы за вычетом длительности работы. Столбец для Ср –свободного резерва заполняется аналогично предыдущему, но с использованием ранних сроков. И, наконец, последний столбец для независимого резерва Нрвычисляют как разность, стоящих в расчётной таблице рядом, раннего срока последующего события j и позднего срока предыдущего события i, за вычетом длительности работы ti-j. Если при вычислении независимого резерва получают отрицательный результат, то берут Нр = 0. Например, для работы 2 – 5:
Нр = Tp(5) – Tп(2) – t2-5 = 11 – 11 – 4 = – 4 ˂ 0, поэтому берём Нр = 0.
| Работы i – j | Длит. ti-j | Предшеств. i | Послед. j | Резервы времени работ | |||||
| Tp(i) | Tп(i) | Tp(j) | Tп(j) | Пр | Гр | Ср | Нр | ||
| 1 – 2 | |||||||||
| 1 – 3 | |||||||||
| 1 – 4 | |||||||||
| 2 – 5 | |||||||||
| 3 – 5 | |||||||||
| 3 – 6 | |||||||||
| 3 – 7 | |||||||||
| 4 – 6 | |||||||||
| 5 – 7 | |||||||||
| 6 – 7 | |||||||||
Всегдасправедливо соотношение: Нр ≤ Гр ≤ Пр;
Нр ≤ Ср ≤ Пр.
Критические работы резервов времени не имеют. Результаты, полученные в таблице, этому требованию удовлетворяют. Действительно, для критических работ 1-3, 3-6, 6-7 все резервы времени нулевые.
***
|
|
|


