Равновесие жидкости в поле силы тяжести. Поверхность уровня.

В случае равновесия жидкости в поле земного тяготения на жидкость действует только сила тяжести, т.е.

X=Y=0, Z=-g.

Тогда основное дифференциальное уравнение статики (2.6) запишется в виде

. (2.7)

После интегрирования будем иметь

.

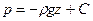Для определения постоянной интегрирования C рассмотрим резервуар, наполненный жидкостью, (Рис.2.4), со свободной поверхностью. Для точки лежащей на поверхности z=z_o, р=р_o. Подставив эти значения в уравнение (2.8), получим

C=р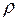_o+ gz_o.

Тогда уравнение (2.8) запишется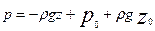

или - (2.9)

основное уравнение гидростатики; по нему можно подсчитать давление в любой точке покоящейся жидкости.

Или

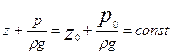. (2.9а)

 

Принимая во внимание, что разность z-z_o=h, а 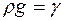- удельный вес, уравнение (2.9) можно переписать в виде

, (2.10)

где h- глубина погружения точки М.

Величины z и в гидростатике называют соответственно геометрической и пьезометрической высотой.

Сумма называется гидростатическим напором. Из уравнения (2.9а) видно, что гидростатический напор есть величина постоянная для всего объема неподвижной жидкости.

Согласно уравнению (2.10) давление в любой точке покоящейся жидкости складывается из двух величин: давления р₀ на внешней поверхности жидкости и давления, обусловленного весом вышележащих слоев жидкости.

Величина р₀ является одинаковой для всех точек объема жидкости, поэтому, учитывая свойство гидростатического давления, можно сказать, что давление, приложенное к внешней поверхности жидкости передается всем точкам этой жидкости и по всем направлениям одинаково – закон Паскаля.

Давление жидкости, как видно из формулы (2.10), возрастает с увеличением глубины по линейному закону и на данной глубине есть величина постоянная (см. рис 2.5).

 

Поверхность, во всех точках которой давление одинаково, называется поверхностью уровня.

- (2.11).

уравнение поверхности уровня.

Относительное равновесие. Движение резервуара с жидкостью по вертикали с постоянным ускорением.

Если же сосуд с жидкостью находится в неравномерном или непрямолинейном движении, то на частицы жидкости кроме силы тяжести действуют еще силы инерции, причем если они постоянны по времени, то жидкость принимает новое положение равновесия. Такое равновесие жидкости называется относительным покоем (равновесием).

При рассмотрении относительного равновесия обычно решаются две задачи: определяется форма поверхности уровня (равного давления) и выясняется характер распределения давления. Эти задачи решаются с помощью уравнени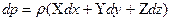й:

и

Движение резервуара с жидкостью по вертикали с постоянным ускорением а (рис.2.6).

Для определения формы поверхности равного давления воспользуемся уравнением (2.11). Проекции единичных массовых сил на координатные оси будут: . Знак «-»-равноускоренный подъем, «+»-спуск.

 

 

Рис.2.6. Вертикальное перемещение резервуара с жидкостью.

Составим уравнение поверхности уровня

(-g. 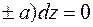. (2.12)

 

Если , то dz=0 и, следовательно, z=const, т.е.поверхности равного давления представляют собой горизонтальные плоскости. (При спуске и а=g 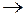невесомость).

Характер распределения давления в рассматриваемом случае получим из основного уравнения равновесия жидкости (2.6), которое принимает форму:

Интегрируя, получим

,

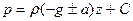где С – постоянная интегрирования, определяемая из граничных условий поверхности z=z₀, p=p₀.

После подстановки граничных условий, получаем закон распределения давления вдоль любой вертикали:

(2.13)

 

 

Относительное равновесие. Вращение цилиндрического сосуда с жидкостью с постоянной угловой скоростью.

⇐ Предыдущая12345678Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: