Уравнение неразрывности для несжимаемой и сжимаемой жидкости.

При рассмотрении движения сжимаемой жидкости будем предполагать, что движущая жидкость сплошь заполняет все пространство, т.е. пустоты или разрывы не образуются. Это условие называется условием неразрывности или сплошности движения.

в случае несжимаемой жидкости количество вытекшей жидкости вследствие условия неразрывности должно в точности равняться количеству втекшей жидкости. Если же за некоторый промежуток времени количество вытекшей жидкости будет превышать количество втекшей, то внутри этой поверхности произойдет изменение плотности. Сказанное выше можно представить в виде дифференциального уравнения, носящего название уравнения неразрывности или сплошности движения.

Рассмотрим фиксированную в пространстве замкнутую поверхность, имеющую форму прямоугольного параллелепипеда.

Пусть в единицу времени и через единицу площади левой грани параллелепипеда в направлении оси Х протекает масса жидкости u_x.

 

Так как u_x есть функция координат и времени, т.е. u_x=f(x, y, z, t),

надо найти f(x+ d_x, y, z, t). Но с точностью до малых первого порядка

f(x+ d_x, y, z, t)= f(x, y, z, t)+ ,

т.е. через единицу площади правой грани в единицу времени протекает в направлении оси Х масса жидкости, равная

.

Очевидно, разность между вытекшим и втекшим количеством жидкости будет

,

и, следовательно за время dt через грани площадью d_yd_z вытечет в направлении оси Х масса жидкости

.

Аналогично разности между вытекшим и втекшим количеством жидкости в направлении осей Y и Z.

Если эти выражения сложить, то получим суммарную разность между всей вытекшей и втекшей за время dt жидкостью:

Различие в количествах (массе) вытекшей и втекшей жидкости отразится на количестве жидкости внутри параллелепипеда. В самом деле, если в момент времени t плотность была , то в момент t+dt плотность будет равна

и, следовательно, за время dt количество (масса) жидкости внутри параллелепипеда изменится от величины до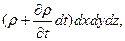

т.е. на величину

В силу условия неразрывности разность между количествами вытекшей и втекшей жидкости должна быть равна изменению количества жидкости внутри параллелепипеда. Поэтому получаем

или

(3.5)

Это уравнение носит название дифференциального уравнения неразрывности для сжимаемой жидкости.

Если движение сжимаемой жидкости установившееся, то, очевидно

и уравнение неразрывности примет вид

14. Уравнение Бернулли для элементарной струйки идеальной и реальной жидкости. Применим к массе жидкости в объеме участка струйки теорему механики об изменении кинетической энергии. Работа силы давления в первом сечении положительна,:

p₁dS_{1 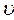1}dt.

Работа силы давления во втором сечении имеет знак минус и определяется выражением

- -p₂dS_{2 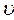2}dt.

Тогда работа сил давления будет

p_{1 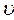1}dS₁dt-p_{2 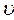2}dS₂dt.

Работа силы тяжести равна изменению потенциальной энергии положения участка струйки, поэтому надо из энергии положения жидкости в объеме 1 – 2 вычесть энергию положения жидкости в объеме . объемы, а следовательно, и силы тяжести заштрихованных элементов и равны между собой:

.

Тогда работа силы тяжести:

.

из кинетической энергии объема вычтем кинетическую энергию объема 1 – 2. Таким образом, приращение кинетической энергии равно

.

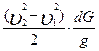Из всего этого, получается:

Разделив обе части уравнения на dG, и произведя сокращения, получим

(4.5)

где z – геометрическая высота, или геометрический напор;

- пьезометрическая высота, или пьезометрический напор;

- скоростная высота, или скоростной напор.

Уравнение (4.5) называется уравнением Бернулли для элементарной струйки идеальной несжимаемой жидкости.

 

при движении вязкой жидкости в уравнение Бернулли необходимо внести поправку на потери напора

 

15.Уравнение Бернулли для потока жидкости с поперечнымсечением конечных размеров.

При переходе от элементарной струйки идеальной жидкости к потоку реальной (вязкой) жидкости, имеющему конечные размеры, необходимо учесть неравномерность распределения скоростей по сечению, а также потери энергии (напора). Из–за неравномерного распределения скоростей по поперечному сечению приходится вводить в рассмотрение среднюю по сечению скорость .

 

Таким образом, уравнение Бернулли для потока конечного размера отличается от такового для элементарной струйки тем, что здесь скоростной напор, определяемый средней скоростью, дополнен коэффициентом ,, носящим название коэффициента Кориолиса.

представляет собой отношение действительной кинетической энергии потока в данном сечении к кинетической энергии того же потока и в том же сечении, но при равномерном распределении скоростей.

Величина этого коэффициента зависит от степени неравномерности распределения скорости по сечению. Этот коэффициент всегда > единицы (за исключением случая, когда местные скорости в данном сечении равны между собой, тогда =1) и при обычном распределении скоростей равняется 1,1;

 

⇐ Предыдущая12345678Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: