 |
Режимы течения в трубах. Число Рейнольдса.
|
|
|
|
Наблюдения показывают, что в природе существуют два различных вида (режима) течения жидкости:
1) слоистое упорядоченное, или ламинарное течение, при котором отдельные слои жидкости скользят относительно друг друга, не смешиваясь между собой;
2) неупорядоченное, или турбулентное, течение, когда частицы жидкости движутся по сложным, все время изменяющимся траекториям и в жидкости происходит интенсивное перемешивание.
опыт.
Переход от ламинарного течения к турбулентному происходит при определенной скорости (так называемой критической скорости), которая для труб разных диаметров оказывается различной, возрастающей с увеличением вязкости и снижающейся с увеличением диаметра трубы.
Оказалось, что режим потока жидкости в трубе зависит от безразмерного числа, которое учитывает основные факторы определяющие это движение: среднюю скорость 
, диаметр трубы d и вязкость жидкости 
. Это число называется числом Рейпольдса и имеет вид
.
Число Re, при котором происходит переход от ламинарного режима течения к турбулентному, называют критическим и обозначают Reкр (а соответствующую ему скорость называют критической скоростью)
Как показывают опыты для труб круглого сечения Reкр 
2300( 2000)
При Re<Reкр течение является ламинарным, при Re>Reкр – турбулентным. Точнее говоря, развитое турбулентное течение в трубах устанавливается
лишь при Re 4000, а при Re =2300 
4000 имеет место переходная критическая область.
Зная скорость движения жидкости, и ее вязкость и диаметр трубы, можно найти число Re и, сравнив его с Reкр, определить режим течения жидкости.
На практике имеют место как ламинарное, так и турбулентное течения, причем первое наблюдается в основном в тех случаях, когда по трубам движутся вязкие жидкости (смазочные масла), второе обычно там, где по тубам перетекают маловязкие жидкости (вода, бензин, спирт, газы).
|
|
|
Ламинарное течение в трубах
слоистое упорядоченное, или ламинарное течение, при котором отдельные слои жидкости скользят относительно друг друга, не смешиваясь между собой;
При движении жидкости по трубам основные изменения скорости и ускорения происходят вдоль оси трубопровода.
Изменение параметров вдоль двух других координат можно считать пренебрежимо малыми.
Средняя скорость равна 0,5 скорости максимальной.
закон сопротивления:
.
где 
- коэффициент потерь на трение для ламинарного течения:
.
Таким образом потеря напора на трение по длине при ламинарном течении пропорциональна скорости в первой степени, а коэффициент обратно пропорционален Re.
Коэффициент Кариолиса для ламинарного режима 
=2.
Турбулентное течение.
неупорядоченное, или турбулентное, течение, когда частицы жидкости движутся по сложным, все время изменяющимся траекториям и в жидкости происходит интенсивное перемешивание.
При турбулентном движении осредненная скорость мало меняется по сечению трубопровода. Область, где скорости почти не меняются по сечению, называется ядром течения, а слой у стенок, характеризующийся быстрым уменьшением значения скорости – пристенным слоем.
Экспериментально получена формула для определения распределения скорости по сечению
, (5.12)
где - скорость на расстоянии y от стенки;
- max скорость на оси трубопровода.
Показатель степени n зависит от числа Re для гидравлически гладких труб и от относительной шероховатости для труб вполне шероховатых.
при переходе к турбулентному течению заметны некоторый скачок сопротивления и затем более крутое нарастание величины 
. (рис. 5.7)
.
 |
Рис. 5.7. Зависимость от и Q.
|
|
|
Основной расчетной формулой для потерь напора при турбулентном течении в круглых трубах является известная уже формула Вейсбаха – Дарси,
имеющая вид
, где 
- коэффициент потерь на трение
где 
(к) – средняя высота бугорков шероховатости, d – диаметр трубы.
( или к)-шероховатость.
Когда шероховатость трубы не влияет на ее сопротивление (на ), трубу называют гидравлически гладкой. Для этих случаев коэффициент является функцией лишь числа Re: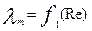 
Коэффициент трения определяется по формуле Б.Л. Шифринсона
.
|
|
|
