Главная | Обратная связь | Поможем написать вашу работу!

Последовательное соединение труб

Рассмотрим трубопровод, состоящий из труб разного диаметра (рис. 6.3), уложенных в одну линию одна вслед за другой (последовательное соединение труб). Уравнение Бернулли для этого случая запишется в виде:

где - потери напора на первом, втором и т.д. участках трубопровода.

Рис.6.3.Последовательное соединение трубопроводов

Потери напора на первом участке с диаметром трубы d₁:

Аналогично для последующих участков:

В последнем равенстве в скобках добавлено третье слагаемое – единица, учитывающая потери напора на выход (об этом говорилось ранее)

Таким образом, расчетное уравнение имеет вид:

. (6.5)

Из уравнения (6.5) видно, что решение первой и второй задач будет таким же, как для трубопровода постоянного диаметра.

Третья же задача, если в ней есть потребность определения всех диаметров для всех участков, становится неопределенной, т.к. в этом случае уравнение (6.5) содержало бы n неизвестных. Очевидно, что для определенности решения надо задавать диаметры труб для всех участков, кроме одного.

26. Расчет длинных трубопроводов в квадратичной областисопротивления.

Квадратичная область сопротивления – когда коэффициент гидравлического трения не зависит от числа Re, а определяется только относительной шероховатостью стенок трубопровода.

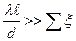
. (6.6)

Уравнение (6.3) приводится к виду

(6.7)

Уравнение (6.4) к виду

или , (6.8)

где А – удельное сопротивление трубопровода

. (6.9)

А полное сопротивление

S=A . (6.10)

Если обозначить

, (6.11)

то уравнение (6.7) примет вид

. (6.12)

Показатель К, имеющий размерность расхода, называется модулем расхода или расходной характеристикой трубопровода.

Показатели A, S,K представляют собой обобщенные гидравлические параметры трубопровода, использование которых значительно упрощает гидравлические расчеты.

27.

Параллельное соединение трубопроводов

Трубопровод в точке А разветвляется на несколько труб, которые затем вновь объединяются в точке В соединение трубопроводов.

Задача расчета состоит в том, чтобы определить расходы в отдельных ветвях системы Q₁, Q₂, …, Q_n, а также потери напора между точками А и В. Потери напора в любой трубе ответвления одинаковы, т.к. в обеих крайних точках разветвления имеется один и тот же напор Н₁ и конечный Н₂, т.е.

. (6.19)

Для первой ветви можно записать

(6.20)

Аналогично для других ветвей

(6.21)

;;.

Для решения данной системы дополним ее еще одним уравнением – уравнением расхода

Q=Q₁+Q₂+…+Q_n. (6.22)

Решение системы уравнений проводим следующим образом. Выражаем все расходы, начиная с Q₂, через Q₁

(6.23)

Откуда расход в первой ветви определится, как

. (6.24)

Зная величину Q₁, можно последовательно определить Q₂, Q₃,…, Q_n.

Величина потери напора определится как

. (6.25)

При расчете параллельных трубопроводов в неквадратичной области сопротивлений необходимо использовать поправочные коэф-ты .

(6.26)

- потеря напора (6.27)

28.. Непрерывная раздача расхода по пути

Рассмотрим случай непрерывной раздачи расхода на некотором участке трубопровода. При этом расход жидкости вдоль пути непрерывно уменьшается, т.е. движение жидкости происходит с переменным расходом

Решение задачи сводится к определению величины напора в трубопроводе постоянного диаметра.

Рис.6.5

Расход в начале участка раздачи

Q=Q_тр+Q_нр, (6.28)

где Q_тр – транзитный расход, расход оставшийся в трубопроводе ниже конца участка раздачи.

Определим потерянный напор на участке АВ. Потери напора dh_тр на элементарном участке трубопровода длиной dx, расположенном на расстоянии x от конца участка раздачи (сечение 1-1)

(6.29)

где Q – расход, проходящий в сечение 1-1:

. (6.30)

Подставляя выражение (6.30) в (6.29), получим

. (6.31)

проинтегрируем..

А=А_кв

(6.32)-эту не диктуй

При Q_тр=0, т.е. при отсутствии горизонтального расхода

. (6.33)

Для неквадратичной области сопротивления

(6.34)

где В - поправка к коэффициенту в связи с изменением средней скорости течения (для вполне шероховатых труб В 1; для гладких В 1,1)

29. Истечение жидкости из отверстий в тонкой стенке

Рис. 7.1. Истечение жидкости и отверстия в тонкой стенке.

Для определения скорости истечения жидкости запишем уравнение Бернулли для сечений 1-1 и 2-2, причем сечение 2-2 проведем через наиболее сжатый участок струй .

. (7.3)

Давление в сжатом сечении струи р можно принять равным атмосферному, т.е. р₀, т.к. истечение происходит в атмосферу.

Потери напора между сечениями 1-1 и 2-2 определяются формулой Вейсбаха

, (7.4)

где - коэффициент сопротивления отверстия.

Принимая . (на основании опытных данных), получим:

Решая это уравнение относительно , находим

. (7.5)

Разделив обе части равенства на , получим

Принимая во внимание, что , преобразуем записанную выше формулу к виду

(7.6)

имея в виду, что

(7.7)

и возведя обе части уравнения (7.6) в квадрат, получим:

откуда имеем

. (7.8)

Введем обозначение

(7.9)

где - коэффициент скорости истечения.

Тогда получаем (7.10)

При истечении из малых отверстий ()

. (7.11)

При малом влиянии вязкости =0; =1, вместо формулы (7.11) получаем

. (7.12)

Расход жидкости, выходящей из отверстия, находим по формуле

Подставляя вместо и их значения, имеем

Введем обозначение

(7.13)

где - коэффициент расхода отверстия.

Тогда получим формулу для определения расхода

. (7.14)

. (7.15)

30. Истечение жидкости из сосудов со свободной поверхностью

В случае истечения из сосудов со свободной поверхностью

(рис. 7.2) уравнение расхода (7.14) записывается в виде

(7.16)

где - высота уровня жидкости в сосуде над центром отверстия (при d<<H)

Рис. 7.2. Истечение Рис. 7.3. Истечение жидкости под

Жидкости из сосуда уровень(затопленное истечение).

со свободной поверхностью.

34. Гидравлический удар

Явление резкого повышения давления в трубопроводе при внезапном его перекрытии носит название «Гидравлического удара». Процесс этот очень быстротечен, и характеризуется чередованием резких повышений и понижений давления.