крА + крВ →LE (Ф=3 и С=0).

При этой температуре система остается до тех пор, пока не исчезнет одна из фаз. В данном случае полностью расплавятся кристаллы вещества А, а кристаллы вещества В — частично. Находящиеся в избытке по отношению к эвтектике, кристаллы В останутся в равновесии с жидким раствором.

Система снова становится двухфазной ( С=1 ) и ее температура повышается. Происходит дальнейшее плавление системы _крВ→ L . Кристаллы В , расплавляясь, изменяют состав жидкой фазы, согласно правой ветви ликвидус. Ее состав при определенной температуре легко найти с помощью конноды. Заканчивается плавление полным исчезновением кристаллов В при температуре Т₂ .

Кривая охлаждения сплава b аналогична кривой охлаждения сплава а, за исключением температуры начала кристаллизации и длины горизонтального участка.

Определение теплоты плавления компонента на основании диаграммы состояния с эвтектикой

Ветви ликвидуса диаграммы состояния с эвтектикой (рис. 4. 3а) характеризуют равновесие насыщенных расплавов с соответствующими кристаллами чистого вещества, т. е показывают растворимость соответствующего компонента в расплаве при данной температуре.

Растворимость твердых веществ в жидкости для идеальных систем выражается уравнением Шредера:

(4. 1)

где: 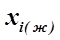 - мольная доля i -го компонента (растворителя) в жидком растворе;

 - теплота плавления чистого компонента i;

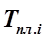 - температура плавления чистого компонента i;

T_L - температура начала кристаллизации раствора или температура, при которой насыщенный раствор и кристаллы чистого i -го компонента находятся в равновесии.

Данное уравнение справедливо для понижения температуры замерзания идеальных растворов, если в твердую фазу выделяется чистый растворитель, т. е. оно согласуется с данной диаграммой состояния.

Идеальными для рассматриваемой эвтектической системы можно принять растворы вблизи чистых компонентов, т. е. разбавленные.

Диаграмма состояния с эвтектикой позволяет по линии ликвидус определить состав насыщенного раствора ( 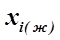) и температуру, при которой он находится в равновесии с кристаллами чистого растворителя ( T_L ), а также температуру плавления чистого растворителя ( Т_{пл. i} ). Подставляя эти данные в уравнение Шредера (4. 1), можно оценить теплоту плавления соответствующего растворителя .

Определение активности и коэффициента активности компонента на основании диаграммы состояния с эвтектикой

Расплавы данной системы в области средних концентраций не могут считаться идеальными и относятся к реальным. Для описания растворимости компонента в реальных растворах можно использовать понятие термодинамической активности компонентов и уравнение Шредера принимает вид:

(4. 2)

где: α _i, - активность i -го компонента в реальном насыщенном растворе с концентрацией х_i(ж), находящегося в равновесии с кристаллами чистого i -го компонента при температура T_L;

Т_{пл i} - температура плавления чистого компонента i.

Уравнение (4. 2) позволяет определить термодинамическую активность компонента, кристаллизующегося из раствора, если известна его теплота плавления 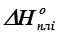. Значения T_{пл. i} и T_L для раствора с концентрацией х_i(ж} определяются по диаграмме состояния.

Зная активность компонента можно вычислить γ _i -коэффициент активности i -го компонента в реальном растворе из уравнения:

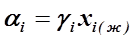
(4. 3)