 |
4.2.6. Диаграмма состояния с промежуточным химическим соединением, плавящимся инконгруэнтно
|
|
|
|
4. 2. 6. Диаграмма состояния с промежуточным химическим соединением, плавящимся инконгруэнтно
Химические соединения, при плавлении которых состав образующейся жидкой фазы не совпадает с составом твердой, называют инконгруэнтными или неустойчивыми.
|
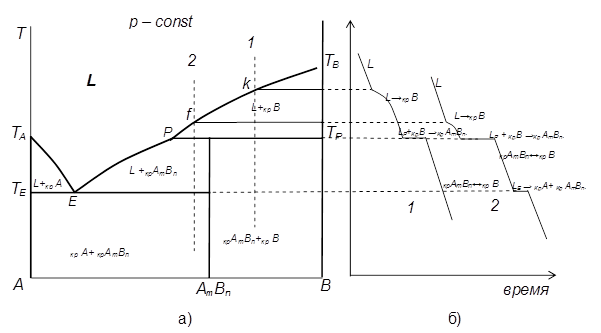
| Рис. 4. 8. Диаграмма плавкости с инконгруэнтно плавящимся химическим соединением АmBn и характерные кривые охлаждения |
Характеристика фазовых равновесий в системе
На рис. 4. 8 представлена диаграмма плавкости с инконгруэнтно плавящимся соединением АmBn, имеющим постоянный состав. Взаимная растворимость компонентов А и В в твердом состоянии отсутствует.
Плавление инконгруэнтного соединения происходит с разложением аналогичным перитектическому превращению, т. е. при плавлении неустойчивых соединений, помимо жидкости образуется новая твердая фаза.
Данная диаграмма имеет две линии, отвечающие трехфазному нонвариантному равновесию – это перитектическая и эвтектическая горизонтали.
РТР – линия перитектики или линия разложения химического соединения АmBn при температуре Тр. Эту температуру также называют температурой разложения химического соединения.
На линии разложения в равновесии находятся кристаллы АmBn, кристаллы В и жидкий раствор состава, обозначенного точкой Р. Перитектическое равновесие можно выразить уравнением:
| LР + Кр. В ↔ КрАmBn |
На линии эвтектики при температуре ТЕ, находятся в равновесии три фазы: эвтектический расплав (точка Е ), кристаллы вещества А и кристаллы химического соединения АmBn. Эвтектическое равновесие можно выразить уравнением:
| LЕ ↔ Кр. А + Кр АmBn. |
\
Фазовые превращения в системах с инконгруэнтным химическим соединением
|
|
|
Рассмотрим кристаллизацию некоторых сплавов (рис. 4. 8а, б).
Сплав 1 начинает кристаллизоваться в точке k, выпадают первые кристаллы вещества В. На кривой охлаждения 1 (рис. 4. 8б) появляется излом. Эта двухфазная кристаллизация L→ крВ происходит до температуры разложения ТР.
При температуре ТР начинается перитектическая трехфазная реакция ( Ф=3, С=0 ): LР+Кр. В→ КрАmBn . Из расплава и кристаллов В образуется химическое соединение А mBn. Температура остается постоянной пока не исчезнет вся жидкая фаза. На кривой охлаждения появляется горизонтальный участок.
В результате в системе остается двухфазная механическая смесь кристаллов В и кристаллов соединения А mBn ( Ф=2, С=1 ). Эта смесь в дальнейшем охлаждается без изменений, на кривой охлаждения - плавное уменьшение температуры.
Сплав 2 начинает кристаллизоваться в точке f, так же выпадают кристаллы вещества В и на кривой охлаждения 2 появляется характерный излом. Эта двухфазная кристаллизация L→ крВ происходит до температуры разложения ТР.
При температуре ТР начинается перитектическая трехфазная реакция ( Ф=3, С=0 ): LР+Кр. В→ КрАmBn . Из расплава и кристаллов В образуется химическое соединение А mBn. Температура остается постоянной, пока не исчезнут все кристаллы вещества В. На кривой охлаждения появляется горизонтальный участок.
В системе остается две фазы: жидкость и кристаллы соединения АmBn ( Ф=2, С=1 ). Дальнейшее охлаждение системы приводит к выпадению кристаллов химического соединения L→ крАmBn , жидкость обогащается компонентом А и ее состав смещается по линии ликвидус РЕ до эвтектического в точке Е. На кривой охлаждения равномерное уменьшение температуры.
При достижении температуры эвтектики ТЕ из жидкости эвтектического состава LЕ начинают одновременно выпадать кристаллы чистого вещества А и кристаллы химического соединения А mBn . . При постоянной температуре протекает эвтектическая реакция:
|
|
|
| LЕ → Кр. А + Кр АmBn. |
Система снова становиться трехфазной и нонвариантной ( Ф=3, С=0 ), на кривой охлаждения образуется второй горизонтальный участок.
После исчезновения жидкой эвтектики, данная система охлаждается без изменений как двухфазная механическая смесь Кр. А + КрА mBn.
4. 3. Построение термодинамическим методом основных типов диаграмм плавкости
Набор концентрационных кривых G – xi при различных температурах с определением по ним состава равновесных фаз, позволяет установить характер фазового равновесия в системе и полностью отобразить диаграмму состояния.
Необходимо отметить, что в данном случае речь идет не о строгом расчете, а о построении термодинамическим методом принципиальной схемы, отражающей фазовые равновесия в рассматриваемых системах, при условии, что общий характер взаимодействия в системах в принципе известен.
Диаграммы плавкости с неограниченной растворимостью компонентов в твердом и жидком состояниях
На рис. 4. 9. представлена принципиальная схема построения диаграммы с неограниченной растворимостью.
Температуры плавления компонентов А и В известны и нанесены на диаграмму Т–хi (ТА< ТВ). Расчет и построение концентрационных кривых G–xi , по которым определяют составы сосуществующих равновесных фаз, проводят при различных температурах. Выберем температуры Т1 и Т2, которые лежат между температурами ТА и ТВ, а также температуру Т3> ТВ .

|
| Рис. 4. 9. |
|
|
Вычислим и отметим на графике G–xi свободные энергии Гиббса чистых компонентов А и В: GAL и GВL - для жидкого состояния компонентов, а также GAS и GВS - для твердого состояния компонентов при данной температуре.
Напомним, что стабильной является фаза, для которой изобарно-изотермический потенциал (свободная энергия Гиббса) располагается в области более низких значений. При температуре ТА < Т1 < ТВ компонент А находится в жидкой фазе, поэтому GAL< GAS, а компонент В – в твердой фазе и GВL> GВS.
|
|
|
Учитывая общий характер концентрационной зависимости изобарно-изотермического потенциала для растворов, соединяем соответствующими кривыми попарно точки GAL и GВL, а также GAS и GВS. В итоге получаем при температуре Т1 две пересекающиеся кривые GL - для жидких и GS - для твердых растворов.
Проводим общую касательную к этим кривым и в точках касания ℓ 1 и s1, получаем составы хВL и хВS соответственно жидкой и твердой фаз, находящихся в равновесии при температуре Т1.
Далее проецируем эти составы на диаграмму состояния Т–хi на горизонталь Т1, обозначенную на рисунке. В результате получаем конноду ℓ 1 s1, концы которой отвечают составам насыщенных жидких и твердых растворов, находящихся в равновесии при Т1 .
Повторяя ход рассуждений для любой другой температуры, например Т2, можно получить другую пару сопряженных точек ℓ 2 и s2 на изотерме Т2 диаграммы состояния.
Т. к. Т2 > Т1 концентрационные кривые располагаются в области более низких значений.
При температуре Т3 , выбранной выше температур плавления компонентов, термодинамически устойчивым будет жидкий раствор во всем диапазоне концентраций ( GL< GS ). Следовательно, концентрационная зависимость GL будет располагаться ниже кривой GS для твердых растворов и общую касательную к этим кривым провести нельзя. Кристаллизация твердого раствора невозможна.
Соединим на диаграмме Т–хi общей кривой все точки ℓ i, отвечающие жидким растворам, включая ТА и ТВ, получаем кривую ликвидус. Соответственно кривая, соединяющая точки si - линия солидус. Замыкая эти кривые в точках плавления компонентов, получаем простейший вариант фазовой диаграммы, характеризующий равновесие двух фаз.
Диаграммы плавкости с простой эвтектикой, компоненты которой не растворимы в твердом состоянии
На рис. 4. 10 представлена принципиальная схема построения диаграммы с отсутствием растворимости в твердом состоянии эвтектического типа.
Напомним, что в системах с эвтектикой компоненты А и В не образуют твердых растворов и кристаллизуются раздельно. В твердом состоянии сплавы этой системы представляют собой механическую смесь двух твердых кристаллических фаз кр. А и кр. В. Поэтому концентрационная зависимость GS–xi для твердой смеси представляет собой аддитивную прямую GSмех. смеси или, если кристаллизуется один компонент, рассматриваем энергию Гиббса чистых твердых компонентов GAS или GВS .
|
|
|
В жидком состоянии компоненты этой системы растворимы неограниченно, что характеризуется концентрационной кривой GL, обращенной выпуклостью вниз.
Температуры плавления чистых компонентов ТА и ТВ известны и отмечены на диаграмме Т–хi. Исходя из характера фазовых равновесий в данной системе, выберем температуры, при которых будут строиться концентрационные зависимости G–xi. Интервал температур: от Т1 – это температура выше Тпл . тугоплавкого компонента, до температуры Т5, которая лежит ниже самого низкотемпературного фазового превращения. Промежуточные температуры соответствуют различным фазовым равновесиям.
Выбранные температуры Т1, Т2, Т3, Т4 и Т5 отметим на диаграмме состояния и проведем для них изотермы.
Для выбранных температур строят концентрационные зависимости G–xi и определяют составы равновесных фаз.

|
| Рис. 4. 10. |
Температура Т1.
Отметим энергии Гиббса чистых компонентов GAL и GВL для жидкого состояния, а также GAS и GВS – для твердого. Кристаллы обоих компонентов являются неустойчивыми, т. к. GAL< GA S и GВL< GВS. Соединяем попарно точки GAL и GВL кривой жидких растворов GL, а точки GAS и GВS – аддитивной прямой GSмех. смеси.
Кривая GL располагается ниже во всем диапазоне концентраций, стабильно существует только жидкий раствор.
При температуре Т2 ( ТА> Т2> ТВ ) для чистых компонентов GAL> GAS, а GВL< GВS . Кристаллическая фаза компонента А становится более устойчивой, компонент В пока находится в жидкой фазе.
Соединяем точки GAL и GВL кривой жидких растворов GL. Чтобы найти состав раствора, находящегося в равновесии с кристаллами вещества А, проводим касательную из точки GAS к кривой GL. Точка касания ℓ 2 дает состав жидкого насыщенного раствора при температуре Т2.
Проецируем этот состав на диаграмму состояния Т–хi на горизонталь Т2. Получаем конноду, на которой точка ℓ 2 отвечает насыщенному жидкому раствору, находящемуся в равновесии с кристаллами чистого вещества А при Т2.
При температуре Т3 ( ТЕ< Т3< ТА, ТВ ) для чистых компонентов GAL> GAS и GВL> GВS. Устойчивы обе кристаллические фазы и компонента А и компонента В.
Соединяем точки GAL и GВL кривой GL. Чтобы найти составы растворов, находящиеся в равновесии с кристаллами вещества А и с кристаллами вещества В , проводим соответственно две касательные из точки GAS и из точки GВS к кривой GL. Точки касания дают составы жидких насыщенных растворов при температуре Т3.
|
|
|
Проецируем эти составы на диаграмму состояния Т–хi на горизонталь Т3. Получаем точки ℓ 3 и ℓ 3´ , которые отвечают насыщенным жидким растворам, находящимся в равновесии с кристаллами А и В соответственно.
При эвтектической температуре Т4=ТЕ выполняется трехфазное равновесие LE↔ Кр. А+Кр. В, начинает кристаллизоваться механическая смесь. Прямая GSмех. смеси имеют точку касания е с кривой GL на составе, характеризующей точку эвтектики.
Проецируем эту точку жидкой эвтектики на горизонталь Т4.
При температуре Т5 устойчивой является твердая механическая смесь кристаллов А и В. GSмех. смеси расположена ниже кривой GL. Жидкие растворы при этой температуре термодинамически неустойчивы.
Далее соединяем точки ТА, ℓ 2, ℓ 3, е на диаграмме Т–хi левой линией ликвидус. Точки ТВ, ℓ 3´ , е – правой линией ликвидуса. Пересекаются линии в точке е , лежащей на линии эвтектики.
Диаграммы плавкости с ограниченной растворимостью компонентов в твердом состоянии эвтектического типа
На рис. 4. 11. представлена схема построения диаграммы указанного типа для некоторых характерных температур.
Аналогично предыдущему типу диаграмм заранее отмечают температуры плавления ТА и ТВ на диаграмме Т–хi. Выбирают температуры Т1, Т2 и Т3 для расчета и построения концентрационных зависимостей свободных энергий Гиббса. Выбранные температуры отмечают изотермами на диаграмме Т – хi.
Для этих температур строят концентрационные зависимости G – xi и определяют составы равновесных фаз.
На диаграммах G–xi для каждого из трех присутствующих в системе растворов имеется своя кривая изобарно–изотермического потенциала: для жидких расплавов – это GL и для двух твердых растворов: Gα S на основе компонента А и Gβ S на основе компонента В соответственно.
Отметим, что кривая GL для жидких растворов существует во всем диапазоне концентраций (растворимость неограниченная).
Так как твердые растворы стабильны только вблизи чистых компонентов (растворимость ограниченная), то кривой Gα S ограничимся в области компонента А и Gβ S - в области компонента В.
Температура Т1. Отметим энергии Гиббса чистых компонентов GAL и GВL в жидком состоянии, а также GAS и GВS для твердого состояния. GAS< GAL и GВS< GВL . Напомним, что стабильная фаза имеет более низкое значение термодинамического потенциала при данной температуре.
Соединяем точки GAL и GВL кривой GL, характеризующей жидкие растворы. Жидкая фаза при данной температуре является неустойчивой, кривая GL лежит в области достаточно высоких значений энергии Гиббса.
Кривые для твердых растворов Gα S и Gβ S расположены ниже и к ним можно провести общую касательную, что свидетельствует о равновесии двух твердых растворов α ↔ β . Составы равновесных фаз устанавливаются точками касания а1 и b1 и проецируются на горизонталь при температуре Т1 на диаграмме Т – хi .

|
| Рис. 4. 11. |
При температуре Т2=ТЕ наблюдается трехфазное эвтектическое равновесие: LE↔ α Е+β Е. Это значит, что химические потенциалы обоих компонентов равны во всех трех фазах, т. е. μ АL=μ Аα =μ Аβ и μ ВL=μ Вα =μ Вβ .
Геометрической интерпретацией такого равновесия является то, что общую касательную можно провести ко всем трем кривым GL, Gα S и Gβ S. Точки касания а2 , е, b2 устанавливают составы равновесных фаз, а проецирование этих составов на диаграмму Т–хi к температуре ТЕ позволяет установить фиксированное положение эвтектической горизонтали.
При температуре Т3 кривая для жидкой фазы смещается вниз. К этим кривым можно попарно провести две касательные.
Касательная к кривым GL и Gα S свидетельствует о существовании равновесия L↔ α ; касательная к кривым GL и Gβ S характеризует равновесие L↔ β.
Проецируем попарно точки касания а3 и ℓ 3, а также ℓ 3´ и b3 на изотерму Т3.
Далее, на диаграмме Т–хi через точки характеризующие жидкие растворы, проводим ветви ликвидуса, соединяя их в точке эвтектики е, а через точки характеризующие твердые растворы - две ветви солидус, заканчивая их в точках а2 и b2 на линии эвтектики. Точки а1 и b1 лежат на линии ограниченной растворимости.
Диаграммы плавкости с ограниченной растворимостью компонентов в твердом состоянии перитектического типа
Схема построения данной диаграммы представлена на рис. 4. 12. Она во многом аналогична предыдущей (см. рис. 4. 11).
Эвтектические и перитектические превращения являются типичными примерами нонвариантных равновесий в двойных сплавах с ограниченной растворимостью.
На диаграммах термодинамического потенциала, так же как в предыдущем случае, имеется своя кривая для каждой из трех фаз: для жидких расплавов - это GL; и для двух твердых растворов: Gα S - для твердого раствора на основе компонента А и Gβ S - для твердого раствора на основе компонента В соответственно.
При температуре Т1 к концентрационным кривым термодинамических потенциалов можно попарно провести две касательные.
Касательная к кривым GL и Gα S свидетельствует о существовании равновесия L↔ α ; касательная к кривым Gα S и Gβ S характеризует равновесие α ↔ β . Проектируем попарно точки касания на изотерму Т1.

|
| Рис. 4. 12. |
При температуре Т2 , равной температуре перитектики ТР, наблюдается трехфазное равновесие LР +β Р↔ α Р. Общую касательную можно провести ко всем трем кривым GL, Gα S и Gβ S.
Точки касания устанавливают составы соответствующих равновесных фаз, а проецирование этих составов на диаграмму Т–хi к температуре ТР позволяет установить фиксированное положение перитектической горизонтали.
При температуре Т3 касательная к кривым GL и Gβ S свидетельствует о фазовом равновесии L↔ β . Фаза твердых растворов Gα S неустойчива, эта кривая расположена выше и к ней нельзя провести касательной.
|
|
|


