Моделирование СМО с отказами по схеме процессов

Напомним, что рассматривается СМО с отказами (т.е. без буфера), имеющая два обслуживающих прибора. Интервал t между заявками распределен по экспоненциальному закону с математическим ожиданием m_t. Время обслуживания t_обсл постоянно. Оценивается вероятность потери заявки Р_пот, распределение числа занятых приборов (Р₀, Р₁, Р₂) и коэффициент загрузки прибора Р_зп. Обозначения будут те же, что в алгоритме из раздела 2.3.1, и немного добавлено: К_сп,- количество свободных приборов, К - максимальное число одновременно существующих процессов (емкость календаря) и др. Календарь теперь указывает не моменты наступления событий, а моменты активизации процессов. Активизацией процесса называется выполнение алгоритма, соответствующего очередной фазе этого процесса. Календарь содержит и момент активизации процесса Т(J) и метку очередной его фазы M(J), где J -номер процесса (J=f,...,K).

В приведенном ниже алгоритме первая цифра метки соответствует номеру процесса, а вторая - номеру фазы в этом процессе.

 

Моделирование СМО с отказами по схеме процессов

 

ввод данных (m_t, t_обсл, правило остановки)

установка начальных значений переменных, в том числе заполнение календаря (N:=0, Т_T:=0, К_З:=0, К_ПОТ:=0,

S₀:=0, S₁:=0, S₂:=0, T(J)=0,

J=1..K; M(1):=11; M(J):=0, J:=2..K, K_СП:=2)

do шаг имитации (раскрыт ниже)

until выполнено условие остановки

End - do

вычисление оценок

выдача результатов

end -моделир.

 

Шаг имитации

увеличение номера шага (N:=N+1)

запоминание особого момента (T_L:=T_T)

определение очередного особого момента (Тт:= minT(J)|M(J)¹0)

пополнение суммарного времени пребывания в определенном состоянии (y:=2-K_СП; ДТ:=Т_Т-Т_L; Sy:= Sy +ДT)

установка текущего номера процесса в нуль (J_Т: = 0)

do определение очередного номера процесса (J_T:=J_T+1)

подъем флага (IFL:= 1)

if процесс с номером J_T существует (М(J_T)¹0)

then if запланированный момент активизации совпадает с текущим моментом (T(J_Т=T_Т)

then имитация процесса о номером J_Т, начиная с фазы

М(J_Т) до тех пор, пока это возможно по алгоритму соответствующего класса

End if

End if

if флаг сбросился (IFL = 0)

then возврат к началу списка процессов (J_Т:= 0)

End if

until просмотрен и, если надо, имитирован последний процесс, а флагостался

поднятым (J_Т=K & IFL =1)

End do

end шаг

 

Класс процессов "генерирование заявок источником"

{предполагается единственный источник бесконечной емкости)

(11) подготовка заявки в течение времени t:

генерирование интервала t (обращение к датчику случайных

чисел, реализующему экспоненциальное распределение с мате-

матическим ожиданием m_t)

планирование выдачи заявки источником (T(1):=T(1)+ t;

M(1):=12 {процесс этого класса существует постоянно,

причем в единственном числе; поэтому ему постоянно

отведена группа под номером 1}

(12) создание процесса "прохождение заявки":

поиск свободной группы и присваивание ее номера перемен

ной Jv {группа с номером J свободна, если M(J)=0}

создание процесса под номером Jv (T(Jv):=T(1); M(Jv):=21)

пополнение счетчика заявок (Kз:=Kз+1)

установка указателя активной фазы на начало процесса

(М(1):=11))

end класс "ГЗИ"

 

Класс процессов "прохождение заявки"

переход к запланированной фазе (goto М (.Jт))

(21) занятие прибора:

if есть свободный прибор (Кcп>0)

then занятие прибора (Ксп:=Кcп-1),

установка на обслужи вание (М(Jт):=22)

else потеря заявки (Кпот:=Кпот+1),

установка на ликвидацию процесса (M(Jт):=24)

End if

переход к соответствующей фазе (gо to М Jт))

(22) обслуживание заявки в течение времени t_обсл:

планирование освобождение прибора (Т(Jт):=Т(Jт)+t_обсл)

прерывание до наступления запланированного момента (goto end класс"ПЗ")

[23) освобождение прибора:

увеличение числа свободных приборов (Ксп:= Ксп+1)

сброс флага (lFL:= 0)

(24) ликвидация процесса (M(Jт):=0)

end класс"ПЗ"

 

Сопоставим схему событий и схему процессов, так как их можно считать конкурирующими.

Схема событий более стройна: события не пересекаются, за один шаг имитируется одно событие, события имитируется в хронологическом порядке, алгоритм шага делится на этапы с четким функциональным назначением (имитация события, пополнение статистик, планирование новых событий). Однако в сложных ситуациях довольно трудно сформировать перечень типов событий и правильно разработать соответствующие им части алгоритма.

С этой точки зрения схема процессов удобнее, так как не требует при разработке алгоритма учитывать сразу все, что может происходить в системе, а допускает раздельную разработку отдельных процессов. Особенно упрощается разработка имитационных моделей при использовании универсальной системы моделирования, когда пользователю требуется только описать последовательность событий и работ в процессах, а учет взаимодействия процессов, сбор статистики, управление порядком имитации процессов берет на себя система моделирования. Схема процессов не позволяет выделить функционально различные части алгоритма: пополнение статистик и планирование событий исследуют с операциями смены состояний в рамках одной фазы процесса. Это чревато упущениями при разработке алгоритма.

 

 

Численный пример

Дополним приведенное сопоставление этих двух схем построения моделирующего алгоритма количественной характеристикой на примере модели виртуального канала (ВК).

ВК представляет собой коммутационный канал, обеспечивающий транспортировку пакетов между двумя портами сети, т. е. является некоторым маршрутом в сети (рис. 1), состоящим из последовательности n узлов коммутации (УК) и (n-1) КС, по которому осуществляется передача информации из узла источника УК1 в узел - адресат УКn.

Рис. 1. Структура модели виртуального канала

Особенностью имитационной модели ВК является отображение фоновых потоков, циркулирующих по сети и влияющих на процесс прохождения пакетов по выделенному (моделируемому) пути.

Узлы в моделирующей программе ВК представляются тремя модулями. Первый обеспечивает возникновение требований к передаче пакетов; второй реализует коммутацию пакетов; третий – передачу пакетов следующему узлу.

Положим, пакет выделенного потока поступил в устройство в момент , и спланирован момент очередного следующего поступления пакета выделенного потока через интервал y.

Интервалы между поступлениями пакетов выделенного потока есть реализации случайной величины, распределенной экспоненциально с параметром .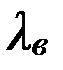

Помимо выделенного потока на тот же вход устройства поступает фоновый пуассоновский поток с параметром .

В календаре событий записываются моменты времени поступлений транзактов обоих потоков.

Если за интервал y между моментами и поступлений транзактов выделенного потока не поступало транзактов фонового потока, то для продвижения транзакта (взятия на обслуживание, постановки в очередь и т.п.) потребуется однократное обращение к календарю. Вероятность отсутствия поступления транзактов фонового потока на интервале (, ) есть

P(1) =

Соответственно, если на интервал (, ) постает n транзактов фонового потока, моменты поступлений которых опережают момент , то в такой ситуации для продвижения транзакта выделенного потока потребуется (n + 1) обращений к календарю. Вероятность такого количества обращений есть

P(n +1)=

Условное математическое ожидании числа обращений к календарю для продвижения одного транзакта выделенного потока в одном устройстве при наличии фонового потока определим как

Усредняя по y, получим окончательно среднее значения числа обращений к календарю для продвижения одного транзакта выделенного потока в одном устройстве при наличии фонового потока

(1)

Положим, типовая операция продвижения транзактов выделенного потока осуществляется в многофазной системе, каковой является модель виртуального канала. Пусть модель включает N узлов. Тогда виртуальный календарь такой многофазной системы будет содержать

g = (2)

мест для записи особых моментов. Полагаем, что относящиеся к отдельному какому – либо узлу (узлы считаем идентичными) моменты особых состояний распределены равновероятно в ряде общих мест календаря. Тогда среднее число обращений к общему календарю, обеспечивающее выборку i = = значений, можно оценить формулой

(3)

Итак, при продвижении транзакта выделенного потока в отдельном узле многофазной системы, состоящей из N узлов, оценку среднего числа обращений к общему календарю при построении алгоритма моделирования по схеме событий даетформула (3) и, соответственно, формула (1) при построении алгоритма моделирования по схеме процессов. Соотношение этих средних

можно рассматривать как частный количественный критерий эффективности одной схемы построения алгоритма моделирования по отношению к другой.

В табл. 1 представлены некоторые численные соотношения анализируемого сопоставления названных схем

Табл. 1. Сопоставление числа обращений к календарю

Число узлов N     Отношение                 Соотношение числа обращений к календарю()   18,9   39,9   68,9   105,9   33,6   71,1   122,8   188,7

 

Таким образом, в имитационной модели, алгоритм которой построен по схеме событий, на каждом очередном шаге выполняется то особое состояние, время наступления которого ближайшее к текущему моменту. При этом на каждом шаге возможен переход к любому из программных модулей, реализующих моделирующий алгоритм. А это, в свою очередь, влечет вызов другой структуры данных, соответствующий типу особого состояния.

Схема процессов обеспечивает переход к нужному модулю и позволяет выполнять несколько последовательных особых состояний при очередном переходе к определенному модулю, что, как показывают приведенные расчеты, существенно сокращает число обращений к календарю событий и тем самым ускоряет процесс моделирования.

Схема процессов удобно реализуется с использованием объектно-ориентированного подхода, который широко применяется при построении мощных инструментальных систем моделирования, как например система AnyLogic.

Подводя итоги, можно оказать, что на этапе начального обучения моделирование и при моделировании простых систем целесообразно применять схему событий, а при моделировании сложных систем с использованием универсальных средств предпочтительнее схема процессов.

 

Вопросы и задания

1. Перечислим отличия схемы событий (СC) от схемы процессов (СП).

СС: В календаре отведены места для событий.. СП:... для процессов.

СС: В календаре для каждого события одна величина (момент события.). СП: В календаре для, каждого процесса две величины (момент активизации и метка фазы).

СС: за один шаг имитируется одно событие. СП: За один шаг имитируется одна или несколько фаз одного или нескольких процессов.

СС: Все объекты существуют постоянно. СП: Возможны временные объекты.

Продолжите этот перечень.

2. В чем состоят преимущества и недостатки схемы процессов по сравнению со схемой событий?

3. Составьте программу моделирования СМО по схеме процессов, реализующую приведенный алгоритм. Убедитесь, что она дает те же средние значения искомых характеристик, что и программа, построенная по схеме событий,

4. Измените алгоритм моделирования СМО так, чтобы он учитывал возможность существования неограниченной очереди к приборам (потерянных заявок не будет). При этом используйте семафор.

5. Сравните по быстродействию три способа организации календаря: простой список, связный список, двусвязный список.

 

 

⇐ Предыдущая891011121314151617Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: