Моделирование случайных событий

 

Случайные события бывают различного типа: простыми и сложными, со­вместными и несовместными, зависимыми и независимыми. Случайные величины – дискретными и непрерывными. Поэтому моделирование случайных событий и величин подразделяется на ряд отдельных процедур в зависимости от условий. Рассмотрим их по мере ус­ложнения.

Моделирование случайного события. Основной характеристикой любого случайного события А является веро­ятность его появления – Р (А). Процедура моделирования простого случайного события А состоит из:

– формирования значения БСВ z_i Î R;

– сравнения z_i с заданной вероятностью Р (А) появления события А. Если условие z_i < P (A) выполняется, то исходом моделирования является событие А. В противном случае - противоположное со­бытие

Алгоритм моделирования отдельных случайных событий имеет вид, приведенный на рис. 7.1.

ziÎR

Фиксируется А

Фиксируется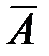

Да

Нет

zi < P (A)

 

 

 

Рис. 7.1. Алгоритм моделирования отдельных случайных событий

Моделирование полной группы несовместных случайных событий. Пусть задано некоторое множество элементарных исходов { A ₁,..., A_n } c их вероятностями p ₁,..., p_n соответственно (p ₁+…+ p_n =1).Чтобы построить программную модель, «оживляющую» такую совокупность исходов, разобьём мысленно интервал значений БСВ (0 £ t £ 1) на n отрезков длиной p ₁, p ₂,..., p_n. Это всегда возможно, так как p ₁+…+ p_n =1. Например, можно определить отрезки так:

 

 

Алгоритм моделирования случайных исходов A_j состоит в том, чтобы, обратившись к датчику БСВ, определить, в какой из интервалов ₁,  ₂,..., _n попало значение БСВ. Факт его попадания в конкретный интервал  _j предопределяет переход алгоритма к процедуре имитации соответствующего, имеющего тот же номер, исхода A_j. Поскольку вероятность попадания БСВ в интервал  _j равна его длине p_j, то и вероятность исхода A_j будет равна p_j. Такой метод моделирования простых независимых событий называют «исход испытания по жребию».

В качестве примера построим модель операции, состоящей в вытаскивании шара из урны, содержащей пять белых шаров (Б), три красных (К) и два черных (Ч). Так как исходы Б, К, Ч имеют вероятности p ₁= 0,5, p ₂ = 0,3 и p ₃= 0,2 соответственно, то интервал (0,1) разбиваем на отрезки (0;0,5), (0,5;0,8) и (0,8;1).

Алгоритм моделирования имеет примерно следующий вид:

1. Получить значение z из датчика БСВ.

2. Если z £ 1/2, вывести "Б", иначе, если z £ 8/10, вывести "К", иначе вывести "Ч".

Вот пример 60-кратного выполнения этого алгоритма на компьютере; мы видим, что частота появления каждого исхода примерно соответствует его вероятности:

БКБКБКБКББКЧБББККББКЧЧББЧЧКББЧБЧББЧБКЧЧБББККББЧКБЧКББЧКБЧББ

Так, исход "Б" здесь появился 31 раз (52% случаев), "К" - 15 раз (25%) и "Ч" - 14 раз (23%).

Моделирование сложных случайных событий. Сложные события являются исходом, зависящим от двух или более простых событий. Модели этого типа рассматриваются для двух случаев: для независимых простых событий и для зависимых простых событий.

Генерирование сложного события, являющегося результатом наблюдения простых независимых случайных событий рассмотрим на при­мере, когда даны два простых события А и В, для которых за­даны вероятности их появления Р (А) и Р (В) соответственно. События как и образуют полные группы несовместных событий, то есть

Возможные исходы совместных испытаний: и соответствующие этим исходам вероятности Эти сложные исходы образуют полную группу независимых событий, т.е. 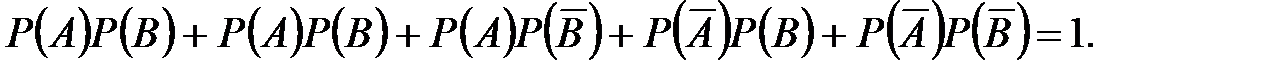Используя эти вероятности и способ «исход испытания по жребию» разыгрываем все возможные исходы.

Второй способ моделирования заключается в поочередном моделирования события А, а затем события В, или, наоборот, сначала В, затем А. Получаем один из четырех приведенных выше исходов.

Генерирование зависимых случайных событий. В тех случаях, когда А и В являются зависимыми событиями, процедура моделирования сложного события выполняется несколько иначе.Исходными данными для модели являются вероятности появления собы­тий А, В и В / А, т.е. соответственно Р (А), Р (В) и Р (В / А) – условная вероятность появления события В при условии, что собы­тие А наступило.

Возможным исходам АВ, А , В, соответствуют вероятности

 

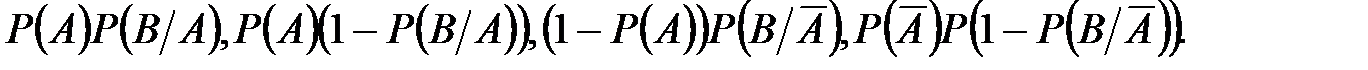(7.3)

 

Условная вероятность находится предварительно из формулы полной вероятности для события В:

Используя вероятности (7.3), разыгрываем возможные реализации сложного события способом «исход испытания по жребию» либо, используя вероятности А, В и В / А, поочередно моделируем события А, а затем события В.

 

⇐ Предыдущая10111213141516171819Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: