Информация как свойство материи

Современное понимание того, что такое информация и какую роль она играет в искусственных и естественных системах, сложилось не сразу; оно представляет собой совокупность знаний, полученных разными науками: физикой, биологией, философией, теорией связи и т.д.

Хотя физика старается изучать явления природы в максимально объ­ек­тивированной (т.е. не связанной с человеком и его воздействием на ок­ру­жающий мир) форме, ей не удалось полностью исключить “че­ло­ве­чес­кий фактор”. Во-первых, при экспериментальном исследовании физических явлений невозможно обойтись без измерения ряда величин, и наличие этих величин в теоретических моделях рано или поздно требует специ­ального рассмотрения того, как именно проводятся измерения – а без влияния человека не проводятся даже автоматические эксперименты. Во-вто­рых, физика не могла не заняться изучением технических (т.е. созданных человеком) устройств и тут-то и “попала в ловушку”: полностью объ­ективистский подход к машинам все равно обнаружил в их поведении следы человеческой деятельности. Впервые это произошло в термоди­намике – науке, изучающей процессы в тепловых машинах. Оказалось, что без введения специального понятия энтропии невозможно дать исчер­пывающего описания их действия. Скачок в по­ни­мании природы этой величины произошел, когда Л.Больцман дал ей статистическую ин­тер­претацию (1877); уже сам Больцман обронил фразу о том, что энтропия характеризует недостающую информацию, но тогда этой фразы никто не понял.

После построения К.Шэнноном теории информации (1948), когда ока­залось, что формула Шэннона для информационной энтропии и фор­му­ла Больцмана для термодинамической энтропии оказались тождес­т­вен­ными, разгорелись споры о том, является ли это совпадение чис­то фор­мальным или оно выражает глубокую связь термодинамики и те­о­рии информации. Дискуссии (в особенности благодаря работам Бриллю­эна [1, 2]) привели к современному пониманию этой неразрывной связи.

Совсем с другой стороны к этой проблеме пришла философская теория познания. Изначальный смысл слова “информация” как “зна­ния, све­дения, сообщения, уведомления, известия, ведомости”, т.е. нечто присущее только человеческому сознанию и общению, начал расширяться и обобщаться. Признав, что наше знание есть отражение реального мира, материалистическая теория познания установила, что отра­жение является всеобщим свойством материи. Сознание человека яв­ля­ется высшей, спе­цифической формой отражения, но существуют и дру­гие формы – пси­хическая (присущая не только человеку, но и живот­ным), раздражимость (охватывающая, кроме того, растения и простейшие организмы) и, наконец, самая элементарная форма – за­пе­чат­ле­ние взаимодействия (при­сущая и неорганической природе, и элементарным частицам, т.е. всей материи вообще). И теперь, как только состояния одного объекта на­ходятся в соответствии с состояниями другого объекта (будь то соот­ветствие между положением стрелки вольтметра и напряжением на его клем­мах или соответствие между нашим ощу­ще­ни­ем и реальностью), мы го­ворим, что один объект отражает дру­гой, содержит информацию о другом.

Так вновь сомкнулись результаты философского и естественнонауч­ного исследования природы. Иначе и быть не могло – ведь предмет изу­чения един, хотя это изучение ведется с разных позиций и разными методами. В настоящее время информация рассматривается как фундаментальное свойство материи.

Таким образом, ясно, что роль информации в самом существовании систем, искусственных и естественных, огромна. Понятие информации, обладая всеобщностью, приобрело смысл философской категории. Для кибернетики, да и всей системологии, понятие информации столь же фундаментально, как понятие энергии для физики. Недаром признается не менее общим, чем определение А.И.Берга (см. гл.1), определение кибернетики, предложенное А.Н.Колмогоровым: кибернетика – это наука, которая занимается изучением систем любой природы, способных воспринимать, хранить и перерабатывать информацию и использовать ее для управления и регулирования.

Подведем итог Исследуя информацию, кибернетика не от­кры­ла нового свойства материи: оно из­вест­но в философии под названием свой­­ства отражения. Новое состоит в том, что ин­формацию можно исследовать ко­ли­чественно.

Summary In studying information, cybernetics has not discovered a new property of matter: it is known in philosophy as the reflection property. What is new is its quantitative study of information.

СИГНАЛЫ В СИСТЕМАХ

Как мы уже отмечали, для того чтобы два объекта содержали информацию друг о друге, необходимо, чтобы между их состояниями существовало соответствие: только при этом условии по состоянию одного объекта можно судить о состоянии другого. Такое соответствие может установиться только в результате физического взаимодействия между этими объектами. Редко бывает, чтобы два объекта взаимодействовали “не­посредственно”: даже между печатью и документом нужен слой мастики; сквозь кинопленку до экрана проносится пучок света; от речевого аппарата оратора до ушей слушателей звук переносится колебаниями воздуха. Другими словами, соответствие между состояниями двух объектов может устанавливаться и с помощью взаимодействия с промежуточными объектами, часто даже целой совокупностью промежуточных объектов.

ПОНЯТИЕ СИГНАЛА

Итак, сигнал есть материальный носитель информации, средство перенесения информации в пространстве и времени.

Утверждая что объекты выступают в качестве сигналов, мы должны сделать уточнение. Один и тот же объект может “выступать в качестве” разных сигналов: колебания воздуха могут нести звуки музыки, речь лектора, пение птиц или шум самолета; с магнитной ленты можно стереть одну запись и сделать другую и т.д. Следовательно, в качестве сигналов используются не сами по себе объекты, а их состояния.

Далее, не всякое состояние имеет сигнальные свойства. Точнее го­во­ря, данный объект взаимодействует не только с тем объектом, информа­цию о котором мы хотели бы получить, но и с другими, не интересую­щи­ми нас объектами. В результате соответствие состояний ослабевает, раз­рушается. Условия, обеспечивающие установление и спо­собствующие со­хранению сигнального соответствия состояний, называются кодом*. По­сторонние воздействия, нарушающие это соот­ветствие, называются по­мехами или шумами. Нарушение соответствия может происходить не только вследствие помех, но и из-за рассогласования кодов вза­и­мо­дей­ствующих объектов. В искусственных системах, где такое согласование ор­ганизуется специально, это явно видно на примере криптографии, ос­но­ванной на засекречивании кодов. В природных системах согласование ко­дов происходит в самой структуре систем через естественный отбор различных вариантов.

ТИПЫ СИГНАЛОВ

Поскольку сигналы служат для переноса ин­формации в пространстве и времени, для обра­зования сигналов могут использоваться только объекты, состояния которых достаточно ус­той­чивы по отношению к течению времени или к изменению положения в пространстве. С этой точки зрения сигналы делятся на два типа.

INFORMATION информация BEARER HOLDER носитель INTERFERENCE помехи SIGNAL сигнал     Информация есть свойство материи, состоящее в том, что в результате взаимодействия объектов между их состояниями устанавливается определенное соответствие. Чем сильнее выражено это соответствие, тем полнее состояние одного объекта отражает состояние другого объекта, тем больше информации один объект содержит о другом. Сигнал есть материальный носитель информации. В качестве сигналов используются состояния физических объектов или полей. Соответствие между сигналом и несомой им информацией устанавливается по специальным правилам, называемым кодом.

К первому типу относятся сигналы, являющиеся стабильными состояниями физических объектов (например, книга, фотография, магнитофонная запись, состояние памяти ЭВМ, положение триангуляционной вышки и т.д.). Такие сигналы называются статическими.

Ко второму типу относятся сигналы, в качестве которых используются динамические сос­то­яния силовых полей. Такие поля характеризуют­ся тем, что изменение их состояния не может быть локализовано в (неизолированной) части по­ля и приводит к распространению возмущения. Конфигурация этого возмущения во время рас­пространения обладает определенной устойчи­востью, что обеспечивает сохранение сигналь­ных свойств. Примерами таких сигналов могут слу­жить звуки (изменение состояния поля сил уп­ругости в газе, жидкости или твердом теле), све­товые и радиосигналы (изменения состояния элек­тромагнитного поля). Сигналы ука­зан­ного типа называются динамическими *.

Понятно, что динамические сигналы использу­ются преимущественно для передачи, а статиче­ские – для хранения информации, но можно най­ти и противоположные примеры (ди­на­ми­че­ские запоминающие устройства, письма, газеты).

—————————— * Обратим еще раз внимание на относительность вся- кой классификации. К какому из введенных классов вы отнесете дымовые сигналы, или запах, или голо- графическое изображение?

Сигналы играют в системах особую, очень важную роль. Если энергетические и вещественные потоки, образно говоря, питают систему, то потоки информации, переносимые сигналами, организуют все ее функционирование, управляют ею. Н.Винер, например, подчеркивал, что общество простирается до тех пределов, до каких распространяется информация. Пожалуй, это следует отнести к любой системе.

Подведем итог Первое и, быть может, главное отличие под­хода к изучению любого объекта как сис­темы, а не как просто объекта, и состо­ит в том, что мы ограничиваемся не только рассмотрением и описанием вещест­вен­ной и энергетической его сторон, но и (преж­де всего) проводим исследование его информационных аспектов: целей, сиг­на­лов, информационных потоков, управле­ния, организации и т.д.

Summary The first and perhaps the main distinction of the approach to studying an object as a system, and not just as a mere object, is that we do not restrict ourselves to studying and describing it only in terms of substance and energy, but also (and preferably) from the standpoint of information: its purposes, signals, information flows, control, organization, etc.

§ 5.3. СЛУЧАЙНЫЙ ПРОЦЕСС – МАТЕМАТИЧЕСКАЯ
МОДЕЛЬ СИГНАЛОВ

Казалось бы, после того как мы установили, что сигналами служат состо­яния физических объектов, никаких проблем с их математическим опи­санием не должно быть: ведь физика имеет богатый опыт построения ма­тематических моделей физических процессов и объектов. Например, мож­но зафиксировать звуковые колебания, соответствующие конкретно­му сигналу, в виде зависимости давления x от времени t и изобразить этот сигнал функцией x (t); такой же функцией можно изобразить и стати­ческий сигнал, например запись этого звука на магнитной ленте или на грампластинке, поставив параметру t в соответствие протяженность (длину) записи.

НЕПРЕДСКАЗУЕМОСТЬ – ОСНОВНОЕ СВОЙСТВО СИГНАЛОВ

Однако имеется существенное различие между просто состоянием x (t) объекта и сигналом x (t). Оно состоит в том, что единственная функция x (t) не исчерпывает всех важных свойств сигналов. Ведь понятие функции предполагает, что нам известно значение x (либо правило его вычисления) для каждого t. Если же это известно получателю сигнала, то отпадает необходимость в передаче: функция x (t) может быть и без этого воспроизведена на приемном конце.

Следовательно, единственная однозначная функция вещественного ар­гумента не может служить моделью сигнала. Такая функция приобрета­ет сигнальные свойства только тогда, когда она является одной из возмож­ных функций. Другими словами, моделью сигнала может быть набор (или, как еще говорят, ансамбль) функций па­раметра t, причем до передачи неизвестно, ка­кая из них будет отправлена; это становится из­вест­ным получателю только после передачи. Каж­дая такая конкретная функция называется ре­ализацией. Если теперь еще ввести вероятност­ную меру на множество реализаций, то мы по­лучим математическую модель, называемую слу­чайным процессом *.

RANDOM случайный NOISE шум OSCILLATION колебание ENVELOPE огибающая   Случайный процесс хорошо отображает главное свойство реальных сигналов – их неизвестность до момента приема. Однако некоторые модели обладают и “лишними”, не присущими реальным сигналам свойствами. Напри- мер, описание реализаций случайного процесса аналитическими функциями предполагает бесконечную точность, чего в реальности не бывает.

—————————— * Изложение будет вестись в предположении, что читателю знакомы элементы теории вероятностей.

Прежде чем перейти к некоторым подробностям этой модели, отметим, что у нее все-таки имеются качества, которых нет у реальных сигналов (еще раз обратим внимание на нетождественность модели и оригинала). Дело в том, что реальные системы всегда оперируют только с конечным объемом данных, а понятие аналитической функции предполагает ее точное значение для каждого значения аргумента, т.е. такое, которое может быть представлено только с помощью бесконечного ряда цифр. Иначе говоря, в “более правильной” модели сигнала любая реализация не должна определяться с бесконечной точностью. Но пока не существует подходящего математического аппарата, столь же удобного, как математический анализ, и мы вынуждены пользоваться традиционным понятием функции. Это сопряжено с тем, что в выводах теории могут появиться (и на самом деле появляются [6]) парадоксы, природа которых связана не с реальными сигналами, а с их моделью. Во всяком случае, там, где конечная точность реальных сигналов существенна для самой постановки задачи, ее вводят в модель либо как добавочный “шум”, либо как “квантование” непрерывного сигнала (наподобие шкалы с делениями у измерительных приборов).

Вернемся к рассмотрению случайных процессов как моделей сигна­лов. Имеется несколько различных подходов к тому, как вводить вероят­ностную меру на множестве реализаций. Для инженерных приложений ока­зывается удобным определение случайного процесса как такой функ­ции времени x (t), значение которой в каждый данный момент является случайной величиной. Случайная величина полностью характеризуется распределением вероятностей, например плотностью P ₁(x ₁ | t ₁); однако, чтобы охарактеризовать случайный процесс, нужно описать, связаны ли (и если да, то как) значения реализации, разделенные некоторыми интервалами времени. Так как связь только двух таких значений, описываемая распределением второго порядка P ₂(x ₁, x ₂ | t ₁, t ₂), может неполно характеризовать процесс в целом, вводят распределения третьего, четвертого,..., n -го порядков: Р_n (x ₁,..., x _n | t ₁,..., t_n). В конкретных задачах обычно ясно, до какого порядка следует доходить в описании процесса.

КЛАССЫ СЛУЧАЙНЫХ ПРОЦЕССОВ

Необходимость моделирования самых разнообразных сигналов приводит к построению частных моделей случайных процессов, т.е. наложению дополнительных ограничений на параметры распределений и на сами распределения. Перечислим наиболее важные классы случайных процессов.

Непрерывные и дискретные по времени процессы. Случайный процесс с непрерывным временем характеризуется тем, что его реализации определяются для всех моментов из некоторого (конечного или бесконечного) интервала T параметра t. Дискретный по времени процесс* задается на дискретном ряде точек временной оси (обычно равноотстоящих).

Непрерывные и дискретные по информативному параметру процессы. Эти процессы различаются в зависимости от того, из какого (непрерывного или дискретного) множества принимает значение реализация x случайной величины X.

Стационарные и нестационарные процессы. Так называются процессы в зависимости от постоянства или изменчивости их статистических характеристик. Случайный процесс называется стационарным в узком смысле, если для любого n конечномерные распределения вероятностей не изменяются со временем, т.е. при любом? выполняется условие

P_n (x ₁,..., x_n | t ₁ +?, t ₂ +?,..., t_n +?) = P_n (x ₁,..., x_n | t ₁, t ₂,..., t_n).

Если же условие независимости от времени выполняется только для первых двух моментов (среднего и функции автокорреляции), то процесс называется стационарным в широком смысле (или в смысле Хинчина).

Эргодические и неэргодические процессы. На практике при описании случайных величин вместо рассмотрения их распределений часто ограничиваются только их числовыми характеристиками, обычно моментами. В тех случаях, когда распределение неизвестно, моменты (и другие числовые характеристики) можно оценить статистически.

Перенос такой практики на произвольные случайные процессы требует не только учета зависимости отстоящих друг от друга (“разнесенных”) во времени значений, но и наложения дополнительных требований. Требование совпадения величин, получающихся при усреднении по ансамблю (т.е. при фиксированном времени) и при усреднении по времени (точнее, по одной реализации), и называется условием эргодичности. Это требование можно толковать и как совпадение результатов усреднения по любой реализации*. Как и для стационарности, можно различать эргодичность в узком и широком смысле.

Можно продолжать классификацию случайных процессов и дальше, но мы будем делать это при рассмотрении конкретных вопросов.

Подведем итог Основной результат данного параграфа состоит в том, что случайный процесс может служить математической моделью сигнала. Необходимо только следить за тем, чтобы конкретные особенности изучаемых сигналов были корректно отображены в свойствах случайного процесса.

Summary The gist of this section is the conclusion that a random process can be used as a mathematical model of a signal. But it is necessary to pay special attention to the correctness of mapping characteristics of the studied signals onto properties of the random process.

§ 5.4. МАТЕМАТИЧЕСКИЕ МОДЕЛИ РЕАЛИЗАЦИЙ
СЛУЧАЙНЫХ ПРОЦЕССОВ

Для рассмотрения конкретных свойств систем бывает необходимо учесть особенности сигналов, циркулирующих по каналам связи этих систем. Такие особенности можно описать по-разному: просто перечислить возможные реализации (если число их конечно) либо задать в той или иной форме общие свойства реализаций, входящих в ансамбль. О дискретных процессах мы будем говорить отдельно (см. § 5.8), а сейчас рассмотрим математические модели реализаций непрерывных сигналов.

Приведем примеры, с которыми часто имеют дело в теории сигналов [7].

МОДЕЛИРОВАНИЕ КОНКРЕТНЫХ Реализаций

Гармонические сигналы. Обозначим через S _c множество всех синусоидальных сигналов:

S _с = { x: x (t) = S cos | (w t + j)};
– ¥ < t < ¥; S,w Î R⁺, j Î [0, 2p]}. (1)

Здесь R⁺ – множество всех положительных действительных чисел; S на­зывается амплитудой, w – круговой частотой (w = 2p¦, ¦ – частота), j – фазой гармонического колебания.

Модулированные сигналы. В технических системах полезная информация может переноситься каким-нибудь одним параметром “гармонического” колебания. Конечно, колебание при изменении этого параметра во времени перестает быть гармоническим. Процесс изменения параметра синусоиды называется модуляцией, а выделение этого изменения в чистом виде, как бы “снятия” модуляции, называется демодуляцией. Само колебание называется несущим. Различают амплитудную, частотную и фазовую модуляцию в зависимости от того, на какой из параметров несущего колебания “накладывают” полезную информацию (параметры с индексом 0 считаются постоянными):

S _ам = { x: x (t) = S (t) cos (w₀ t + j₀)}, (2)
S _чм = { x: x (t) = S ₀ cos (w(t)· t + j₀)}, (3)
S _фм = { x: x (t) = S ₀ cos (w₀ t + j(t))}. (4)

Необходимо отметить, что “физический смысл” модуляции сохраняется лишь в том случае, когда модулирующий сигнал является “медленно меняющимся” по сравнению с немодулированным несущим колебанием: только при этом условии имеется возможность нестрого, “по-инженерному”, но все-таки не без смысла говорить о “синусоиде с переменной амплитудой (фазой, частотой) “. Однако удобнее все-таки говорить не о “переменной амплитуде”, а об “огибающей”, как это принято в радиотехнике.

Периодические сигналы. Сигналы называются периодическими, а временной интервал t – периодом, если

S _t = { x: x (t) = x (t +t); – ¥ < t < ¥}. (5)

Сигналы с ограниченной энергией. О сигналах из множества

S _э = { x: x ²(t) dt £ K < ¥} (6)

говорят, что их энергия ограничена величиной К. Происхождение этого наз­вания связано с тем, что если х (t) есть напряжение, то интеграл в фор­муле (6) представляет собой энергию, выделенную сигналом х (t) на еди­ничном сопротивлении. Конечно, если х (t) есть, например, глубина бо­роздки на грампластинке, то интеграл связан с энергией лишь косвенно.

Сигналы ограниченной длительности. Интервал Т называется длительностью сигнала х (t), если

S_T = { x: x (t) º 0, t Ï T }; (7)

конечно, предполагается, что внутри этого интервала х (t) не везде обращается в нуль.

Особую роль среди сигналов с ограниченной длительностью играют импульсные сигналы, их отличие состоит в “кратковременности” Т, которую трудно формализовать, но которая проявляется в практике: звуки типа “щелчок”, “взрыв”, “хлопок”; световые “вспышки”; тактильные сигналы “укол”, “щипок”, “удар” и т.п. В таких случаях х (t) обычно называется “формой импульса”. На практике очень распростра­нены периодические последовательности импульсов (радио­ло­ка­ция, элек­трокардиография, ультразвуковая гидролокация и т.п.); не менее важны непериодические импульсные последовательности (те­ле­гра­фия, цифровая телеметрия); в реальности все импульсные последовательности, в свою очередь, имеют ограниченную длительность.

Сигналы с ограниченной полосой частот. Фурье-преобразование Х (¦) временной реализации х (t) сигнала называется ее спектром:

Х (¦) = x (t)e ^{i 2p¦ t} dt. (8)

Физический смысл спектра состоит в том, что колебание х (t) представляется в виде суммы (в общем случае в виде интеграла) составляющих его гармонических колебаний с определенными амплитудами | х (¦)|, частотами ¦ и соответствующими фазами. Между х (t) и Х (¦) имеется взаимно однозначное соответствие, так как

x (t) = X (¦)e^{– i 2p¦ t} dt. (9)

Условием существования и обратимости Фурье-преобразования является ограниченность энергии сигнала (интегрируемость в квадрате функций х (t) и Х (¦)) и его непрерывность.

Если функция Х (¦) на оси ¦ имеет ограниченную “длительность” F (в смысле соотношения (7), но в частотной области), то говорят, что сигнал х (t) имеeт ограниченную полосу частот шириной F:

S_B = { x: Х (¦) = x (t) e ^{i 2p¦ t} dt = 0 для всех ¦ > | F |}. (10)

НЕКОТОРЫЕ МОДЕЛИ АНСАМБЛЯ РЕАЛИЗАЦИЙ

Нормальный шум. Удобной моделью помех и некоторых полезных сигналов является стационарный нормальный случайный процесс. Такое название вызвано тем, что случайные мгновенные значения величины х (t) предполагаются подчиненными нормальному закону (с нулевым средним), т.е. плотность распределения первого порядка выражается формулой

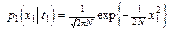; (11)

для плотности распределения второго порядка справедлива формула

(12)

а для n -мерной плотности – формула

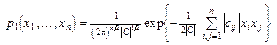. (13)

Использованные здесь обозначения таковы:

N = Е (Х ²) – мощность шума (дисперсия мгновенных значений);

r(t) = N ^-1 Е (Х_t Х_{t +t}) – нормированная функция автокорреляции;

с_ij = Е (Х_tiХ_tj), с_ii = N – коэффициенты ковариации; С = || с_ij ||,
| С | – определитель матрицы С;

| с_ij | – алгебраическое дополнение элемента с_ij, т.е. умноженный на
(– 1) ^{i + j} определитель матрицы (n – 1) -го порядка, полученной из С вычеркиванием i -й строки и j -го столбца.

Замечательной особенностью нормального процесса является то, что его распределение любого порядка полностью определяется только первыми двумя моментными функциями: средним (которое в формулах (11) – (13) принято равным нулю) и ковариационной функцией 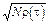, так как с_ij = N r (t_i – t_j).

Сигнал как колебание со случайными огибающей и фазой. Понятия амплитуды и фазы, введенные первоначально для гармонических сигналов, с помощью модуляции были обобщены на сигналы, которые уже не являются гармоническими. Легко обобщить их на произвольные сигналы: пока чисто формально можно задать такие функции R (t) и j(t), чтобы для заданной функции х (t) было выполнено равенство

Bandpass полоса частот REALIZATION реализация NARROW-BAND узкополосный     Установив, что случайный процесс является приемлемой моделью сигналов, мы должны построить конкретные варианты этой модели – как на уровне описания отдельных реализаций, так и с помощью моделирования сразу всего ансамбля возможных реализаций. Современная теория сигналов предлагает модели обоих типов.

x (t)= R (t)cos(?₀ t +?(t)), (14)

и, сравнив его с соотношениями (1) – (4), можно трактовать R (t) и j(t) как “огибающую” и “фазу” колебания с частотой w₀.

Возникает вопрос: соответствуют ли эти функции чему-нибудь реальному? Оказывается, свобода выбора в задании функций R и j при определенных условиях весьма ограничена. Эти условия мы уже упоминали как “медленность” R (t) по сравнению с cosw₀ t и j(t) по сравнению с w₀ t, а в целом этот комплекс условий в силу причин (которые мы не будем обсуждать) получил название узкополосности сигнала х (t).

Очень наглядным является векторный вариант модели (14): R и j можно рассматривать как полярные координаты некоторого вектора. Тогда всякое гармоническое колебание х (t) = S cos(w₀ t + j), имеющее частоту w₀, изобразится как постоянный вектор с амплитудой S и углом j к направлению, принятому за ось 0 х.

Если гармонический сигнал имеет частоту, отличную от w₀ (например, w₁), то в рассматриваемой системе координат соответствующий ему вектор будет вращаться с частотой
w₁ –... w₀, поскольку соsw₁ t = соs(w₀ t + j(t)),
j(t) = (w₁ – w₀) t. Негармонический сигнал изобразится как вектор, совершающий вращения или колебания (изменяется угол) и изменяющий свою длину R.

При всей простоте такая модель позволяет легко описывать различные преобразования сигналов. Например, сумма двух колебаний с частотой w₀ изобразится как сумма двух соответствующих векторов (при этом автоматически учитываются фазовые соотношения).

Пусть, например, принимаемый сигнал является суммой полезного сигнала s (t) и шума n (t):

х (t) = s (t) + n (t). (15)

Рассмотрим случай, когда полезный сигнал есть гармоническое колебание

s (t) = S · cosw₀ t, (16)

а шум является нормальным с дисперсией s²и нулевым средним. Будем считать, что w₀ значительно превышает ширину полосы частот, занимаемую сигналом х (t), так что такая узкополосность обеспечивает физический смысл понятиям его огибающей и фазы (см. формулу (14)). Направив ось 0 х вдоль вектора сигнала s (t), находим его координаты х = S и y = 0. Вектор шума случаен, обе его компоненты нормальны с нулевым средним и дисперсией s². Сложение векторов сигнала и шума приводит к вектору с нормальными компонентами, у одной из которых среднее равно S, а у другой – нулю:

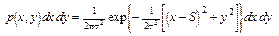. (17)

Поскольку существуют радиотехнические устройства, чувствительные только к огибающей или только к фазе принимаемого сигнала, имеет смысл рассмотреть их статистические свойства. Перейдем от декартовых координат (х, у) к полярным (R, j). Используя очевидные соотношения х = R соsj, y = R sinj, dх dy = R dR d j, из равенства (17) сразу получаем распределение

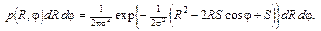(18)

Легко установить, что если S = 0 (т.е. имеется только чистый шум), то

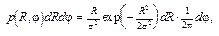(19)

т.е. огибающая распределена по закону Рэлея, фаза – равномерно в интервале [0, 2??, R и? независимы (так как их совместное распределение факторизовалось).

Распределения вероятностей отдельно для огибающей R и фазы? получаются при интегрировании совместного распределения (18) по переменной, которую нужно исключить. Например, распределение огибающей имеет вид

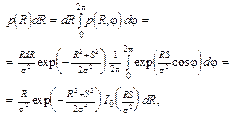(20)

5.2 ————— График плотностей распределения вероятностей для фазы колебания, являющегося аддитивной смесью смеси синусоидального сигнала с шумом

5.1
—————
График плотностей распределения вероятностей огибающей
смеси синусоидального сигнала с гауссовым шумом

 

где через I ₀ обозначена модифицированная функция Бесселя первого рода нулевого порядка (так называется трансцендентная функция, выражаемая полученным интегралом). Это распределение называется распределением Рэля–Райса или обобщенным распределением Рэлея, поскольку при S = 0 оно обращается в обычное распределение Рэлея. Семейство кривых р (R) для различных S и? изображено на рис. 5.1.

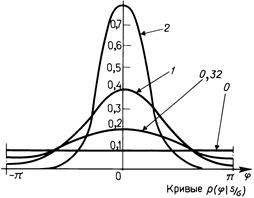
Распределение фазы выражается формулой

p (?) d? = d? p (R,?) dR. (21)

Не приводя аналитических выражений для р (?) из-за их громоздкости (при необходимости см. [5]), изобразим графики этого распределения при разных S /? на рис. 5.2.

 

Подведем итог В данном параграфе приведено несколько наиболее употребительных моделей сигналов. Следует помнить, что в ряде случаев эти модели достаточно хорошо отображают реальные сигналы, но абсолютно точными они не бывают никогда.

Summary Several widely used models of signals have been presented in this section. It is necessary to remember that in many cases these models represent real signals well enough, but that they are never absolutely exact.

⇐ Предыдущая891011121314151617Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: