О некоторых свойствах непрерывных сигналов

Хотя мы излагаем лишь элементы теории сигналов, преследуя только ознакомительные цели, представляется интересным рассмотреть два основных ее аспекта, относящихся к свойствам непрерывных сигналов.

ЧАСТОТНО-ВРЕМЕННОЕ ПРЕДСТАВЛЕНИЕ СИГНАЛОВ

Первый – это частотно-временная неопределенность сигналов.

Известно, что некоторая функция х (t) и ее спектр Х (¦) однозначно выражаются друг через друга (см. формулы (8) и (9) § 5.4). Следовательно, сигнал можно рассматривать в любом из этих эквивалентных представлений – временном или частотном. При этом масштабные параметры этих представлений связаны обратно пропорциональной зависимостью. Пусть х (t) имеет спектр Х (¦). Изменим масштаб по оси времени в а раз (например, воспроизведем запись х (t) с другой скоростью) и найдем спектр функции х (аt):

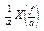Х_a (¦) = х (аt)е ^{i 2?¦ t} dt = . (1)

Как видим, масштаб по частотной оси изменился в 1/ а раз. Более того, из свойств преобразования Фурье следует, что сигналы с ограниченной длительностью имеют спектры неограниченной ширины, а сигналы с ограниченной полосой частот длятся бесконечно долго.

Этот математический результат находится в противоречии с практикой: в реальности все сигналы конечны по длительности, а все чувствительные к сигналам устройства не могут воспринимать и воспроизводить абсолютно все частоты. Например, диапазон частот, к которым чувствителен слух человека, простирается от нескольких герц до 20 – 30 кГц, а все различимые звуки человеческой речи длятся доли секунды.

Тот факт, что аналитическая функция времени не может быть одновременно ограниченной и по длительности, и по ширине спектра, является, как видим, не свойством реальных сигналов, а свойством данной модели сигналов. В § 5.3 мы уже отмечали, что если не отказываться от достоинств аппарата аналитических функций, то выход состоит в том, чтобы как-то иначе ввести в рассмотрение конечную точность реализаций функций времени. Правда, пока эта конечная точность не будет свойством самих реализаций, ее искусственное введение в модель можно проводить на разных этапах, что придает результатам некоторую относительность.

Например, говорить об одновременной ограниченности сигналов и по времени, и по спектру оказывается возможным при использовании энергетического критерия точности: сигнал считается имеющим конечную длительность? Т, если в этом интервале времени сосредоточена основная часть всей энергии функции х (t); в то же время и ширина спектра? F сигнала определяется как область частот, содержащая эту же часть всей энергии спектра Х (¦):

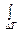x ²(t) dt = X ²(¦) d ¦ =? 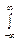x ²(t) dt =? 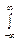X ²(¦) d ¦, (2)

Здесь величина? меньше единицы, но достаточно близка к ней, а величина 1 –? характеризует косвенным образом точность, о которой шла речь.

Теперь можно говорить о том, какую “площадь” на плоскости “частота – время” занимает тот или иной сигнал. Если строго следовать теории Фурье-преобразований, то получим, что эта площадь для всех сигналов бесконечна, но для большинства из них энергетический критерий позволит ограничить ее естественным образом (рис. 5.3). Меняя форму сигнала s (t), можно менять и занимаемую им площадь. Оказывается [4], что уменьшать эту площадь можно лишь до некоторого предела. Этот предел достигается на кривой, являющейся гармоническим колебанием, которое модулировано по амплитуде гауссовым импульсом; интересно, что спектр этой кривой имеет такую же форму:

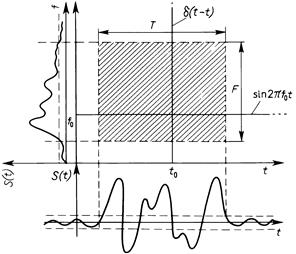5.3 ————— Иллюстрация частотно-временной неопределенности сигнала

UNCERTAINTY неопределенность CONTINUOUS непрерывный LIMIT предел FREQUENCY частота     Все реальные сигналы длятся конечное время, и все реальные системы не могут реагировать на абсолютно все частоты. Следовательно, как длительность, тек и ширина спектра сигнала ограничены. Аналитическая модель сигнала позволяет говорить об этих характеристиках приближенно. В этом мы видим конкретный пример проявления расхождений между моделью и оригиналом. Практически всякий сигнал можно представить состоящим из более простых компонент. В математике этой идее соответствует представление функций их разложениями в ряды и интегралы. В теории сигналов специальное внимание уделяется условиям, при которых непрерывные функции можно однозначно представить в виде дискретного набора элементарных функций.

(3)
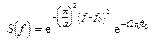. (4)

Существование предела, ниже которого нельзя сжать площадь сигнала, занимаемую им на плоскости “частота – время”, и называется (по аналогии с принципом неопределенности в квантовой механике) принципом частотно-временной неопределенности сигналов:

? F ·? T ³?const > 0. (5)

ДИСКРЕТНОЕ ПРЕДСТАВЛЕНИЕ СИГНАЛОВ

Вторым важным аспектом теории сигналов является проблема дискрет­ного представления непрерывных сигналов. Вопрос формулируется так: существуют ли условия (и если да, то каковы они), при которых любой непрерывной функции х (t) можно поставить во взаимно однозначное со­ответствие дискретное множество чисел { С_k (х)}, k =... – 2, – 1, 0, 1, 2,...? Положительный ответ на этот вопрос имел бы как теоретическое, так и практическое значение. Во-первых, рассмотрение случайных величин вместо реализаций непрерывных случайных процессов существенно упрощает решение многих задач, вся теория становится проще и может быть продвинута дальше. Во-вторых, соответствие х (t) «{ С_k (х)} можно использовать и в технических устройствах, работающих с непрерывными сигналами (например, иногда технически проще хранить или передавать { С_k (х)} вместо х (t)).

Ограничимся более конкретной формулировкой поставленной задачи и рассмотрим ус­ло­вия выполнения равенства

x (t) = 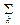C_k (x)? _k (t). (6)

Функции {? _k (t) } называются координатными функ­циями, они не должны зависеть от х (t), более того, они заранее известны. Ряд в правой час­ти равенства называется разложением х (t) по координатным функциям. Числовые коэффициен­ты { С_k (х)} содержат всю информацию об х (t), необходимую для восстановления этой функции по формуле (6); следовательно, { С_k (х)} являются функционалами* от функции х (t).

—————————— * Функционалом называется отображение множества функций в множество чисел.

Наиболее известны разложения по системе ортогональных и норми­ро­ванных функций. Это означает, что функции {? _k (t)} удов­лет­во­ря­ют ус­ловиям

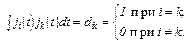(7)

Умножим обе части равенства (6) на? _i (t) и проинтегрируем (опуская тонкости, будем считать, что все операции обоснованы):

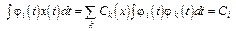. (8)

Такое представление называют рядом Фурье, а С_k (х) – ко­эф­фи­ци­ен­тами Фурье. Условия сходимости ряда Фурье к функции х (t) подробно исследованы и, кратко говоря, сводятся к тому, чтобы были оправданы все необходимые математические операции, а коэффициенты Фурье убывали достаточно быстро (точнее, 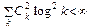). Это не очень жест­кое ограничение, но все же оно связывает свойства системы координатных функций и самих функций х (t). Например, если {? _k (t) } – гар­мо­ни­чес­кие функции кратных частот, то х (t) должна быть периодической функцией с периодом Т, равным периоду самой низкочастотной гармоники:

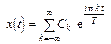, (9)
. (10)

Значительный интерес привлекли разложения реализаций случайного процесса с ограниченной полосой частот. Для таких сигналов В.А. Котельников доказал (1946) следующую теорему (теорему отсчетов):

любая функция со спектром, находящимся в интервале [0, F ], полностью определяется последовательностью ее значений в точках, отстоящих друг от друга на 1/ (2 F) единиц времени.

Пусть х (t) имеет спектр Х (¦); эти функции связаны соотношениями (8) и (9) § 5.4, причем Х (¦) отлично от нуля только в интервале |¦| £ F.

В этом интервале применимо разложение (9):

,

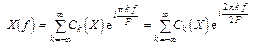а коэффициенты Фурье этого разложения таковы:

.

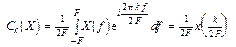Следовательно,

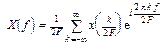, (11)

и это соотношение уже доказывает теорему отсчетов в силу однозначной связи Х (¦) с х (t).

Чтобы показать в явном виде, как восстанавливать х (t) для значений t между точками отсчетов, воспользуемся формулой (9) § 5.4:

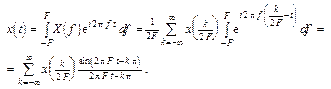(12)

Итак, мы получили разложение реализации, координатными функциями которого являются функции вида (sin u) / u, сдвинутые друг относительно друга на интервалы времени 1/(2 F), а коэффициентами – зна­чения (“отсчеты”) самой реализации, взятые в моменты k / (2 F).

Иногда говорят, что эта теорема является теоретическим обоснованием возможности на практике восстанавливать х (t) по отсчетам 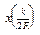. Однако дело в том, что координатные функции имеют неограниченную длительность и, следовательно, физически нереализуемы. Кроме того, ряд (12) имеет неограниченное число членов. Все это снова возвращает нас к проблеме точности фиксации сигналов, – проблеме, пока не получившей полного освещения*.

 

Подведем итог Из многочисленных результатов теории сиг­налов мы выделяем два, как существен­но поясняющие природу непрерывных сиг­налов. Первый состоит в том, что сигналы обнаруживают своеобразную “упругость” за­нимаемой ими площади на плоскости “час­тота-время”. Это явление называется час­тотно-временной неопределенностью сиг­налов. Второй результат заключается в том, что определенный класс непрерывных сигналов допускает взаимно однозначное соответствие между любой реализацией из этого класса и дискретным набором отсчетов данной реализации.

Summary From the numerous results of signal theory we single out two that substantially clarify the nature of continuous signals. The first is that the simultaneous time-and-frequency representation of signals exposes a sort of “elasticity” of an area occupied by a signal on a time-frequency plane. This phenomenon is called the time-and-frequency uncertainty of signals. The second result is that a certain class of continuous signals allows a one-to-one correspondence between any function from this class and a set of the values of this function at discrete moments in time.

ЭНТРОПИЯ

Установив, что случайные процессы являются адекватной моделью сигналов (см. § 5.3), мы получаем возможность воспользоваться результатами и мощным аппаратом теории случайных процессов. Кроме того, обнаружив, что некоторые типы непрерывных сигналов допускают дискретное представление (см. § 5.5), мы упрощаем задачу, сводя все к рассмотрению случайных величин.

Это не означает, что теория вероятностей и теория случайных процессов дают готовые ответы на все вопросы о сигналах: подход с новых позиций выдвигает такие вопросы, которые раньше просто не возникали. Так и родилась теория информации [9], специально рассматривающая сигнальную специфику случайных процессов. При этом были построены принципиально новые понятия (которые мы рассмотрим в данном и следующем параграфах) и получены новые, неожиданные результаты, имеющие характер научных открытий (наиболее важные из них мы обсудим в § 5.8).

ПОНЯТИЕ НЕОПРЕДЕЛЕННОСТИ

Первым специфическим понятием теории информации является понятие неопределенности случайного объекта, для которой удалось ввести количественную меру, названную энтропией. Начнем с простейшего варианта – со случайного события. Пусть, например, некоторое событие может произойти с вероятностью 0,99 и не произойти с вероятностью 0,01, а другое событие имеет вероятности соответственно 0,5 и 0,5. Очевидно, что в первом случае результатом опыта “почти наверняка” является наступление события, во втором же случае неопределенность исхода так велика, что от прогноза разумнее воздержаться.

Для характеристики размытости распределений широко используется второй центральный момент (дисперсия) или доверительный интервал. Однако эти величины имеют смысл лишь для случайных числовых величин и не могут применяться к случайным объектам, состояния которых различаются качественно, хотя и в этом случае можно говорить о большей или меньшей неопределенности исхода опыта. Следовательно, мера неопределенности, связанная с распределением, должна быть некоторой его числовой характеристикой, функционалом от распределения, никак не связанным с тем, в какой шкале измеряются реализации случайного объекта.

ЭНТРОПИЯ И ЕЕ СВОЙСТВА

Примем (пока без обоснования) в качестве меры неопределенности случайного объекта А с конечным множеством возможных состояний
А ₁,..., А _n с соответствующими вероятностями p ₁,..., р _n величину

, (1)

которую и называют энтропией случайного объекта А (или распределения { р_i }). Убедимся, что этот функционал обладает свойствами, которые вполне естественны для меры неопределенности.

1⁰. Н (р ₁,..., р_n) = 0 в том и только в том случае, когда какое-нибудь од­но из { р_i } равно единице (а остальные – нули). Это соответствует случаю, когда исход опыта может быть предсказан с полной достоверностью, т.е. когда отсутствует всякая неопределенность. Во всех других слу­чаях энтропия положительна. Это свойство проверяется непосредственно.

2⁰. Н (р ₁,..., р_n) достигает наибольшего значения при р ₁ = р ₂ = =... = р_n = 1/ n, т.е. в случае максимальной неопределенности.

Действительно, вариация Н по р_i при условии S р_i = 1 дает р_i = = const = .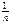

3⁰. Если А и В – независимые случайные объекты, то

Н (А Ç В) = Н ({? _ik = р_iq_k }) = Н ({ р_i }) + Н ({ q_k }) = Н (А) + Н (В).

Это свойство проверяется непосредственно.

4⁰. Если А и В – зависимые случайные объекты, то

Н (А Ç В) = Н (А) + Н (В | А) = Н (В) + Н (А | В), (2)

где условная энтропия Н (В | А) определяется как математическое ожидание энтропии условного распределения.

Это свойство проверяется непосредственно.

5⁰. Имеет место неравенство Н (А) ³ Н (А | В), что согласуется с интуитивным представлением о том, что знание состояния объекта В может только уменьшить неопределенность объекта А, а если они независимы, то оставит ее неизменной.

Это свойство доказывается с помощью тождественного неравенства

,

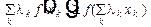справедливого для любой выпуклой функции f (х), если в этом неравенстве положить f (х) = х log х,? _k = р_k, х_k = q_{k | l} .

Как видим, свойства функционала Н позволяют использовать его в качестве меры неопределенности. Интересно отметить, что если пойти в обратном направлении, т.е. задать желаемые свойства меры неопределен­ности и искать обладающий указанными свойствами функционал, то уже только условия 2⁰ и 4⁰ позволяют найти этот функционал, и при­том единственнымобразом (с точностью до постоянного множителя).

ДифференциальнаЯ ЭНТРОПИЯ

Обобщение столь полезной меры неопределенности на непрерывные случайные величины наталкивается на ряд сложностей. Можно по-разному преодолеть эти сложности; выберем кратчайший путь. Прямая аналогия

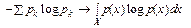
не приводит к нужному результату; плотность р (х) является размерной величиной*, а логарифм размерной величины не имеет смысла. Однако положение можно исправить, умножив р (х) под знаком логарифма на величину E, имеющую ту же размерность, что и х:

.

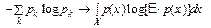Теперь величину E можно принять равной единице измерения х, что приводит к функционалу

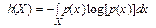, (3)

который получил название дифференциальной энтропии. Это аналог энтропии дискретной величины, но аналог условный, относительный: ведь единица измерения произвольна. (Здесь [ p (x)] есть безразмерное представление плотности.) Запись (3) означает, что мы как бы сравниваем неопределенность случайной величины, имеющей плотность р (х), с неопределенностью случайной величины, равномерно распределенной в единичном интервале. Поэтому величина h (Х) в отличие от Н (Х) может быть не только положительной. Кроме того, h (Х) изменяется при нелинейных преобразованиях шкалы х, что в дискретном случае не играет роли. Остальные свойства h (Х) аналогичны свойствам Н (Х), что делает дифференциальную энтропию очень полезной мерой.

Пусть, например, задача состоит в том, чтобы, зная лишь некоторые ограничения на случайную величину (типа моментов, пределов сверху и снизу области возможных значений и т.п.), задать для дальнейшего (ка­ких-то расчетов или моделирования) конкретное распределение. Одним из подходов к решению этой задачи дает принцип максимума энтропии: из всех распределений, отвечающих данным ограничениям, следует выбирать то, которое обладает максимальной дифференциальной энтропией. Смысл этого критерия состоит в том, что, выбирая экстремальное по энтропии распределение, мы гарантируем наибольшую неопределенность, связанную с ним, т.е. имеем дело с наихудшим случаем при данных условиях.

ФУНДАМЕНТАЛЬНОЕ СВОЙСТВО ЭНТРОПИИ СЛУЧАЙНОГО ПРОЦЕССА

Особое значение энтропия приобретает в связи с тем, что она связана с очень глубокими, фундаментальными свойствами случайных процессов. Покажем это на примере процесса с дискретным временем и дискретным конечным множеством возможных состояний.

PROBABILITY вероятность INDEPENDENT независимый SYMBOL символ ENTROPY энтропия ERGODICITY эргодичность     Важным шагом в постро­ении теории информации является введение количественной меры неопределенности – эн­тро­пии. Оказывается, что функционал (1) обладает качествами, которые логично ожидать от меры неопределенности, и, наоборот, единственным функционалом с такими свой­ствами является именно функционал энтропии. Обобщение понятия энтропии на непрерывные случайные величины приводит к выводу, что такое обобщение – дифференци­альная энтропия – воз­можно лишь как относительная мера. Оказывается, что энтропия связана с глубокими свойствами случайных процессов. Например, для дискретных процессов имеет место свойство асимптотической равновероятности реализаций из высоковероятной группы.

Назовем каждое такое состояние символом, множество возможных состояний – алфавитом, их число m – объемом алфавита. Число всевозможных последовательностей длины n, оче­вид­но, равно mⁿ. Появление конкретной последовательности можно рассматривать как реализацию одного из mⁿ возможных событий. Зная вероятности символов и условные вероятности появления следующего символа, если известен пре­ды­дущий (в случае их зависимости), можно вы­чис­лить вероятность Р (С) для каждой последовательности С. Тогда энтропия множества { С }, по определению, равна

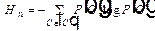. (4)

—————————— * Существование такого предела для любого стационарного процесса можно строго доказать.

Определим энтропию процесса Н (среднюю неопределенность, приходящуюся на один символ) следующим образом*:

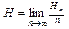. (5)

На множестве { С } можно задать любую числовую функцию f_n (С), которая, очевидно, является случайной величиной. Определим f_n (С) с помощью соотношения

.

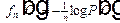Математическое ожидание этой функции

,

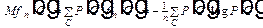откуда следует, что

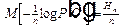, и
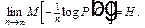(6)

Это соотношение, весьма интересное уже само по себе, является, однако, лишь одним из проявлений гораздо более общего свойства дискретных эргодических процессов. Оказывается, что не только математическое ожидание величины f_n (С) при n ®¥ имеет своим пределом Н, но сама эта величина f_n (С) стремится к Н при n ®¥. Другими словами, как бы малы ни были Е > 0 и? > 0, при достаточно большом n справедливо неравенство [9]

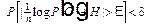, (7)

т.е. близость f_n (С) к Н при больших n является почти достоверным событием.

Для большей наглядности сформулированное фундаментальное свойство случайных процессов обычно излагают следующим образом. Для любых заданных E > 0 и??> 0 можно найти такое n ₀, что реализации любой длины n > n ₀ распадаются на два класса:

группа реализаций, вероятности Р (С) которых удовлетворяют неравенству

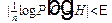; (8)

группа реализаций, вероятности которых этому неравенству не удовлетворяют.

Так как согласно неравенству (7) суммарные вероятности этих групп равны соответственно 1 –? и?, то первая группа называется высоковероятной, а вторая – маловероятной.

Это свойство эргодических процессов приводит к ряду важных следствий, из которых три заслуживают особого внимания.

1⁰. Независимо от того, каковы вероятности символов и каковы статистические связи между ними, все реализации высоковероятной группы приблизительно равновероятны (см. формулу (8)).

В связи с этим фундаментальное свойство иногда называют “свой­ством асимптотической равнораспределенности”. Это следствие, в част­ности, означает, что по известной вероятности Р (С) одной из реализаций высоковероятной группы можно оценить число N ₁ реализаций в этой группе:

.

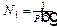2⁰. Энтропия Н_n с высокой точностью равна логарифму числа реализации в высоковероятной группе:

Н_n = nН = log N ₁. (9)

3⁰. При больших n высоковероятная группа обычно охватывает лишь ничтожную долю всех возможных реализаций (за исключением случая равновероятных и независимых символов, когда все реализации равновероятны и Н = log m).

Действительно, из соотношения (9) имеем N ₁ = а^nH, где а – основание логарифма. Число N всех возможных реализаций есть N = mⁿ = а^{n log m} . Доля реализаций высоковероятной группы в общем числе реализаций выражается формулой

N ₁/ N = a ^{– n (log m – Н)}, (10)

и при Н < log m эта доля неограниченно убывает с ростом n. Например, если a = 2, n = 100, Н =2,75, m = 8, то N ₁/ N = 2^–25 ~ = (3·10⁷)^-1, т.е. к высоковероятной группе относится лишь одна тридцатимиллионная доля всех реализаций!

Строгое доказательство фундаментального свойства эргодических процессов сложно и здесь не приводится. Однако следует отметить, что в простейшем случае независимости символов это свойство является следствием закона больших чисел. Действительно, закон больших чисел утверждает, что с вероятностью, близкой к 1, в длинной реализации i -й символ, имеющий вероятность р_i, встретится примерно nр_i раз. 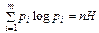Следовательно, вероятность реализации высоковероятной группы есть , откуда – log Р (С) = – n , что и доказывает справедливость фундаментального свойства в этом случае.

 

Подведем итог Связав понятие неопределенности дискретной величины с распределением вероятности по возможным состояниям и потребовав некоторых естественных свойств от количественной меры неопределенности, мы приходим к выводу, что такой мерой может служить только функционал (1), названный энтропией. С некоторыми трудностями энтропийный подход удалось обобщить на непрерывные случайные ве­ли­чи­ны (введением дифференциальной энтропии (3)) и на дискретные случайные процессы.

Summary Linking the concept of the uncertainty of a discrete random variable and the form of its probability distribution, and demanding certain reasonable properties from the quantitative measure of uncertainty, we arrive at the conclusion that such a measure may only be the functional (1), which is called entropy. The entropy approach may be extended (with some difficulty) to continuous random variables – by the introduction of differential entropy (3) – as well as to random processes (we have considered here only discrete processes).

КОЛИЧЕСТВО ИНФОРМАЦИИ

В основе всей теории информации лежит открытие, что информация допускает количественную оценку. В простейшей форме эта идея была выдвинута еще в 1928 г. Хартли, но завершенный и общий вид придал ей Шэннон в 1948 г. [9]. Не останавливаясь на том, как развивалось и обобщалось понятие количества информации, дадим сразу его современное толкование.

КОЛИЧЕСТВО ИНФОРМАЦИИ
КАК МЕРА СНЯТОЙ НЕОПРЕДЕЛЕННОСТИ

Процесс получения информации можно интерпретировать как изменение неопределенности в результате приема сигнала. Проиллюстрируем эту идею на примере достаточно простого случая, когда передача сигнала происходит при следующих условиях: 1) полезный (от­прав­ля­е­мый) сигнал является последовательностью статистически не­за­ви­си­мых символов с вероятностями р (х_i), 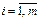; 2) принимаемый сигнал является последовательностью символов у_k того же алфавита; 3) если шумы (ис­ка­жения) отсутствуют, то принимаемый сигнал совпадает с отправляемым у_k = х_i; 4) если шум имеется, то его действие приводит к тому, что данный символ может либо остаться прежним (i -м), либо быть подмененным любым другим (k -м) символом, вероятность этого равна р (у_k | х_i); 5) искажение очередного символа является событием, статистически независимым от того, что произошло с предыдущими символами. Конечно, можно рассматривать ситуацию и со стороны передатчика, используя вероятности р (х_i | у_k) (рис. 5.4). В этих условиях энтропия процесса есть энтропия одного символа, и все сводится к рассмотрению посимвольного приема.

Итак, до получения очередного символа ситуация характеризуется неопределенностью того, какой символ будет отправлен, т.е. априорной энтропией Н (Х). После получения символа у_k неопределенность относительно того, какой символ был отправлен, меняется: в случае отсутствия шума она вообще исчезает (апостериорная энтропия равна нулю, поскольку точно известно, что был передан символ х_k = у_k), а при наличии шума мы не можем быть уверены, что полученный нами символ и есть отправленный, и возникает неопределенность, характеризуемая апостериорной энтропией Н (Х | у_k) = Н ({ р (х_i | у_k)}) > 0. В среднем после получения очередного символа энтропия Н (Х | Y) = M_yН (Х | у_k).

Определим теперь количество информации как меру снятой неопределенности: числовое значение количества информации о некотором объекте равно разности априорной и апостериорной энтропий этого объекта, т.е.

I (Х, Y) = Н (Х) – Н (X | Y). (1)

Использовав равенство (2) § 5.6, легко получить, что

I (Х, Y) = Н (Y) – Н (Y | Х). (2)

В явной форме равенство (1) запишется так:

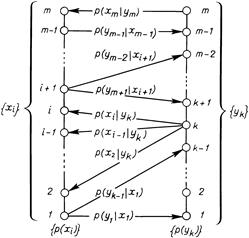5.4 ————— Схема “вееров неопределенности” при наличии шума в канале

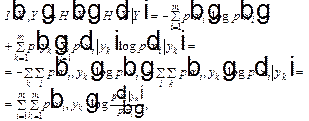(3)

а для равенства (2) имеем

(4)

КОЛИЧЕСТВО ИНФОРМАЦИИ
КАК МЕРА СООТВЕТСТВИЯ
СЛУЧАЙНЫХ ОБЪЕКТОВ

 

Этим формулам легко придать полную симметричность: умножив и разделив логарифмируемое выражение в (3) на р (у_k), а в (4) на р (х_i), сразу получим, что

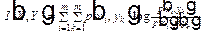(5)

Эту симметрию можно интерпретировать так: количество информации в объекте Х об объекте Y равно количеству информации в объекте Y об объекте Х. Таким образом, количество информации является не характеристикой одного из объектов, а характеристикой их связи, соответствия между их состояниями. Подчеркивая это, можно сформулировать еще одно определение: среднее количество информации, вычисляемое по формуле (5), есть мера соответствия двух случайных объектов.

Это определение позволяет прояснить связь понятий информации и количества информации. Информация есть отражение одного объекта другим, проявляющееся в соответствии их состояний. Один объект может быть отражен с помощью нескольких других, часто какими-то лучше, чем остальными. Среднее количество информации и есть числовая характеристика степени отражения, степени соответствия. Подчеркнем, что при таком описании как отражаемый, так и отражающий объекты выступают совершенно равноправно. С одной стороны, это подчеркивает обоюдность отражения: каждый из них содержит информацию друг о друге. Это представляется естественным, поскольку отражение есть результат взаимодействия, т.е. взаимного, обоюдного изменения состояний. С другой стороны, фактически одно явление (или объект) всегда выступает как причина, другой – как следствие; это никак не учитывается при введенном количественном описании информации.

Формула (5) обобщается на непрерывные случайные величины, если в соотношения (1) и (2) вместо Н подставить дифференциальную энтропию h; при этом исчезает зависимость от стандарта Е и, значит, количество информации в непрерывном случае является столь же безотносительным к единицам измерения, как и в дискретном:

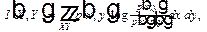(6)

где р (х), р (y) и р (х, y) – соответствующие плотности вероятностей.

Свойства КОЛИЧЕСТВА ИНФОРМАЦИИ

Отметим некоторые важные свойства количества информации.

1⁰. Количество информации в случайном объекте Х относительно объекта Y равно количеству информации в Y относительно Х:

I (Х, Y) = I (Y, Х). (7)

2⁰. Количество информации неотрицательно:

I (Х, Y) ³ 0. (8)

Это можно доказать по-разному. Например, варьированием р (х, y) при фиксированных р (х) и р (y) можно показать, что минимум I, равный нулю, достигается при р (х, у) = p (х) p (y).

3⁰. Для дискретных Х справедливо равенство

I (Х, Х) = Н (Х).

4⁰. Преобразование?(·) одной случайной величины не может увеличить содержание в ней информации о другой, связанной с ней, величине:

I (? (Х), Y) £ I (Х, Y) (9)

5⁰. Для независимых пар величин количество информации аддитивно:

I ({ X_i, Y_i }) = 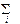I (X_i, Y_i). (10)

INTERACTION взаимодействие DISTORTION искажение QUANTITY количество DENSITY плотность AVERAGE средний   Количество информации можно определить как меру уменьшения неопределенности в результате получения сигнала. Это соответствует разности энтропий до и после приема сигнала. Среди свойств количества информации выделяются следующие: 1) количество информации (в отличие от энтропии) имеет одинаковый смысл как для дискретных, так и для непрерывных случайных объектов; 2) при обработке данных содержащееся в них количество информации не может быть увеличено. Следовательно, обработка делается лишь для представления информации в более удобном, компактном виде и в лучшем случае без потери полезной информации.

ЕДИНИЦЫ ИЗМЕРЕНИЯ ЭНТРОПИИ
И КОЛИЧЕСТВА ИНФОРМАЦИИ

Рассмотрим теперь вопрос о единицах измерения количества информации и энтропии. Из определений I и Н следует их безразмерность, а из линейности их связи – одинаковость их единиц. Поэтому будем для определенности говорить об энтропии. Начнем с дискретного случая. За единицу энтропии примем неопределенность случайного объекта, такого, что

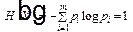. (11)

Легко установить, что для однозначного определения единицы измерения энтропии необходимо конкретизировать число m состояний объекта и основание логарифма. Возьмем для определенности наименьшее число возможных состояний, при котором объект еще остается случайным, т.е. m = 2, и в качестве основания логарифма также возьмем число 2. Тогда из равенства –р₁log₂р₁ – р₂log₂р₂ = 1 вытекает, что р₁ = р₂ = 1/2. Следовательно, единицей неопределенности служит энтропия объекта с двумя равновероятными состояниями. Эта единица получила название “бит”. Бросание монеты дает количество информации в один бит. Другая единица (“нит”) получается, если использовать натуральные логарифмы, обычно она употребляется для непрерывных величин.

КОЛИЧЕСТВО ИНФОРМАЦИИ В ИНДИВИДУАЛЬНЫХ СОБЫТИЯХ

Остановимся еще на одном важном моменте. До сих пор речь шла о среднем количестве информации, приходящемся на любую пару состояний (х _i, у_k) объектов Х и Y. Эта характеристика естественна для рассмотрения особенностей стационарно функционирующих систем, когда в процессе функционирования (рано или поздно, реже или чаще) принимают участие все возможные пары (х_i, у_k). Однако в ряде практических случаев оказывается необходимым рассмотреть информационное описание конкретной пары состояний, оценить содержание информации в конкретной реализации сигнала. Тот факт, что некоторые сигналы несут информации намного больше, чем другие, виден на примере того, как отбираются новости средствами массовой информации (скажем, все радиостанции и газеты сообщают о рождении шестерых близнецов где-то в Южной Америке, но о рождении двойни обычно не пишут).

Допуская существование количественной меры информации i(х_i, у_k) в конкретной паре (х_i, у_k), естественно потребовать, чтобы индивидуальное и среднее количества информации удовлетворяли соотношению

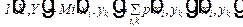. (12)

Хотя равенство сумм имеет место не только при равенстве всех слагаемых, сравнение формул (12) и, например, (4) наталкивает на мысль, что мерой индивидуальной информации в дискретном случае может служить величина

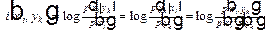, (13)

а в непрерывном – величина

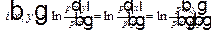, (14)

называемая информационной плотностью. Свойства этих величин согласуются с интуитивными представлениями (в том числе и возможная отрицательность при положительности в среднем) и, кроме того, доказана единственность меры, обладающей указанными свойствами. Полезность введения понятия индивидуального количества информации проиллюстрируем на следующем примере.

Пусть по выборке (т.е. совокупности наблюдений) х = х ₁,..., х_N требуется отдать предпочтение одной из конкурирующих гипотез (Н ₁ или Н ₀), если известны распределения наблюдений при каждой из них, т.е. р (х | Н ₀) и р (х | Н ₁). Как обработать выборку? Из т

⇐ Предыдущая9101112131415161718Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: