Описание выбора на языке бинарных отношений

Второй, более общий язык, на котором описывается выбор, – это язык бинарных отношений. Его большая, нежели у критериального языка, общность основана на учете того факта, что в реальности дать оценку отдельно взятой альтернативе часто затруднительно или невозможно; однако если рассматривать ее не в отдельности, а в паре с другой альтернативой, то находятся основания сказать, какая из них более предпочтительна.

Таким образом, основные предположения этого языка сводятся к следующему:

1) отдельная альтернатива не оценивается, т.е. критериальная функция не вводится;

2) для каждой пары альтернатив (x, y) некоторым образом можно установить, что одна из них предпочтительнее другой либо они равноценны или несравнимы (чаще всего последние два понятия отождествляются);

3) отношение предпочтения внутри любой пары альтернатив не зависит от остальных альтернатив, предъявленных к выбору.

Математически бинарное отношение R на множестве X определяется как определенное подмножество упорядоченных пар (x, y). Удобно использовать обозначение xR у, если x находится в отношении R с y, и x y – в противном случае. Множество всех пар {(x, y), x, y Î X} называется полным (“универсальным”) бинарным отношением. Поскольку в общем случае не все возможные пары (x, y) удовлетворяют условиям, накладываемым отношением R, бинарное отношение является некоторым подмножеством полного бинарного отношения, т.е. R Í X ´ X.

Задать отношение – это значит тем или иным способом указать все пары (x, y), для которых выполнено отношение R.

СПОСОБЫ ЗАДАНИЯ БИНАРНЫХ ОТНОШЕНИЙ

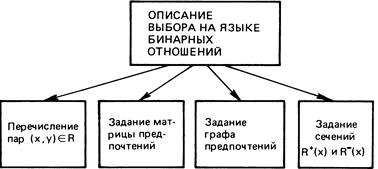7.3 ————— Способы описания выбора на языке бинарных отношений

Существует четыре разных способа задания отношений (рис. 7.3); преимущества каждого проявляются при разных характеристиках множества X.

Первый, очевидный, способ состоит в непосредственном перечислении таких пар. Ясно, что он приемлем лишь в случае конечного множества X.

Второй удобный способ задания отношения R на конечном множестве – матричный. Все элементы нумеруются, и матрица отношения R определяется своими элементами a_ij (R) = {1: x_iRx_j; 0: x_i x_j } для всех i и j. Известным примером такого задания отношений являются турнирные таблицы (если ничьи обозначить нулями, как и проигрыш, то матрица изобразит отношение “ x_i – победитель x_j ”).

Третий способ – задание отношения графом. Вершинам графа G (R) ставят в соответствие (пронумерованные) элементы множества X, и если x_iRx_j, то от вершины x_i проводят направленную дугу к вершине x_j; если же x_i x_j, то дуга отсутствует.

Для определения отношений на бесконечных множествах используется четвертый способ – задание отношения R сечениями. Множество

R ⁺(x) = { y Î X | (y, x) Î R }

называется верхним сечением отношения R, а множество

R ^–(x) = { y Î X | (x, y) Î R }

– нижним сечением. Иначе говоря, верхнее сечение – это множество всех y Î X, которые находятся в отношении yRx с заданным элементом x Î X, а нижнее сечение – множество всех y Î X, с которыми заданный элемент x находится в отношении R. Отношение однозначно определяется одним из своих сечений.

Приведенные ниже примеры иллюстрируют все четыре способа представления конкретных отношений.

Пример 1. Полное бинарное отношение U:

1) в U входят все пары (x_i, x_j), x_s Î X;

2) a_ij (U) = 1 для всех i и j;

3) граф G (U) такой, что его дуги соединяют любую пару вершин (стрелки направлены в обе стороны, поскольку x_i U x_j и x_jU x_i, а каждая вершина имеет петлю: x_i U x_i);

4) R ⁺(x) = R ^–(x) = X для любого x Î X.

Пример 2. Диагональное отношение E:

1) в E входят только пары с одинаковыми номерами: x_i E x_j верно только при i = j;

2) a_ij (E) = { 1: i = j; 0: i?? j };

3) граф G (E) такой, что каждая его вершина имеет петлю, а остальные дуги отсутствуют;

4) R ⁺(x) = R ^–(x) = x для любого x Î X.

ОТНОШЕНИЯ ЭКВИВАЛЕНТНОСТИ, ПОРЯДКА И ДОМИНИРОВАНИЯ

Для теории выбора особое значение среди всех бинарных отношений имеют отношения, которые соответствуют предпочтению одной альтернативы перед другой или случаю невозможности отдать предпочтение одной из двух альтернатив. Эти отношения можно задать через строго определяемые отношения эквивалентности, порядка и доминирования.

Для их определения нам понадобятся некоторые свойства отношений вообще*. Бинарное отношение R на множестве X называется:

рефлексивным, если xRx для каждого x Î X;

антирефлексивным, если x x " x Î X (т.е. R может выполняться только для несовпадающих элементов);

симметричным, если xRy Þ yRx " x, y Î X;

асимметричным, если xRy Þ y x " x, y Î X (ясно, что асимметричное отношение R антирефлексивно);

антисимметричным, если для всех x, y Î X (xRy, yRx) Þ x = y;

BINARY RELATION бинарное отношение PREFERENCE PATTERN граф предпочтений RELATION MATRIX матрица отношения ORDERED PAIRS упорядоченные пары UTILITY FUNCTION функция полезности     Обратите внимание на очень важное предположение в языке бинарных отношений – независимость упорядочения двух альтернатив от любой третьей. Это предположение существенно для всей теории. В ее приложениях важно убедиться, что оно выполняется в изучаемом варианте выбора.

транзитивным, если для всех x, y, z Î X (xRy, yRz) Þ xRz;

отрицательно транзитивным, если отношение транзитивно;

сильно транзитивным, если отношение R одновременно транзитивно и отрицательно транзитивно.

Теперь можно охарактеризовать отношения, используемые в теории выбора.

Отношение R на множестве X называется отношением эквивалентности (обозначение ~), если оно рефлексивно, симметрично и транзитивно. Примеры отношений эквивалентности: “быть четным”, “иметь одинаковый остаток от деления на 3” – на множестве натуральных чисел; “быть одноклассниками” – на множестве учеников данной школы; “быть подобными” – на множестве многоугольников. Задание отношения эквивалентности равносильно разбиению множества X на непересекающиеся классы ( при i? j) эквивалентных элементов: x ~ y тогда и только тогда, когда x, y Î X_i (т.е. если x и y принадлежат одному классу эквивалентности).

Отношением нестрогого порядка (обозначение £) называется рефлексивное, антисимметричное и транзитивное отношение. Отношением строгого порядка (обозначение <) называется антирефлексивное, асимметричное и транзитивное отношение. Отношение нестрогого порядка можно рассматривать как объединение отношений < и ~.

Наконец, отношением доминирования называется отношение, обладающее антирефлексивностью и асимметричностью. Говорят, что “ x доминирует y ” (обозначается x» y), когда x в каком-то смысле превосходит y. (Очевидно, строгий порядок – частный случай доминирования, при котором имеет место еще транзитивность.)

7.4 ————— Пример графа предпочтений

Хотя при подробном рассмотрении выбора потребуются и другие факты теории отношений, введенные понятия позволяют составить представление о возможностях данного языка.

В случае конечных множеств X очень удобно находить наилучшие альтернативы с помощью графа предпочтений, стрелки которого направлены в сторону менее предпочтимой альтернативы (рис. 7.4). Выделив вершины графа, из которых стрелки только исходят (альтернативы 6 и 10 на рис. 7.4), мы находим недоминируемые, т.е. наилучшие, альтернативы. Можно показать, что если граф сильно транзитивен (т.е. транзитивен и по наличию, и по отсутствию стрелок) и антирефлексивен (отсутствуют петли), то описываемый выбор сводится к однокритериальному выбору. Другие типы графов описывают другие ситуации выбора.

Несмотря на то что язык бинарных отношений введен для описания более общих и сложных ситуаций, нежели те, которые описываются критериальным языком, в чисто познавательных целях поучительно проследить, как уже известная нам ситуация выглядит в новом представлении.

Например, многомерное критериальное пространство (с теми оговорками о соотношении размерностей критериев, которые были сделаны в предыдущем параграфе) может быть поставлено в соответствие евклидову пространству. Введение на этом пространстве бинарных отношений требует учета его свойств. В частности, начинают играть роль отношения инвариантные (относительно переноса), для которых верхнее сечение в любой точке может быть получено параллельным переносом верхнего сечения в любой другой точке. Примером инвариантного отношения является отношение Парето P:

.

7.5 ————— Описание паретовского множества как множества таких альтернатив, для которых верхнее сечение P+(x) пусто.

Верхнее сечение отношения P есть первый квадрант с началом в точке x; теперь понятно, как находится паретовское множество альтернатив (на рис. 7.5 приведен случай конечного множества X; сравните этот рисунок с рис. 7.1, г): в паретовское множество включаются альтернативы, верхнее сечение которых пусто (на рис. 7.5 они отмечены кружками).

В общем же случае выделение наиболее предпочтительных альтернатив возможно с помощью понятия оптимальности по отношению R, позволяющего придавать разный смысл понятию “наилучший” (задавая разные отношения R). Элемент x Î X называется мажорантой по отношению R на X, если для всех y Î X выполнено условие y x. Множество X ₊(R) всех мажорант называется множеством R -оптимальных элементов.

ОБ ОЦИФРОВКЕ ПОРЯДКОВЫХ ШКАЛ

Важно обсудить ситуацию, возникшую при описании выбора на языке бинарных отношений в результате создания теории полезности [38]. П. Фишберн строго доказал теорему, смысл которой довольно ясен: если множество X конечно и между его элементами имеется отношение строгого порядка, то можно построить такую вещественную функцию u (x) на X, для которой

(x < y) Þ [ u (x) < u (y)]

(в левой части < означает отношение предпочтения, в правой – знак “меньше”).

Функция u (x) называется функцией полезности. Ясно, что такая функция не единственна: произвольное монотонное преобразование сохраняет ее упорядочивающее свойство. Этот результат затем был обобщен на счетные и континуальные множества X, на нестрогий порядок и на многокритериальный случай (аддитивные функции полезности). Определение функции u (x) позволяет перейти от языка бинарных отношений к критериальному языку, взяв u (x) в качестве критериальной функции. Были развиты методы, позволяющие сузить класс функций полезности, например благодаря рассмотрению иерархических парных предпочтений (см. § 6.2), повышая тем самым “точность определения u (x)”.

Создается впечатление, что от качественных порядковых измерений можно перейти к количественным. На самом деле мы здесь вновь сталкиваемся с такой ситуацией, когда “оцифровка” порядковой шкалы не делает ее числовой шкалой. Для воспроизводства упорядочения фиксированного попарно упорядоченного множества X, конечно, можно воспользоваться числовой функцией u (x); однако стоит дополнить X альтернативами, которые не рассматривались при первом упорядочении, как функцию u (x) потребуется определять заново. Более того, если два разных эксперта дадут разные упорядочения множества X, то можно доопределить функции полезности для каждого из них, но сравнивать их численно иначе как в отношении порядка не имеет смысла (см. пример в § 6.2), хотя обе они определены на одном множестве.

В тех случаях, когда количественная величина по каким-то причинам измеряется в порядковой шкале, оцифровка порядковых данных могла бы иметь смысл. Однако во многих приложениях теории полезности мы имеем дело с измерениями, которые в принципе не могут выйти из разряда порядковых.

Подведем итог В ряде практических случаев критериальная функция не существует, т.е. оценку данной альтернативе можно дать только в результате ее сравнения с другой альтернативой. Это потребовало более общего описания выбора. Первым таким обобщением и является язык бинарных отношений.

Summary In many cases no criterion function exists because an evaluation of a given alternative may be made only by comparing it with another alternative. This requires a more general description of the choice. The language of binary relations is such a generalization.

ЯЗЫК ФУНКЦИЙ ВЫБОРА

Некоторые особенности выбора привели к построению третьего, еще более общего языка его описания. Во-первых, нередко приходится сталкиваться с ситуациями, когда предпочтение между двумя альтернативами зависит от остальных альтернатив. Например, предпочтение покупателя между чайником и кофеваркой может зависеть от наличия в продаже кофемолки. Во-вторых, возможны такие ситуации выбора, когда понятие предпочтения вообще лишено смысла. Например, по отношению к множеству альтернатив довольно обычными являются правила выбора “типичного”, выбора “среднего”, выбора “наиболее отличного, оригинального”, теряющие смысл в случае двух альтернатив.

ФУНКЦИИ ВЫБОРА КАК МАТЕМАТИЧЕСКИЙ ОБЪЕКТ

Язык функций выбора описывает выбор как операцию над произвольным множеством альтернатив X, которая ставит этому множеству в соответствие некоторое его подмножество C (X): C (X) Í X. (Обозначение связано с первой буквой английского слова choiсe – “выбор”.) Функция выбора как отображение совокупности множеств в совокупность множеств (поскольку для выбора могут предлагаться любые подмножества X_i Í X) без поэлементного отображения одного множества на другое и без отображения множеств на числовую ось является своеобразным и пока еще не полно изученным математическим объектом. Конечно, накладывая на функцию выбора определенные требования, мы можем на этом языке описывать и те варианты выбора, которые отражаются в предыдущих языках. Однако главное достоинство нового языка – возможность рассмотрения более сложных правил выбора. На такую возможность указывает хотя бы различие числа возможных функций выбора и числа возможных графов предпочтения на множестве n альтернатив. Число графов, отличающихся наличием или отсутствием хотя бы одной дуги, равно . Если для выбора предлагаются k из n альтернатив, то число функций выбора равно 2 ^k (каждая из альтернатив может либо входить в C (X_k), либо нет). Так как число возможных вариантов предъявления альтернатив равно , то общее число функций выбора равно . Как видим, разнообразие функций выбора намного превосходит разнообразие графов предпочтения. Кроме того, здесь сразу допускается отказ от выбора, т.е. пустой выбор C (X_i) =?? что также расширяет множество правил выбора.

ОГРАНИЧЕНИЯ НА ФУНКЦИИ ВЫБОРА

Различие между классами правил выбора можно выразить через различные ограничения, которым подчиняется тот или иной тип функции выбора. Отдельные ограничения и их комбинации дают уже известные нам правила выбора, другие определяют новые правила, которые предстоит изучить. (По разным причинам наиболее подробному рассмотрению подвергались именно те функции выбора, которые идентичны выбору, описываемому на предыдущих языках [22].) Приведем некоторые из таких ограничений:

Аксиома наследования (Н):

X' Í X Þ C (X') Ê C (X) Ç X'.

Смысл этой аксиомы сводится к требованию, чтобы в выбор на подмножестве X' вошли все те альтернативы из X', которые входили в выбор на X (возможно, еще и другие; рис. 7.6, а).

Аксиома согласия (С):

Это означает, что в выбор из объединения множеств обязательно должны входить альтернативы, общие для выборов из всех множеств (и, возможно, другие альтернативы; рис. 7.6, б).

Оказывается, совместное подчинение функции выбора аксиомам Н и С дает выбор, описываемый в языке бинарных отношений.

Аксиома отбрасывания (O):

C (X) Í X' Í X Þ C (X') = C (X).

Это означает, что если отбросить любую часть отвергнутых при выборе альтернатив, то выбор на оставшемся множестве не изменится (рис. 7.6, в); поэтому данную аксиому называют также условием независимости от отвергнутых альтернатив.

Совместное наложение на выбор аксиом Н, C и O приводит к случаю выбора паретовского множества.

Аксиома Плотта (КС):

C (X ₁ È X ₂) = C (C (X ₁) È C (X ₂)).

Это отражает требования, накладываемые при многоступенчатых выборах, когда считается, например, что определить чемпиона мира можно путем соревнований между чемпионами стран и результат окажется тем же, если соревноваться будут не только чемпионы (рис. 7.6, г). Поэтому эту аксиому называют еще условием независимости от пути. Функции выбора, удовлетворяющие ей, называются квазисумматорными.

Можно показать, что требование КС эквивалентно совместному выполнению Н и O; следовательно, соединение требований КС и С тоже приводит к паретовскому выбору.

Аксиома предпочтения (П):

X' Í X Þ C (X) Ç X' = C (X').

7.6 ————— Иллюстрация различных аксиом, накладываемых на функции выбора

Она требует, чтобы при сужении множества альтернатив в выборе оставались только те альтернативы, которые входили в выбор ранее (рис. 7.6, д). Это столь жесткое ограничение, что оно эквивалентно скалярному критериальному выбору.

Ясно, что некоторые из введенных аксиом можно ослаблять или усиливать (например, П есть усиление Н). Аксиому Плотта можно усилить до аксиомы сумматорности: C (X ₁ È X ₂) = C (X ₁) È C (X ₂); можно накладывать новые, независимые требования (например, аксиома мультипликаторности C (X ₁ Ç X ₂) = C (X ₁) Ç C (X ₂), аксиома монотонности X ₁ Í X ₂ Þ Þ C (X ₁) Í C (X ₂); рис. 7.6, е), получая при этом различные типы выбора. Наоборот, можно, изучив ограничения того или иного реального правила выбора, искать свойства класса функций выбора, удовлетворяющего этим ограничениям (попробуйте, например, установить, каким аксиомам отвечает и противоречит правило определения победителя шахматного турнира по числу набранных очков). Айзерман с сотрудниками начал изучение классов функций выбора [2]; эту работу пока нельзя считать законченной.

 

Подведем итог Язык функций выбора является весьма общим и потенциально может описать любой выбор. Однако его теория находится в начальной стадии развития и пока еще занимается преимущественно описанием старых ситуаций в новых терминах

Summary The language of choice functions is very general and can potentially describe any type of choice. However, its theory is only beginning to be developed and is still occupied with describing old situations in new terms.

ГРУППОВОЙ ВЫБОР

В человеческом обществе единоличное принятие решений является не единственной формой выбора. “Ум – хорошо, а два – лучше”, гласит поговорка, имеющая в виду тот случай, когда оба ума с одинаковыми намерениями пытаются найти хороший выбор. Этот случай мы и рассмотрим в данном параграфе (выбор в условиях конфликта будет рассмотрен в дальнейшем).

ОПИСАНИЕ ГРУППОВОГО ВЫБОРА

Итак, пусть на множестве альтернатив X задано n в общем случае различных индивидуальных предпочтений (для определенности будем говорить о бинарных отношениях) R ₁, R ₂,..., R_n. Ставится задача о выработке некоторого нового отношения R, которое согласует индивидуальные выборы, выражает в каком-то смысле “общее мнение” и принимается за групповой выбор. Очевидно, что это отношение должно быть какой-то функцией индивидуальных выборов: R = F (R ₁,..., R_n). Различным принципам согласования будут отвечать разные функции F. В принципе, т.е. теоретически, функции F могут быть совершенно произвольными, учитывать не только индивидуальные выборы, но и другие факторы, в том числе и исход некоторых случайных событий (например, бросания жребия), и главный вопрос состоит в том, чтобы правильно отобразить в функции F особенности конкретного варианта реального группового выбора.

РАЗЛИЧНЫЕ ПРАВИЛА ГОЛОСОВАНИЯ

Один из наиболее распространенных принципов согласования – правило большинства: принятой всеми считается альтернатива, получившая наибольшее число голосов. Правило большинства привлекательно своей простотой и демократичностью, но имеет особенности, требующие осторожного обращения с ним. Прежде всего оно лишь обобщает индивидуальные предпочтения, и его результат не является критерием истины. Только дальнейшая практика показывает, правильным или ошибочным было решение, принятое большинством голосов; само голосование – лишь форма согласования дальнейших действий*. Во-вторых, даже в простейшем случае выбора одной из двух альтернатив легко представить себе ситуацию, когда правило большинства не срабатывает: разделение голосов поровну при четном числе голосующих. Это порождает варианты: “председатель имеет два голоса”, “большинство простое (51 %)“, “подавляющее большинство (около 3/4)“, “абсолютное большинство (близкое к 100 %)“, наконец, “принцип единогласия (консенсус, право вето)“.

—————————— * Этот вопрос, однако, формально находится вне нашего рассмотрения: ведь пока мы обсуждаем выбор в условиях определенности, а здесь речь зашла о выборе определенной альтернативы с неопределенными последствиями. Такие задачи мы рассмотрим позже.

VOTING голосование GROUP CHOICE групповой выбор CONSENSUS консенсус MAJORITY RULE правило большинства CHOICE FUNCTION функция выбора     Язык функций выбора (“глобальных функций множеств”) описывает результат выбора как некоторое подмножество множества альтернатив. Такое соответствие двух множеств без их поэлементного соответствия является новым понятием, расширяющим смысл термина “функция”. Оно позволяет описывать произвольные ситуации выбора, чего нельзя было сделать с помощью предыдущих двух языков. Коллективный выбор при любом правиле его осуществления сопряжен с риском оказаться в парадоксальной ситуации. Знание парадоксов голосования необходимо для предотвращения искажения демократического характера этой процедуры.

Подчеркнем, что при любом из этих вариантов подразумевается отказ от принятия решения, если ни одна из альтернатив не получила необходимого процента голосов. Поскольку в реальной жизни отказ от дальнейших действий, следующих за решением, бывает недопустим, а переход к принятию за групповой выбор выбора отдельного лица (“диктатора”) – нежелательным, разрабатываются различные приемы, сокращающие число ситуаций, приводящих к отказу.

Например, если два эксперта дали противоположные предпочтения между двумя вариантами a и b, то можно сделать выбор, сравнивая “силу предпочтения” каждого эксперта. При возможности введения количественного критерия оценки это сводится к арифметической операции, но и при порядковом сравнении есть возможность оценки “силы предпочтения”. В криминалистической практике в таких случаях экспертам предлагается в одном ряду с a и b упорядочить по предпочтению еще несколько альтернатив, скажем c, d и e. Пусть первый эксперт дал упорядочение (c, d, a, b, e), а второй – (b, c, d, e, a). Тогда можно сделать вывод, что степень предпочтения b по сравнению с a у второго эксперта больше, чем степень предпочтения a перед b у первого, и принять решение в пользу b (за этим приемом стоит ряд предположений – сравнимость интенсивностей предпочтений, одинаковая компетентность экспертов и т.д., требующих проверки в ответственных случаях).

Даже для консенсуса, требующего единогласия, разработаны приемы, облегчающие его достижение. Так, Р. Акофф отмечает:

“Консенсус часто трудно достижим, но редко невозможен. Я обнаружил, что в трудных случаях очень эффективна следующая процедура. Первое – максимально уточнить формулировки альтернатив, между которыми консенсус не допускает выбора. Второе – коллективно построить тест эффективности альтернатив и принять консенсусом решение, что данный тест справедлив и что все согласны следовать его результату. Третье – провести тест и использовать его результат. Я смог успешно применить эту процедуру даже в таком случае, когда законодатели одного государства не могли прийти к согласию, вводить или нет смертную казнь за убийство. В результате обсуждения члены законодательного органа пришли к согласию, что они все имеют одну цель – минимизировать число жертв убийств. Как только такое согласие было достигнуто, проблема была сведена к конкретному вопросу: уменьшает ли введение смертной казни число убийств? Все согласились, что необходимо провести исследование, отвечающее на этот вопрос. Такое исследование было проведено и его результаты использованы (оно показало, что число убийств в ряде государств до и после отмены или введения смертной казни заметно и значимо не изменялось)” [44].

Если же не удавалось достичь консенсуса не только по поводу самих альтернатив, но и относительно способа их проверки, то, по мнению Акоффа, следует найти консенсусное решение, что же делать дальше. Интересно его наблюдение, что в таких случаях обычно принималось решение поручить выбор одному из авторитетных и ответственных лиц (мы еще вернемся к этому моменту). Фактически это переход от демократического, но не давшего решения правила голосования к недемократическому, но приводящему к какому-то решению “диктаторскому” принципу. Такое экспериментальное наблюдение имеет и теоретическое объяснение, излагаемое ниже на качественном уровне.

ПАРАДОКСЫ ГОЛОСОВАНИЯ

Итак, следующая особенность правила голосования – это возможность отказа от выбора из-за недостижения требуемого большинства. Казалось бы, исключив такую возможность, можно обеспечить принятие решения в любых случаях. Например, пусть три эксперта большинством голосов решают вопрос, какая из двух альтернатив более предпочтительна. При такой постановке вопроса они действительно не могут не сделать выбор. Однако здесь мы приходим к еще одной особенности правила голосования – его нетранзитивности.

Пусть, например, каждая из трех группировок законодателей, образующих большинство лишь попарно, выдвинули свой вариант законопроекта: a, b и c. Или три парня заспорили, чья девушка лучше, и намереваются решить спор голосованием. Чтобы гарантировать большинство на каждом шаге процедуры, альтернативы предъявляются попарно. Каждая сторона руководствуется при этом своим набором предпочтений; пусть это соответственно последовательности (a > b > c), (b > c > a) и (c > a > b).

После голосования по паре (a, b) в результате получаем два голоса против одного: a > b; по паре (b, c) имеем b > c; по паре (c, a) имеем c > a. Голосование большинством не привело к выяснению “общепризнанного” порядка альтернатив: a > b > c > a. В случае же применения процедуры, при которой после рассмотрения очередной пары отвергаемая альтернатива заменяется новой, окончательно принятое решение зависит от порядка предъявления альтернатив: при порядке (a, b, c) выбирается c; при порядке (b, c, a) выбор остановится на a; при порядке (a, c, b) – на b. Если таким образом принять законопроект, то чье мнение он будет выражать – большинства или организатора голосования? Очевидно, что такие решения не отвечают идеалу согласованного группового выбора.

Причина данного парадокса нетранзитивности группового выбора состоит, конечно, в цикличности совокупности исходных индивидуальных предпочтений. Однако это лишь частный пример более общего явления, получившего название парадокса Эрроу (или теоремы о невозможности). Не вдаваясь в подробности этой теоремы и ее доказательства, изложим ее смысл.

Из всевозможных функций F индивидуальных выборов R ₁,..., R_n выделим те, которые отвечают требованиям, выражающим наше понимание того, какой выбор можно считать согласованным. Кроме формальных требований

1⁰) “ n ³ 2”, “число альтернатив ³ 3”, “ F определена для любых { R_i }”

естественно также потребовать, чтобы:

2⁰) если в результате группового выбора предпочтение было отдано альтернативе x, то это решение не должно меняться, если кто-нибудь из ранее отвергавших x изменил свое предпочтение в его пользу (условие монотонности);

3⁰) если изменения индивидуальных предпочтений не коснулись определенных альтернатив, то в новом групповом упорядочении порядок этих альтернатив не должен меняться (условие независимости несвязанных альтернатив);

4⁰) для любой пары альтернатив x и y существует такой набор индивидуальных предпочтений, для которого F (R ₁,..., R_n) = (x > y) (условие суверенности; без него возможно навязывание y независимо от порядков предпочтений индивидуумов);

5⁰) не должно быть такого индивидуума, для которого из его предпочтения x > y (при любых x и y) вытекает, что F (R ₁,..., R_n) = (x > y) независимо от предпочтений других индивидуумов (условие отсутствия диктаторства).

Парадокс Эрроу состоит в том, что первые четыре условия противоречат пятому; не существует правила F, удовлетворяющего всем пяти требованиям. Анализ причин такого обескураживающего следствия из столь невинных на вид предположений показывает [21; 24], что основную роль играет возможность циклических множеств ранжирований, что характерно для бинарных отношений, удовлетворяющих условию 3⁰.

Нетранзитивность мажоритарного отношения может проявляться и в других неожиданных формах. Рассмотрим такую задачу [24]. Пусть каждый из n субъектов имеет свою долю a_i общего ресурса Вектор` a = (a <sub>1</sub>,..., a<sub>n</sub>) назовем состоянием системы. Другое состояние` b = = (b ₁,..., b_n) с точки зрения i -го субъекта хуже` a, если a<sub>i</sub> ³ b<sub>i</sub>. Будем теперь производить перераспределение ресурсов на основе очень сильного большинства: система перейдет из` a в` b, если состояние` b не хуже` a для всех, кроме одного (“тотально-мажоритарное правило”). Последовательность состояний` a ₁,` a <sub>2</sub>,...,` a_k будем называть тотально-мажоритарным путем из` a <sub>1</sub> в` a_k, если переходом в очередное состояние удовлетворены все участники, кроме, естественно, того, чей ресурс в данный момент перераспределяется. Пусть теперь заданы два произвольных состояния системы:` a и` b. При каких условиях существует тотально-мажоритарный путь из` a в` b? Оказывается, что такой путь существует всегда. Снова имеем дело с парадоксом: возможны любые перераспределения, и все они выражают мнение “всего общества”, кроме одного субъекта (правда, эти “несогласные” на разных этапах различны).

Задачи группового выбора часто все же могут быть разрешены. Во-первых, в ряде случаев циклические ранжирования могут отсутствовать, либо они не охватывают “наиболее важные” альтернативы, либо принимаются меры по их обнаружению и устранению. Во-вторых, во многих случаях “диктаторский” принцип согласования не является неприемлемым. Это иллюстрируется примером оптимизации по “главному” из нескольких критериев. В других случаях это единственно возможный принцип (например, единоначалие в армии). В-третьих, переход (когда это возможно) к использованию единой числовой, а не порядковых индивидуальных шкал предпочтений может вообще аннулировать проблему нетранзитивности. В-четвертых, в реальных ситуациях мажоритарные правила применяются в комбинации с другими правилами, так что, образовав, например, коалицию, группы субъектов могут блокировать действие голосования.

7.7 ————— Иллюстрация парадокса многоступенчатого голосования при наличии коалиции

Здесь мы приходим к еще одной особенности голосования, которую следует иметь в виду на практике. Речь идет о вмешательстве коалиций в механизм голосования, фактически меняющем его характер. Например, при многоступенчатом голосовании по правилу большинства коалиция, находящаяся в меньшинстве, может добиться принятия своего решения. На рис. 7.7 изображено голосование по три большинством в 2/3 на каждой ступени. Видно, что уже на второй ступени меньшинство может навязывать свое мнение большинству. Если число ступеней не ограничивать, то теоретически побеждающее таким образом меньшинство может быть сколь угодно малым. То, что при многоступенчатом голосовании может победить кандидат, не набравший действительного большинства голосов, происходит и в действительности. Например, в 1876 г. президентом США был избран Р.Б. Хейес (185 голосов выборщиков), а не С. Дж. Тилден (184 голоса), хотя на долю последнего пришлось 51% голосов всех избирателей. Такие же ситуации имели место в президентских выборах 1874 и 1888 гг.

 

Подведем итог Общественная практика ставит проблему группового выбора, в котором могли бы принять участие все члены социума. Один из простых и популярных способов коллективного выбора – голосование. Эта широко применяемая и во многих случаях успешная процедура наряду с очевидными достоинствами обладает рядом скрытых особенностей, которые могут ослабить и даже извратить демократический характер голосования. Знание таких “парадоксов” голосования необходимо не только специалистам по системам.

Summar y The ideals of democrac y gives rise to the problem (among others) of group choice, in which all members of societ y can take part. One simple and popular procedure of collective choice is voting. This widel y used and often successful procedure has, besides its evident virtues, some latent features that could weaken and even pervert the democrac y of voting. Knowledge of such “paradoxes” of voting is necessar y, and not onl y for s y stems scientists.

⇐ Предыдущая13141516171819202122Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: