Выбор при расплывчатой неопределенности

Любая задача выбора является задачей целевого сужения множества альтернатив. Как описание альтернатив (перечень их признаков, параметров и т.п.), так и описание правил их сравнения (критериев, отношений) даются в терминах той или иной измерительной шкалы (см. § 6.2). Известно, что любая измерительная шкала допускает размытие (см. § 6.3). Точнее говоря, в жизни мы часто сталкиваемся с ситуациями, описать которые можно лишь в размытых шкалах. Это, разумеется, относится и к ситуациям, приводящим к выбору. В результате мы приходим к задачам выбора в условиях расплывчатой неопределенности. Каждой из задач, рассмотренных в предыдущих параграфах, можно поставить в соответствие несколько расплывчатых задач, поскольку размытыми могут оказаться все или только некоторые компоненты задачи. До настоящего времени рассмотрено лишь незначительное число таких задач, однако ведется работа в этом направлении.

МНОГОКРИТЕРИАЛЬНЫЙ ВЫБОР В РАСПЛЫВЧАТОЙ СИТУАЦИИ

Уже в первой работе по принятию решений в расплывчатой ситуации Беллман и Задэ [4] выдвинули идею, состоящую в том, чтобы и цели, и ограничения представлять как размытые множества на множестве альтернатив (в случае одной цели и одного ограничения это соответствует заданию множеств G = { x,? _G (x)} и C = { x,? _C (x)}). Следующий важный шаг состоял в определении размытого решения D как пересечения размытой цели G и размытого ограничения C, т.е. (см. § 6.3)

? _D (x) = min [? _G (x),? _C (x)]. (1)

CONSTRAINT ограничение OPTIMAL оптимальный FUZZ Y расплывчатый DISTANCE расстояние COMPARISON сравнение   Правила выбора в расплывчатой ситуации, естественно, являются различными в зависимости от того, что именно расплывчато в этой ситуации. Задача выбора решается просто и изящно, если критериальные функции отождествляются с функциями принадлежности. Однако на практике встречаются и другие задачи; например, расплывчатым может быть любой параметр критериальной функции, которая сама не является функцией принадлежности.

Обобщение на случай большего числа условий очевидно. Если из размытого множества D требуется выделить какую-то одну альтернативу, то можно поступать по-разному (вплоть до рандомизации выбора), но возможный вариант состоит в максимизации? _D (x):

. (2)

При таком изложении задачи выбора напрашивается идея о том, чтобы вообще функцию принадлежности i -му условию интерпретировать как i -й критерий качества и вернуться к многокритериальным задачам. Тогда соотношение (1) оказывается формой суперкритерия (1) § 7.2, которая далеко не единственна.

Интересны исследования в этом направлении, сделанные Эстером [45]. Он рассмотрел суперкритерий вида

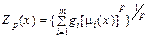, (3)

где 0 £ g_i £ 1, 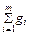= 1; m – число размытых условий;? _i (x) – функция принадлежности i -му условию; p – параметр суперкритерия. Представление (3) интересно не только наличием свойств, облегчающих математическое рассмотрение задачи (например, монотонность и непрерывность по всем компонентам), но и тем, что оно охватывает широкий класс частных суперкритериев. Так, при p ® – ¥ получается оператор нахождения минимального элемента из заданной совокупности (т.е. снова приходим к формуле (1)), при p = 0 – оператор умножения, при p = 1 – оператор сложения, при p ® + ¥ – оператор нахождения максимального элемента. Итак, задача нахождения наилучшей альтернативы x * сводится к максимизации Z_p (x):

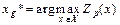. (4)

Очевидно, что при этом решение зависит от конкретного набора коэффициентов g = { g_i }. Обозначим через E (p) множество { x_g *}, соответствующее разным g при фиксированном p. Эстер обнаружил [46] интересные свойства множеств E (p): для всех – ¥ < p ₁ £ p ₂ < ¥ справедливо включение E (p ₂) Í E (p ₁) Í РМ, где РМ – паретовское множество (см. § 7.2).

Функции принадлежности вообще находить непросто (см. § 6.3), а при использовании изложенного подхода, кроме того, требуется, чтобы они еще имели и смысл критериальных функций в задаче выбора. Это может оказаться и неудобным, и бессмысленным. С.А. Орловский [27] предложил не изменять содержательного смысла критериев качества альтернатив и не отождествлять критериальные функции с принадлежностными, а отразить в модели расплывчатость шкал, в которых эти критерии фиксируются (если такая расплывчатость имеет место). Предполагается, что критериальные функции q_i (x) относятся к параметрическим семействам, т.е. q_i (x) = J_i (x,` q), и считается, что расплывчатость критериальных функций сводится к расплывчатости в описании параметров` q: Q = {` q,? <sub>Q</sub> (q) }. Теперь для каждой альтернативы x значение критерия J<sub>i</sub> (x,` q) принадлежит размытому множеству, функция? _i (J_i (x)) принадлежности к которому зависит от x и от конкретного вида функций J_i (x,` q) и? <sub>Q</sub> (` q). Носитель этого множества может быть как ограничен сверху величиной J_i ⁰(x), так и не ограничен (чем больше J_i, тем лучше; ограниченность J_i сверху несущественна). Если естественного ограничения снизу нет, то его можно ввести искусственно, задав некоторый уровень? (0 <? < 1) для функции принадлежности и взяв в качестве J_i ⁰(x) наименьший корень уравнения? _i (J_i (x)) =?. В результате величины J_i ⁰(x),..., J_m ⁰(x) можно рассматривать как новые (и уже неразмытые!*) критериальные функции, и мы возвращаемся к стандартной многокритериальной задаче, которую можно решать любым из стандартных методов (см. § 7.2). Орловский, в частности, предлагает находить паретовское множество альтернатив.

Заканчивая обзор расплывчатых вариантов критериальных задач выбора, рассмотрим еще задачи, связанные с использованием расстояний между точками в пространстве альтернатив. При расплывчатом описании альтернатив предлагается “расстояние” определять через модули разностей функций принадлежности, например

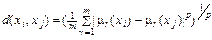, (5)

где? _r (x) – функция принадлежности по r -му признаку к интересующему нас множеству. Такие расстояния используются в задачах классификации [17].

НЕКРИТЕРИАЛЬНЫЕ ЗАДАЧИ РАСПЛЫВЧАТОГО ВЫБОРА

Некоторые успехи имеются и в рассмотрении расплывчатых вариантов выбора, описываемого на языке бинарных отношений (см. § 7.3). Во-первых, сделано расплывчатое обобщение отношения предпочтения [49]. Размытое отношение R слабого порядка определяется как удовлетворяющее размытым условиям связности и транзитивности:

x_i ¹ x_j Þ m _R (x_i, x_j) > 0 или? _R (x_j, x_i) > 0 (6)

(связность);

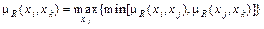(7)

(транзитивность).

Если условие (6) заменить условием

m _R (x_i, x_j) >0 Þ? _R (x_j, x_i) = 0 (8)

(асимметрия), то такое упорядочение называется сильным.

Во-вторых, Л. Задэ показал [30], что любое расплывчатое отношение R допускает разложение по? в виде объединения неразмытых множеств R _? с функциями принадлежности

(9)

где 0 <? < 1 (что можно представить как расслоение объема под? _R на горизонтальные пласты уровней?).

Это, например, позволяет перейти от расплывчатого описания коллективного упорядочения альтернатив к нерасплывчатому множеству альтернатив, отобранных “со степенью согласия на уровне?” [49].

О других классах задач выбора кратко можно сказать следующее.

Расплывчатой версии языка глобальных функций множеств (описанного в § 7.4) пока не создано.

Начато исследование различий и аналогий между статистической и размытой неопределенностями. Некоторые особенности, возникающие при одновременном наличии обеих неопределенностей, рассмотрены, например, в [26]. Не углубляясь в детали (так как для этого понадобилось бы использовать достаточно сложные построения, связанные с понятием случайных множеств), отметим, что в целом идеи теории расплывчатых множеств привлекают все больший интерес, поскольку в этой модели удалось отразить многие особенности языковых моделей и действий человека на их основе.

Подведем итог Ряд ситуаций выбора характеризуется расплывчатой неопределенностью. Рассмотрено несколько различных вариантов таких ситуаций; функции принадлежности в них имеют разный смысл (либо сами служат критериями, либо описывают размытость некоторого параметра критериальной функции). Естественно, это приводит к разным алгоритмам выбора.

Summary The uncertainty of some decision situations is described as fuzziness. Several variants of such situations are considered, with different meanings of the fellowship function (it can either be identified with the criterion function, or it can describe the fuzziness of a certain parameter of the criterion function). Naturally, this leads to different algorithms of choice.

⇐ Предыдущая16171819202122232425Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: