Построение графиков с помощью табличного процессора.

Все графики должны быть оформлены в одном стиле:

· Подписаны оси с указанием наименования и размерности физической величины,

· Сделана разметка осей,

· Подписан график в целом.

Графики должны отражать зависимость изучаемых величин от различных факторов, согласно теории, изложенной в пояснительной записке.

Студент должен уметь: с помощью средств табличного процессора строить графики (в том числе несколько в одной системе координат), выбирать масштаб осей, оформлять графики и оси.

Преподаватель оценивает: Навыки работы с табличным процессором: считывать данные из файла, строить диаграммы (графики). Соответствие построенных графиков теории, изложенной в пояснительной записке, оформление графиков.

Отчетные документы:

1. Файлы, созданные табличным процессором, содержащие расчетные данные и диаграммы (графики), построенные на их основе.

Оформление работы.

На данном этапе студент должен завершить написание научной работы, включив в нее описание результатов, их обсуждение и выводы. При разработке и отборе материала, нужно ориентироваться на текст задачи, поставленные там вопросы. Изложение материала в работе должно быть последовательным, из него должны логически следовать выводы. Также необходимо сравнить результаты моделирования с изложенной в начале работы теорией, ответить на все вопросы, поставленные в задании, написать введение и заключение.

Студент должен оформить работу по следующему плану:

1. Титульный лист (см. образец)

2. Содержание работы (оглавление с указанием наименования параграфов и номера страниц)

3. Литературный обзор по решаемой задаче.

4. Описание и обсуждение результатов компьютерного моделирования (решения системы ОДУ), сравнение полученных результатов с теорией.

5. Список используемой литературы.

Преподаватель оценивает: Правильность оформления работы, логику и полноту содержания.

Отчетные документы:

1. Файл «Фамилия_студента.odt», оформленный в соответствии с требованиями.

Создание презентации к устному докладу

На данном этапе студент должен освоить работу с программой создания презентаций: Создание простых слайдов, работу с разметкой слайда, создание фона слайда, форматирование текста, создание автофигур, размещение изображений на слайде, настройку анимации объектов слайда, редактирование презентации в целом (работу с различными режимами программы). Затем, используя полученные навыки, студент готовит презентацию доклада по индивидуальной задаче (см. образец).

Преподаватель оценивает: Оформления презентации, ее соответствие содержанию работы.

Отчетные документы:

1. Файл «Фамилия_студента.odp», содержащий презентацию к докладу по решенной задаче.

Работа с базой данных.

На данном этапе студент должен освоить работу с базами данных: создание новой базы и таблиц с помощью мастера, создание первичного ключа, поиск информации в базе, формирование запроса на поиск конкретной информации. Студент должен найти в общей базе данных информацию по литературе к его задаче.

Преподаватель оценивает: Навыки работы с базой данных, соответствие найденной информации заданию.

 

Порядок выполнения работы

1. Получите задачу у преподавателя.

Прочитайте внимательно условие. Прежде чем приступить к выполнению задания, необходимо найти ответы на вопросы по следующему плану:

1) В каком разделе физики изучается явление (закон);

2) Какое физическое явление или закон лежат в основе данной задачи;

3) История изучения (открытия) этого явления или закона:

a) Кем и когда открыт (изучен);

b) Какие наблюдения (факты, опыты) легли в основу открытия;

c) Какие предположения были выдвинуты первоначально.

4) Запишите современную формулировку явления (закона), основные уравнения, описывающие явление (закон).

1. Используйте поисковые системы Интернета для ответов на поставленные вопросы.

Поиск с помощью подборок ссылок.

Обычно на сайте (странице), посвященном какой-либо теме, существуют подборки ссылок по данной теме. Однако есть специализированные страницы, на которых выставляются ссылки по различным темам. Ссылки по физике можно найти на страницах:

· http://www.curator.ru/physics/

· http://www.fio.vrn.ru/2005/7/!Physics/2/c.htm

· http://www.tula.net/tgpu/resources/Physics_internet/demo.htm

· http://edu.tomsk.ru/teacher_help/phis_sites.htm

· http://www.benran.ru/E_n/PHISINT.HTM

1. Литературный обзор

Напишите литературный обзор по предложенному выше плану с учетом требований к оформлению большого документа.

Обыкновенные дифференциальные уравнения

Краткая теория

Постановка задачи

Обыкновенными дифференциальными уравнениями (ОДУ) называются уравнения вида F(x, y, y’, y”, … y⁽ⁿ⁾) = 0

Где 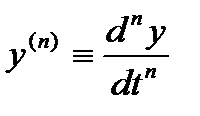- производная n-того порядка. Порядком ОДУ называется номер старшей производной, входящей в это уравнение.

Общим решением этих уравнений является семейство функций

у = y(x, C₁, C₂,…).

Константы C₁, C₂, … определяются из дополнительных условий, налагаемых на функцию y(x) и ее производные. Число дополнительных условий равно порядку ОДУ. Вычисляя из дополнительных данных значения С₁, С₂, С₃, ¼, С_n из общего решения получим частное решение.

Если все дополнительные условия заданы в одной точке х, то они называются начальными, а совокупность ОДУ с начальными условиями – задачей Коши.

у(x₀) = у₀

у’(x₀) = z₁

¼¼¼

y^(n-1)(x₀) = z_n-1

Если дополнительные условия заданы в разных точках х, то они называются граничными, а совокупность ОДУ с граничными условиями – краевой задачей. Например, дополнительные условия могут представлять собой значения искомой функции в разных точках:

y(x₀) = y₀

y(x₁) = y ₁

¼¼¼

y(x_n-1) = y_n-1,

Дополнительные условия могут содержать и значения производных в некоторых точках.

Для численного решения ОДУ разработано много так называемых разностных схем. В них ОДУ заменяется алгебраическими уравнениями для функции y(x, C₁, C₂, …) в некоторых точках х_i. Обычно, для применения этих схем необходимо ОДУ разрешить относительно старшей производной. Для ОДУ первого порядка F(x, y, y’) = 0, перейдем к виду y’ = F(x, y).

Например,

(1) y’ + 3y= 0 с начальным условием y(0) = 4

переписывается в виде

(2) y’ =– 3y.

Для ОДУ второго порядка F(x, y, y’, y”) = 0 – к виду y” = F(x, y, y’).

Например:

(3) y”+y’+y–2x=0

с начальными условиями y(0) = 1; y’(0) = 3 переписывается в виде

y” = – y’ – y + 2x

и с помощью замены переменной z = y’ представляется в виде системы двух ОДУ первого порядка:

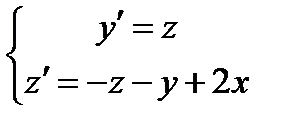
Для численного решения область непрерывного изменения аргумента х заменяют дискретным множеством точек, то есть вводят сетку. Независимая переменная берется в определенных точках (узлах) х₀, х₁, х₂, …, х_m, находящихся на расстоянии h друг от друга. Искомая функция ищется только в этих узлах, получают значения у₀, у₁, у₂, …, у_m. Она называется сеточной функцией.

Затем производные приближенно записывают через х₀, х₁, х₂, …, х_m, у₀, у₁, у₂, …, у_mи подставляют в исходное уравнение. В результате получаются уравнения для определения значений функции, в общем случае нелинейные. Такие методы счёта называются разностными схемами. При этом дифференциальные уравнения сводятся к алгебраическим, которые называются разностными уравнениями.

Схема называется устойчивой, если при малом изменении начальных (граничных) условий решение так же меняется мало.

Схема называется корректной, если решение существует и единственно при любых начальных (граничных) условия.

Схема явная, если для нахождения у_i требуется знать значения функции в предыдущих точках. В противном случае, схема является неявной.

⇐ Предыдущая12345Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: