Пример 3: Движение заряженных частиц в электрических и магнитных полях.

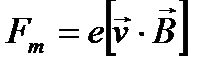В электрическом поле на частицу заряда e массой m действует электрическая сила . Где Е – напряженность электрического поля. В магнитном поле на частицу, движущуюся со скоростью v действует сила Лоренца , где В – индукция магнитного поля. Таким образом, уравнение движения частицы в электрических и магнитных полях в векторной форме имеет вид:

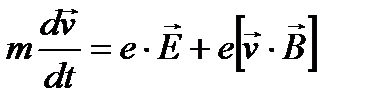
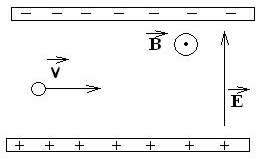
В случае скрещенных однородных стационарных полей, если вектор Е направлен по оси y, а вектор магнитной индукции В – по оси z, после замены переменных

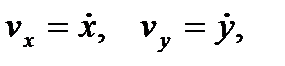
(х,у – координаты заряженной частицы), получается система уравнений:

Удобно решать эту систему ОДУ с начальными условиями

Разностная схема для метода Эйлера:

1. Движение в поле рассеивающего центра.

Движение заряженной частицы в неоднородном поле продемонстрируем на примере рассеяния. Рассмотрим частицу с зарядом e1, массой m, которая налетает на заряженный центр с зарядом e2, массы M >> m (см. рис.). На рисунке v0 – начальная скорость частицы, p – прицельное расстояние, θ – угол рассеяния.

Сила взаимодействия между частицей и центром находится по закону Кулона

,

где r – расстояние между центром и частицей. Если центр находится в точке с координатами (x0, y0), а (x,y) – координаты частицы, то проекции кулоновской силы

 

 

, , где .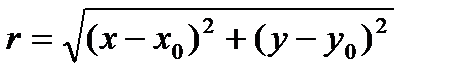

Удобно связать начало координат с рассеивающим центром, тогда x0=0,y0=0 и систему уравнений, описывающую движение заряженной частицы в данном случае можно записать в виде

и решать с начальными условиями x = - L, y = p, v_x = v, v_y = 0.

4. Механические колебания

Математический маятник (шарик на невесомой нити), выведенный из равновесия, может колебаться под действием возвращающей силы, величина которой, можно считать, пропорциональна отклонению от положения равновесия:

(20)

Здесь х – угол отклонения маятника от положения устойчивого равновесия, L – длина маятника, g – ускорение свободного падения.

Таким образом, колебания математического маятника без учета силы трения и при отсутствии вынуждающей силы описываются уравнением:

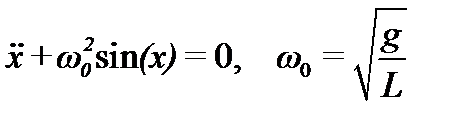(21)

Здесь ω₀ – собственная частота колебаний. Для решения уравнения второго порядка

(22)

Обозначим скорость маятника p=dx/dt и сведем ОДУ второго порядка к системе:

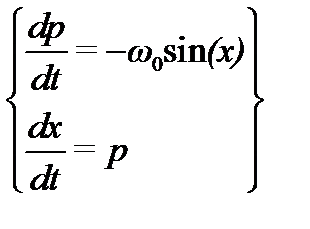(23),

которую можно решать с разными начальными условиями.

Для учета сопротивления воздуха в правую часть уравнения (20) добавляют слагаемое , при наличии периодической вынуждающей силы – слагаемое , где ω – частота вынуждающей силы.

Программа численного решения системы ОДУ (23) аналогична программе расчета характеристик движения тела в поле тяжести.

Запишем схему Эйлера, которая позволяет решать систему ОДУ численно:

(4)

Задачи

Механика

1.1. Шарик кидают с некоторой высоты H с начальной скоростью v₀. Рассчитать время падения шарика на землю численно без учета сопротивления воздуха и по формуле равноускоренного движения. Сравнить время падания при начальной скорости, направленной вверх, вниз и при свободном падении.

Построить зависимости его координаты и скорости от времени у(х) и v(х) при начальной скорости, направленной вверх, вниз и при свободном падении при различных значениях Н. Сопротивление воздуха не учитывать. Чем отличаются графики? Как по графику определить начальную скорость, координату?

Указание: Направить ось координат вверх. Н=0 соответствует поверхности земли.

 

1.2. Большой мяч массы M подбрасывают вверх с высоты H = Ho с начальной скоростью v₀. Рассчитать время его падения на землю с учетом сопротивления воздуха, пропорционального квадрату скорости (коэффициент сопротивления воздуха b = 0,05). Сравнить время его падания в воздухе со временем падения в вакууме.

Указание: Уравнение движения

Построить зависимость координаты мяча от времени при движении c учетом сопротивления воздуха, пропорционального скорости. Определить максимальную высоту подъема. Как высота подъема зависит от коэффициента сопротивления воздуха (постройте график)? Как время падения зависит от коэффициента сопротивления воздуха (постройте график)?

 

1.3. Камень массой 0,01 кг свободно падает с высоты Н. Экспериментально установлено, что сила сопротивления при этом пропорциональна квадрату скорости, коэффициент сопротивления для камня радиусом 0,01м равен b = 1E-4 кг/м. Из-за наличия сопротивления воздуха со временем скорость становится постоянной и равна примерно 30 м/с. Почему скорость становится постоянной? Рассчитать численное значение установившейся скорости, время и расстояние, после прохождения которого это происходит.

 

1.4. Построить зависимость от времени кинетической, потенциальной и полной механической энергии стального шарика, свободно падающего с высоты Н с учетом и без учета сопротивления воздуха. Какая часть механической энергии в последнем случае пойдет на нагревание? Если считать, что половина этой энергии уйдет на нагревание шара, на сколько изменится его температура? Шарик радиусом 0,01м, плотность стали ρ = 7,8 г/м3. Сила сопротивления F = b∙v^2, b = 1E-4 кг/м.

 

1.5. Построить траекторию движения тела, брошенного горизонтально с начальной скоростью v₀ без учета и с учетом сопротивления воздуха. Что это за кривая? Зависит ли время падения на землю от сопротивления воздуха? Какова зависимость горизонтальной скорости тела от времени? Бросают стальной шарик радиусом 0,01м, плотность стали ρ = 7,8 г/м³. Сила сопротивления F = b∙v², b = 10^-4 кг/м.

Какова зависимость горизонтальной скорости тела от времени без учета и с учетом сопротивления воздуха?

 

1.6. Построить траекторию движения тела, брошенного под углом α к горизонту с начальной скоростью v₀ без учета сопротивления воздуха. Численно и по формуле определить дальность полета L, высоту подъема Н и время подъема. Построить зависимость этих величин от угла α и найти угол, при котором тело имеет максимальную дальность полета.

 

1.7. Построить траекторию движения тела, брошенного под углом α к горизонту с начальной скоростью v₀ с учетом сопротивления воздуха. Как изменяется траектория при увеличении сопротивления воздуха? Как изменяется время и дальность полета в зависимости от угла α? Найти угол, при котором дальность полета будет максимальной. Как зависит результат от массы тела? Бросают деревянный, стальной, свинцовый шарики радиусом 0,01м. Плотность дерева – ρ = 0,7 г/м³, стали ρ = 7,8 г/м³, свинца ρ = 11,4 г/м³. Сила сопротивления F = b∙v², b = 10^-4 кг/м.

 

1.8. Шарик массой m= 2,2 г и радиусом r=4,1 мм падает в масле. Сопротивление вязкой жидкости F=6πrηv, где коэффициент вязкости жидкости η=0.96 кг/м∙с, v – скорость шарика. Найти зависимости ускорения, скорости, пути шарика от времени. Плотность масла ρ=0,9 г/м3

Указание: На шарик действуют силы тяжести, сопротивления жидкости, сила Архимеда.

Уравнение движения

1.9. Парашютист массой 70 кг совершает затяжной прыжок с высоты 7 км, свободно падая до раскрытия парашюта на высоте 500м. Найти зависимости ускорения, скорости, пути парашютиста от времени, если сила сопротивления воздуха F = A0∙v + B0∙v³, А0 = 5 Н∙с/м, В0 = 103 Н∙с³/м³. Становится ли при этом скорость постоянной? Через какое время? Какова ее величина? Сильно ли изменится результат, если в выражении для силы сопротивления F = A∙v + B∙v³ учесть зависимость коэффициентов от высоты A = A0∙exp(-m₀gh/RT) (для В – аналогично), где m₀ = 0,029 кг/моль –молярная масса воздуха, h-текущая высота, R = 8,31 Дж/(моль∙К), T = 273 К –температура.

 

⇐ Предыдущая12345Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: