 |
Моделирование физических явлений с помощью программы Calc.
|
|
|
|
1. Описание движения в поле тяжести с помощью обыкновенных дифференциальных уравнений
 Физические явления, рассматриваемые в данном курсе, обычно описываются одним или несколькими обыкновенными дифференциальными уравнениями (ОДУ).
Физические явления, рассматриваемые в данном курсе, обычно описываются одним или несколькими обыкновенными дифференциальными уравнениями (ОДУ).
Необходимо проанализировав условие задачи, записать систему ОДУ и дополнительные условия в соответствии с порядком уравнения и разрешить уравнения относительно старшей производной.
Рассмотрим движение тела, брошенного с начальной горизонтальной скоростью V0. Если не учитывать сопротивления воздуха, на такое тело действует только сила тяжести Fт=mg (см. рисунок). Уравнение движения тела получается из рассмотрения второго закона Ньютона:
 или
или  (1)
(1)
Выберем систему координат, начало отсчета которой, связано с землей, ось у направлена вверх. Тогда из (1) в проекциях на оси координат имеем:
 и
и  . (2)
. (2)
Начальные условия: при t = 0:
Для понижения порядка ОДУ вводим новые переменные и переходим к системе ОДУ первого порядка:
 (3)
(3)
Для решения задачи с использованием электронных таблиц воспользуемся определением производной через приращение функции:

Выразим искомые величины через бесконечно малое приращение времени dt.
Запишем схему Эйлера, которая позволяет решать систему ОДУ численно,:
 (4)
(4)
Где 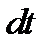 - шаг по времени. Значение индекса i определяет предыдущее значение функции, а i+1 последующее. Так как проекция ускорения на ось х равна нулю и скорость Vx не меняется, третье уравнение в системе (4) можно опустить. Учитывая начальные условия, получим
- шаг по времени. Значение индекса i определяет предыдущее значение функции, а i+1 последующее. Так как проекция ускорения на ось х равна нулю и скорость Vx не меняется, третье уравнение в системе (4) можно опустить. Учитывая начальные условия, получим
(5)
Таким образом, подставляя в схему Эйлера (4) начальные условия (5), можно получить значение координат и скоростей в момент времени t, а с их помощью – значения переменных в следующий момент времени и т.д.
|
|
|
Для учета сопротивления воздуха, во второй закон Ньютона (1) нужно включить еще одну силу
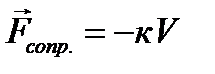 (6).
(6).
Тогда,
 (7).
(7).
Этот случай описывается следующей системой ОДУ первого порядка:
 (8)
(8)
Эта же система уравнений будет описывать и случай вертикального движения тела (только Vx = V0=0 и два первых уравнения в системе (8) можно не рассматривать), и случай движения тела с начальной скоростью, направленной под углом к горизонту.
Пример 1: Моделирование движения тела в поле тяжести
Задача: Тело брошено горизонтально со скоростью 2 м/с с высоты H = 50 м. Построить траекторию движения тела (зависимость Y от Х). На каком расстоянии от точки бросания тело упадет на землю?
Рассмотренная ниже последовательность действий показывает, как можно использовать редактор электронных таблиц для расчета значений функций 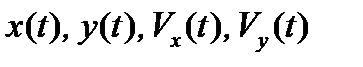 в соответствии с уравнениями схемы Эйлера (4), и построить траекторию движения тела.
в соответствии с уравнениями схемы Эйлера (4), и построить траекторию движения тела.
Последовательность действий:
1) Запустить табличный редактор O pen Office.Org. Calc.
2) В ячейках А1-Е1 подписываем заголовки столбцов таблицы t,  ;
;
3) В столбце А рассчитываем время. В ячейке А2 вводим 0 — начальное значение времени, а в ячейке А3 записываем формулу = А2 + 0,1, где 0,1 значение dt – шага времени.
4) Заполняем значения времени. Щелкаем на ячейке А3. Перемещаем курсор в правый нижний угол ячейки А3, пока курсор на превратится в знак «+», зажимаем левую кнопку мыши и протягиваем вниз, примерно до ячейки А37.
5) В столбце В рассчитываем координату х. В ячейки В2-Е2 записываем начальные условия (5), а в ячейку F2 значение шага по времени, в нашем примере 0,1. В ячейке G1 значение ускорения свободного падения g = 9,8.
6) В ячейке В3 набираем формулу = B2 + $F$2 * D2, где $F$2 – ссылка на ячейку F2, значение в которой не должно изменяться.
7) В столбце С рассчитываем координату у. В ячейке С3 аналогично записываем формулу: = C2 + $F$2 * E2
8) В столбце D рассчитываем горизонтальную составляющую скорости Vx. В ячейке D3 = D2 + $F$2 * 0
|
|
|
9) В столбце E рассчитываем вертикальную составляющую скорости Vy. В ячейке Е3 записываем формулу: = E2 - $F$2 * $G$2
10) Используя маркер автозаполнения «+», растягиваем значения ячеек В-Е последовательно до 37 строки включительно. Получаем таблицу значений.
При заполнении таблицы значений необходимо обратить внимание на значение координаты Y, которая не может быть < 0 (мы принимаем поверхность земли за нулевой уровень).
Для построения траектории движения тела необходимо выделить диапазон ячеек B2:С34. На панели задач выбрать пиктограмму диаграмма. В открывшемся окне мастера диаграмм, выбрать тип диаграммы <Диаграмма XY> и вид <линии и точки>. Нажимая последовательно кнопку <Далее>, подписываем название диаграммы и осей. Нажав кнопку готово, получаем траекторию движения тела, как показано на рис.

Из полученной зависимости мы делаем вывод, что тело упадет на землю на расстоянии приблизительно 6,5 м от точки бросания (координата Y =0).
Пример 2: Движение в поле тяготения
Движение тела массой m1 в поле тяготения массивного тела М происходит под действием гравитационной силы:
 (9)
(9)
Где  - радиус-вектор между взаимодействующими телами (направлен к m1),
- радиус-вектор между взаимодействующими телами (направлен к m1), -гравитационная постоянная. Будем считать, что M >> m1. Тело массой М в таком случае является неподвижным центром тяготения. Тогда уравнение движения тела массой m1:
 (10)
(10)
Совместим начало системы координат (0, 0) с центром масс массивного тела М. Тогда уравнение (10) в проекциях будет иметь вид:
 (11)
(11)
где x, y – координаты тела массой m1,  .
.
После замены переменных из (11) получается система ОДУ первого порядка:
 (12)
(12)
Для численного интегрирования этой системы записываем схему Эйлера:
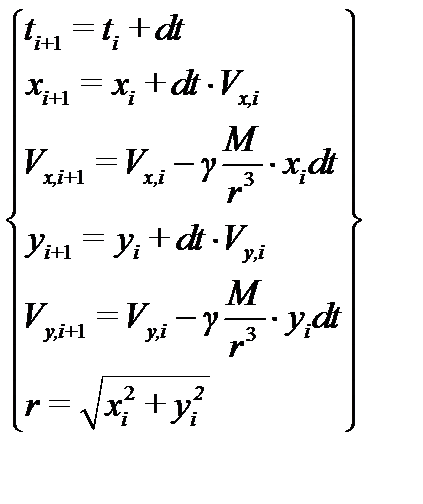 (13)
(13)
Удобно решать эту систему со следующими начальными условиями:
х(0) = х0; y(0) = y0 = 0; Vх(0) = Vх,0 = 0; Vy(0) = Vy,0 = V;
При этом тело массой m1 будет двигаться против часовой стрелки вокруг массивного тела М по эллипсу, оси которого будут параллельны осям координат.
Планеты Солнечной системы, движения которых моделируются в задачах, движутся с периодами, измеряющимися годами, по орбитам, оси которых измеряются миллионами километров. Таким образом, моделирование «в реальном времени» представляется неразумным. Разумные времена и размеры орбит получаются, если взять γ = 1, М = 1200, х(0) = 30, V~5.
|
|
|
Если в задаче рассматривается движение вокруг тяготеющего центра М двух невзаимодействующих планет с массами m1 и m2, уравнение движения, подобное (10), записывается для каждого тела:
 (14)
(14)
Если учитывать взаимодействие планет с массами m1 и m2 не только с Солнцем, но и друг с другом, необходимо учесть гравитационные силы взаимодействия между ними (см. рисунок). На первую планету со стороны второй действует сила:
 (15)
(15)
Вектор  имеет координаты и длину
имеет координаты и длину
 (16)
(16)
Проекции силы  на оси координат
на оси координат
 (17)
(17)
На вторую планету со стороны первой действует сила . По третьему закону Ньютона:
 (18)
(18)
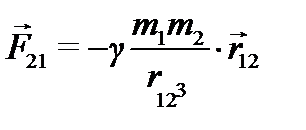 (19)
(19)
Результат моделирования движения планет показан на рис.

|
|
|


