Аналого-цифровое преобразование сигналов

Аналого-цифровым преобразованием (АЦП) называют узел, однозначно преобразующий значение непрерывной аналоговой величины в цифровую (дискретную).

Преобразование осуществляется в течение определенного временного интервала T, а результат представляется в виде кодовых комбинаций параллельного и, реже, последовательного цифрового кода. Наиболее часто используется двоичный и двоично-десятичный код. Преобразователи аналог – код цифра широко применяются в измерительной и телеизмерительной технике, в области связи, телевиденье и др.

Существует множество методов преобразования непрерывной величины в цифровой код, которые могут быть разделены по принципу действия на четыре метода:

1. время–импульсный;

2. частотно–импульсный;

3. кодо–импульсный (следящего уравновешивание);

4. пространственного кодирования (или шифраторы перемещения).

Одним из основных требований, предъявленных к АЦП, является возможность восстановления непрерывного сигнала путем формирования воспроизводящей функции y(t) по ее координатам. Для этой цели могут использоваться временные ряды Котельникова или алгебраические полиномы. Как известно, В.А.Котельников показал, что если функция x(t) ограничена высшей гармоникой F_{u max}, то она может быть с любой степенью точности восстановлена по ординатам, взятым через отрезки времени:

 

путем суммирования членов бесконечного ряда:

 

где k – порядковый номер ординаты.

Однако, практическое применение теоремы Котельникова связано с рядом трудностей и в общем позволяет получить предельные значения шага квантования по времени.

При решении практических задач более приемлемо использование для формирования воспроизводящей функции y(t) сменных многочленов Лагранжа.

Для осуществления АЦП необходимо в первую очередь выбрать значение шага дискретизации по времени ∆t и шага квантования по уровню ∆x из условия получения допустимой погрешности преобразования.

Погрешность воспроизведения исходной непрерывной функции x(t) с ограниченными производными многочленами Лагранжа определяется остаточным членом:

 

здесь – модуль максимального значения (n +1) производной функции x(t);

n – степень аппроксимирующего многочлена.

ti-1

t

ti

ti+1

∆t

x(t)

y(t)

∆xm

 

 

Рис.5.22. Ступенчатая аппроксимация непрерывной функции x(t)

 

Так, при использовании многочлена нулевой степени (ступенчатая аппроксимация) величина шага ∆t определяется в предположении, что за шаг дискриминации разность у(t) – x(t) не превысит наперед заданного значения.

При этом n = 0 и

 

Если считать, что:

 

то

 

Если задается значение относительной приведенной погрешности, то

 

– максимальное значение функции;

– максимальное значение первой производной x_m (можно найти графическим дифференцированием характерного участка y(t)).

Если ступенчатая аппроксимация приводит к недопустимо малым значением ∆t, то следует применить линейную аппроксимацию (n = 1). При этом:

 

 

При этом значение шага дискретизации оказывается равным:

 

 

Максимальное значение второй производной можно найти двойным графическим дифференцированием характерного участка y(t) (на котором 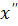– максимально).

Аналогичный подход применяется при определении числа уровней квантования. Обычно

 

 

где δ – допустимая относительная погрешность.

Система основных электрических параметров АЦП, отражающая особенности их построения и функционирования, включает:

- число разрядов b – число разрядов кода, связанного с аналоговой величиной, которое может вырабатывать АЦП;

- коэффициент преобразования К_пр – отношение приращения выходного сигнала к приращению входного для линейной характеристики;

- абсолютную погрешность преобразования в конечной точке шкалы δ_nш;

- напряжение смещения нуля на входе U_вх0 (в единицах младшего разряда);

- время преобразования t_пр.

 

5.3.1. Время-импульсные АЦП

 

Основой метода время-импульсного преобразования является предварительное линейное преобразование измеряемой аналоговой величины во временной интервал и непосредственное кодирование временного интервала.

tx

t0

T0

t

t

t

t

Ux

Ux

Tx

Tx

····························· ··

·····························

 

 

Рис.5.23. Временные диаграммы метода линейной аппроксимации

 

Временные диаграммы иллюстрируют метод линейной аппроксимации, здесь:

U_x – мгновенное значение измеряемой величины;

T_x – временной интервал, пропорциональный U_x;

T₀ – длительность шага дискретизации.

Мгновенное значение измеряемой величины U_x подается на вход УС и преобразуется в пропорциональный этому значению интервал времени T_x:

 

Сброс

Ux

Код

CT

И

G1

FR

G11

S R

T

G12

УС

G2

Запись

 

 

Рис.5.24. Блок-схема преобразования напряжения в код

(G₂ – ГЛИН, Т – RS триггер, УС – компаратор, G1 – одновибраторы)

 

Эти пять узлов осуществляют преобразование измеряемой величины U_x во временной интервал T_x следующим образом. Генератор сигналов образцовой частоты G₁ генерирует сигналы прямоугольной формы высокостабильной частоты f₀, которые через логический элемент И поступают на вход счетчика импульсов CT в течение временного интервала T_x.

Делитель частоты FR играет вспомогательную роль: фронт прямоугольного импульса очищает разряды счетчика CT, переводит триггер T подачей на прямой вход импульса одновибратора G1₁ в открытое состояние и запускаем генератор линейно-изменяющегося напряжения G₂. Напряжение с выхода ГЛИН поступает на второй вход устройства сравнение (компаратора). Срез импульса запирает ГЛИН и дает команду на запись кода из разрядов счетчика в регистры памяти или передачу в шифратор.

Очевидно, число импульсов N, прошедших в счетчик, пропорционально временному интервалу T_x

 

 

а, следовательно, и измеряемой величине Ux.

Следует отметить, что включение генератора импульсов стабильной частоты в течение интервала T_x является простейшим видом кодирования с использованием последовательного число-импульсного кода, а включение счетчика этих импульсов – перекодирование в двоичную, двоично-десятичную или другую систему счисления. На счетчике производится запоминание кодовой комбинации т.е. представление измеряемого значения в параллельном коде. Преобразование в последовательный код для передачи по каналу связи осуществляется считыванием информации со счетчика с определенной скоростью. При этом минимальное время запаздывания

 

 

где T_сч – время считывания кодовой комбинации со счетчика.

Выбор времени считывания T_сч определяется полосой пропускания канала связи:

 

 

где n – число разрядов кода;

∆f – полоса пропускания канала связи.

Время-импульсное преобразование получило также название развертывающего преобразования, к разновидностям которого относится преобразование со ступенчатой формой нарастающего напряжения. В этом случае ГЛИН заменяется генератором ступенчато-возрастающего напряжения.

∆Uкв

Tx

t

Ux

U

 

 

Рис.5.25. Метод время-импульсной дискретизации

непрерывной функции U(t)

 

Относительная погрешность при этом равна шагу квантования∆U_кв.

Метод время-импульсного преобразования позволяет создавать наиболее точные АЦП аналог-цифра с электрическим входом, но с низким быстродействием. Они широко используются на передающей стороне в кодо-импульснных устройствах телеизмерения.

 

5.3.2. АЦП следящего уравновешивания

 

Метод следящего уравновешивания заключается в поочередном сравнении измеряемой величины с эталонной дискретной. Эта величина образуется в процессе сравнения как сумма коэффициентов соответствующего цифрового кода.

Для двоичного кода:

 

где ∆U_кв – вес кванта;

K_i = 1,0 – коэффициенты двоичного кода;

m = 2 – основание кода;

i – число разрядов кода, определяющее число сравнений.

Состояние соответствующего разряда кода определяется результатом логического сравнения (>; <; =) меры и измеряемой величины.

Например.

Измеряемая величина U = 53V.

Число разрядов кода n = 6.

2⁵ 2⁴ 2³ 2² 2¹ 2⁰ – Вес разряда в двоичной коде.

32 16 8 4 2 1 – Вес разрядов в десятичном коде.

1 1 0 1 0 1 – Результат сравнения.

Вес одного кванта ∆U = 1V.

Предел измерения U_max = 2ⁿ = 2⁶ = 64.

Число разрядов кода n = 6 определяет число шагов приближения к измеряемому значению.

U

U=25+24<Ux

U=25+24+23-22+21-20=Ux

U=25+24+23-22+21

U=25+24+23>Ux

20

21

22

23

24

25

Вес кода

 

 

Рис.5.26. Метод следящего уравновешивания

 

Первоначально сравнение осуществляется со старшим разрядом

U_x ~ 2⁵ 2⁵ < U_x → 1; (5.30)

 

по результату логического сравнения (U < U_x) первому разряду присваивается 1. Так как U < U_x вес следующего разряда прибавляется к U

U = 2⁵ + 2⁴ < U_x → 1. (5.31)

 

Следующему разряду также присваивается 1 по результату логического сравнения.

Затем

U = 2⁵ + 2⁴ + 2³ > U_x → 0 (5.32)

 

Третьему разряду присваивается 0 по результату сравнения U > U_x.

Следующий разряд берется со знаком минус

U=2⁵+2⁴+2³-2² < U_x→ 1 и т.д. (5.33)

 

Получили код 110101 = 54.

Процесс сравнения продолжается до равновесия с максимальной абсолютной погрешностью.

В АЦП последовательных приближений (следящего уравновешивания) используется, как правило, ЦАП в цепи обратной связи. Структурная схема такого АЦП может иметь вид:

Ux

СО

ЦАП

УУ

ГТИ

ПК

 

Рис.5.27. Структурная схема АЦП

 

Измеряемое напряжение U_x сравнивается в компараторе СО с мерой, образуемой при каждом такте задающего генератора ГТИ в устройстве управления УУ и преобразуемое в аналоговую форму в ЦАП. При уравновешивании до максимальной погрешности:

 

подается команда на передачу двоичного кода в преобразователь кодов – ПК (шифратор) и затем – в канал связи.

Выпускаются серийно ЦАП следящего уравновешивания с высоким быстродействием – частота тактов выше 1 MHz – в интегральном исполнении.

Одним из наиболее совершенных типов АЦП является интегрирующий последовательного счета. Они делятся на АЦП с двухтактным интегрированием и АЦП с дискретной обратной связью. Первые бывают с интегрированием входной величины за постоянный интервал времени и АЦП с интегрированием входной величины до заданного уровня. Принцип их действия состоит в том, что в первом такте интегрируется входной сигнал, а во втором – противоположный ему по знаку сигнал от опорного источника.

В интегрирующих АЦП с дискретной обратной связью измерение входного сигнала и счет импульсов генератора осуществляются одновременно. На входе интегратора происходит управляемый процесс суммирования или вычитания эталонных токов, поддерживающих выходное напряжение генератора, равным опорному. Число импульсов в счетчике пропорционально входному сигналу.

5.3.3. АЦП пространственного кодирования

 

Метод пространственного кодирования основан на предварительном преобразовании измеряемой величины в пропорциональное угловое или линейное перемещение кодирующей линейки (маски) относительно считывающего устройства. Перемещению, равному

 

где ∆l_кв – перемещение на один шаг квантования,

соответствует кодовая комбинация, отображающая число K:

 

Кодовая комбинация, определяемая данным положением маски, вырабатывается в процессе считывания информации с кодовой маски.

Пример кодирующей маски 5-ти разрядного натурального двоичного кода:

24

∆l

10101=21

23

22

21

20

 

 

Рис.5.28. Кодирующая маска 5-ти разрядного кода

 

Структурная схема АЦП пространственного кодирования с кодирующим диском имеет вид:

αx

ФД3

Ш

МУ

ПК

ФД5

ФД4

ФД2

БФ

ФД1

 

Рис.5.29. Структурная схема АЦП пространственного кодирования

с кодирующим диском

 

Осветитель, число ламп которого равно числу разрядов кодирующей маски, создает световой поток Ф, который через щелевые диафрагмы попадает на кодирующий диск, который является входным элементом.

Разрешающая способность преобразования (шаг квантования по уровню) определяется углом θ

 

где n – число разрядов двоичного кода (n = 5). Все секторы пронумерованы числами 0, 1, 2, 3, …, i, …, n-1. Запись каждого сектора (его номер) в каком либо двоичном коде отображена в пределах соответствующего сектора комбинацией прозрачных и непрозрачных участков. Единицы закодированы непрозрачными участками, а нули – прозрачными.

Считывание значения угла поворота диска (либо линейного перемещения маски) производится с помощью отсчетного устройства. Лучи света попадают на блок фотодатчиков БФ. По состояниям фотодатчиков ФД1…ФД5 на выходах блока формирователей БФ появляются сигналы, кодирующие номер сектора диска в одном из двоичных кодов. Как правило, используются рефлексные коды (например, код Грея). У рефлексных кодов соседние сектора могут отличаться не более чем на один разряд. Поэтому ошибка считывания не превысит θ.

Затем рефлексный код преобразуется в двоичный натуральный в преобразователе кода ПК.

Результат преобразования умножается на θ в множительном устройстве

где i – номер сектора.

Затем двоичный код α_x преобразуется в шифраторе в циклический с соответствующим уровнем защиты от ошибок при передаче и передается по каналу связи.

5.3.4. Частотно-импульсные АЦП

 

Суть метода заключается в предварительном преобразовании измеряемого параметра X в пропорциональную ему частоту

 

и счете числа периодов этой частоты счетчиком соответствующей системы счисления за строго фиксированный временной интервал T₀. Минимальное время запаздывания T_3minпри передаче кодовых комбинаций частотно-импульсным методом преобразования

 

где T_сч – время считывания кодовой комбинации.

Величина T₀ определяет погрешность преобразования, равную

 

x

УУ

ДИВ

СЧ

Кл

ГУ

 

Рис.5.30. Структурная схема частотно-импульсного преобразователя

(ГУ – генератор регулируемой частоты; Кл – ключ;

СЧ – счетчик импульсов; ДИВ – датчик интервалов времени;

УУ – устройство управления)

 

Измеряемая величина Х преобразуется в пропорциональную ей частоту f = k·x в управляемом генераторе ГУ. Устройство управления УУ подает команду на выключение ключа Кл в течении фиксированного интервала времени T₀, определяемом датчиком интервалов времени ДИВ. Сигналы с частотой f = k·x проходят на счетчик.

В телеметрических системах с узкополосными каналами связи необходимо выбирать сравнительно низкие частоты. При этом получаются сравнительно длительные интервалы измерения T₀ ≥ 5s, что не удовлетворяет требованиям по быстродействию.

Метод пространственного кодирования широко применяется в радиолокации, в военной технике для получения данных об угловых координатах целей или средств поражения непосредственно в цифровой форме.

Технические средства пространственного кодирования используются также и при нелинейной зависимости перемещения и измеряемого параметра.

 

5.3.5. Цифро-аналоговые преобразователи

 

Цифро-аналоговые преобразователи (ЦАП), предназначены для преобразования цифровых сигналов в аналоговые и служат для сопряжения цифровых устройств формирования и обработки сигналов с аналоговыми потребителями информации. ЦАП является обратным преобразователем АЦП. Они широко применяются в следующих отраслях техники:

- системы управления технологическими процессами;

- устройства связи, телемеханики, телеметрии;

- дискретная автоматика и вычислительная техника;

- испытательная и измерительная техника.

ЦАП могут быть построены с большим быстродействием и меньшей погрешностью.

ЦАП способны работать с различными видами входных цифровых кодов: двоичным, дополнительным, Грея, двоично-десятичным и др. Наиболее широко распространены преобразователи с двухпозиционным параллельным кодом.

К простейшим и наиболее широко применяемым в электронике и телеметрии ЦАП относятся преобразователь цифровой код-сопротивление резистора. Схема такого преобразователя для n-разрядного двоичного кода имеет вид:

 

2n-1·R0

22·R0

21·R0

20·R0

Выход

 

 

Рис.5.31. Схема ЦАП цифровой код – сопротивление резистора

 

≫

Если такую схему включить последовательно со стабилизированным источником тока J(), то получаем преобразователь цифра-напряжение, а последовательно с источником напряжения – цифра – ток. Электронные ключи управляются содержанием соответствующего разряда кода. При этом, если a_i = 1, то ключ размыкается и наоборот при a_i = 0 – ключ замыкается.

Уравнение ЦАП с последовательно включенными резисторами для двоичного натурального кода такое:

 

 

Здесь R₀ – сопротивление резистора, равное шагу квантования.

Для схемы с параллельно включенными резисторами выходная проводимость для двоичного натурального кода будет:

 

 

K i = 0

K = 2

K = 1

Выход

K i

 

 

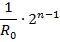
Рис.5.32. Структурная схема ЦАП с параллельно включенными

резисторами

 

Параллельное включение реализуется более просто с бесконтактными ключами.

В связи с трудностями создания идеальных источников тока и напряжения применяются преобразователи цифра-напряжение с суммированием токов отдельных секций на выходном резисторе R_вых.

 

 

При этом необходимо выполнение условия R_i ≫ R_вых.

Rn

E

Uвых

Rвых

R2

R1

 

 

Рис.5.33. Структурная схема ЦАП с суммированием токов

отдельных секций

 

Весовые коэффициенты резисторов a ₀, a ₁, a ₂, … a _n-1 пропорциональны проводимостям соответствующих разрядов. В ЦАП высокого класса точности (δ < 0,1%) применяют контактные ключи вместо электронных т.к. у последних недостаточно большое отношение:

 

Суммарная приведенная погрешность ЦАП равна:

 

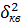– погрешность квантования;

– погрешность от нестабильности R;

– погрешность, обусловленная нестабильностью ключей (превалирует над другими);

– погрешность источников питания при постоянной нагрузке;

– то же, но при изменении нагрузки.

С целью уменьшения влияния нестабильности сопротивлений резисторов применяют схемы ЦАП с резистивными сетками типа R – 2R, в которых сопротивление нагрузки источника питания остается практически неизменным при переключении ключей. Кроме того, выполнение такой сетки требует только двух номиналов сопротивлений R и 2R.

2R

a n

a 6

a 5

a 4

a 3

a 2

a 1

Uвых

2R

R

R

R

2R

R

2R

R

2R

R

2R

2R

2R

U0

 

 

Рис.5.34. Схема ЦАП с резистивными сетками типа R – 2R для двоичного натурального семиразрядного кода

 

Ключ старшего разряда расположен справа.

Резистивные цепи типа R – 2R выполняются в виде интегральных микросхем (серии 252, 265, 301).

Для повышения быстродействия сеточных ЦАП применяют схемы на ОУ с суммированием токов.

Микросхема ЦАП К5762ПА1 является 10-ти разрядным универсальным звеном для построения микроэлектронных ЦАП, АЦП и управляемых кодом делителей тока. Она выполнена по МОП – технологии на одном кристалле. В состав кристалла входит традиционная резисторная матрица типа R – 2R, токовые ключи на МОП – транзисторах и входные усилители-инверторы. Микросхема работает с прямым параллельным двоичным кодом.

 

 

⇐ Предыдущая10111213141516171819Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: