 |
Проектирование цифровых устройств
|
|
|
|
Комбинационные и последовательностные цифровые устройства
У комбинационной логической схемы (или линейной схемы автомата без памяти) состояние выходов схемы определяется только комбинацией входных логических сигналов. Для последовательностного автомата состояние его выходов определяется последовательностью поступления входных сигналов, при этом предшествующие комбинации входных сигналов фиксируются в памяти автомата изменением его внутренних состояний. Таким образом последовательностный автомат - это комбинационный автомат с памятью.
Автоматом – называют устройство, выполняющее определенный процесс без непосредственного участия человека. Последовательностный автомат с конечным числом функционально-различимых внутренних состояний, входов и выходов называют конечным автоматом.
Рис.6.1. Обобщенная схема последовательностного автомата
6.1.1. Машина Тьюринга
Все реально существующие автоматы являются конечными. Бесконечный автомат - это абстрактное понятие, введенное как инструмент изучения последовательностных цифровых логических схем. Примером бесконечного автомата является машина Тьюринга. Она имеет следующие составные части (рисунок 92):
- входную бесконечную ленту L1 с памятью, разделенную на ячейки от X0 до Xn, где n = ¥;
- выходную бесконечную ленту L2 с памятью, разделенную на ячейки от Y0 до Yn, где n = ¥;
- управляющее устройство УУ.
Обе ленты могут свободно произвольно продвигаться в обоих направлениях и таким образом к УУ может быть подключено бесконечное (¥) число входных и выходных комбинаций (состояний).
Рис.6.2. Машина Тьюринга
Любой конечный автомат можно рассмотреть как частный случай Машины Тьюринга. Различают асинхронные и синхронные автоматы.
|
|
|
1) Асинхронные (нетактируемые) – изменение состояния их выходов происходит непосредственно вслед за изменением входных сигналов.
2) Синхронные (тактируемые) – входные сигналы изменяют состояние выходов автоматов лишь при наличии синхронизирующего (тактового) сигнала, при его отсутствии и изменении входных сигналов выходные сигналы будут оставаться неизменными (предыдущими). В теории конечных автоматов различают автоматы Мили и Мура.
Автомат Мура – это конечный автомат с памятью, состояние выходов которого определяется только его внутренним состоянием памяти.
Автомат Мили – это конечный автомат с памятью, состояние выходов которого определяется одновременно и входными сигналами и внутренним состоянием памяти.
6.1.2. Способы описания последовательностных конечных автоматов
В настоящее время сложилась некоторая определенная иерархия языков описания алгоритмов функционирования конечных автоматов, а именно: первичные, базовые, автоматные, выходные.
1) Первичные - языки, наиболее приближенные к естественному языку разработчика (например словесный алгоритм функционирования);
2) Базовые - позволяют сразу описывать условия работы автомата (например, графические и логические схемы алгоритмов);
3) Автоматные - это абстрагированные языки, предназначенные для преобразования и оптимизации автоматов (к ним относят графы, таблицы переходов, переключательные функции);
4) Выходные языки - ориентированы на получение такой формы представления информации, которая наиболее удобна для реализации схемы автомата на конкретных функциональных элементах (например на вентилях «И - НЕ»). К выходным языкам относят, в частности, таблицы состояний, преобразованные переключательные функции булевой алгебры.
К способам описания конечных автоматов относят также: матрицы соединений, логические сети, циклограммы, таблицы переходов и другие.
|
|
|
Булева алгебра
Этот математический аппарат был предложен в конце девятнадцатого века французским психологом Джорджем Булем для исследования логики человеческого мышления. Поэтому, кроме как по имени автора - алгебра Буля или Булева алгебра, его ещё называют алгеброй логики. Сегодня - это инструмент описания работы электронных логических схем. Логическими переменными в булевой алгебре являются логические величины «1» или «0» («Да» или «Нет»), («Истина» или «Фальш»). Такие переменные назвали двоичными, так как они могут принимать только два значения.
Основными действиями над двоичными переменными в булевой алгебре являются:
· логическое сложение – дизъюнкция (обозначается символами V; +; ИЛИ);
· логическое умножение – конъюнкция (обозначается символами L; ·; И);
· логическое отрицание – инверсия (обозначается символом НЕ; горизонтальной чертой над символом переменной).
Логические функции, записанные с помощью элементарных действий булевой алгебры часто называют также переключательными, поскольку ранее они реализовывались на механических переключателях, либо на контактах электромагнитных реле.
6.2.1. Основные законы Булевой алгебры
Базовые элементарные логические функции булевой алгебры и их возможные преобразования представлены в таблице. Здесь же показаны соответствующие логическим функциям эквивалентные контактные схемы. В таблице замкнутому состоянию контактов соответствует логическая «1», разомкнутому - логический «0». Нормально-разомкнутый контакт имеет обозначение без инверсии, а нормально-замкнутый - с инверсией; буквой А – обозначена логическая переменная; цифрой 1 - обозначена логическая константа.
Таблица 6.1.
Основные законы булевой алгебры и их эквивалентные схемы
| № | функция | Эквивалентная контактная схема |
 1
|
| 
|
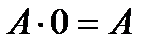
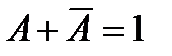
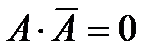
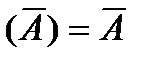
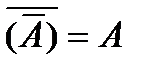
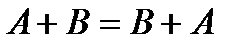
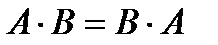
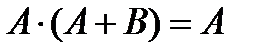
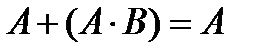
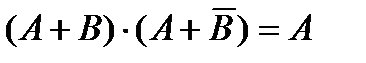
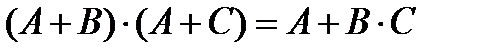
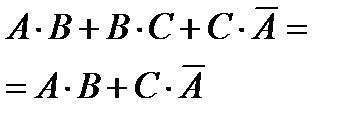
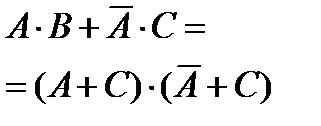
Таблица 6.2.
|
|
|
Переключательные функции основных законов алгебры логики
1.Переместительный закон.
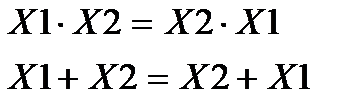2. Сочетательный закон.
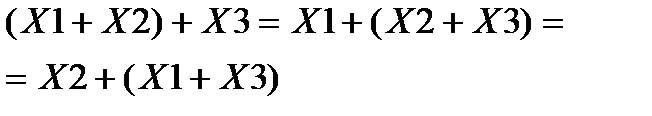3. Распределительный закон.
|
4. Закон инверсии
(правило Моргана-Шеннона).
5. Закон склеивания.
6. Закон поглощения.
|
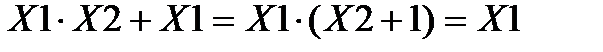
6.2.2. Функционально-полный базис
Логическую функцию любой сложности можно представить как комбинацию трёх основных действий булевой алгебры - сложения, умножения, отрицания. Набор этих элементарных функций называется функционально-полным. Логические элементы, реализующие три основные логические функции, образуют функционально-полный элементный базис. Это означает, что с помощью трёх основных функций можно записать любую логическую функцию, а на основе функционально-полного базиса - её реализовать. Например, для осуществления вычитания можно использовать логическое сложение одной переменной с дополнительным кодом другой переменной.
Функционально-полными являются также и другие комбинации основных логических функций. Например для ТТЛ-микросхем серии К155 (зарубежный аналог - серия SN74) функционально-полными является базис логического вентиля «И-НЕ».
|
|
|
