Особенности представления цифровых сигналов

 

Дискретные электронные устройства в настоящее время очень широко используются в технике. Это объясняется их преимуществами по сравнению с аналоговыми (непрерывными во времени носителями информации). Своим развитием дискретные системы обязаны в первую очередь изобретению цифровых вычислительных машин. Затем на основании разработанной теории и технологии дискретные и в первую очередь цифровые электронные системы начали уверенно вытиснять аналоговые системы, значение последних, однако, остается весьма высоким.

Особенностью цифровых сигналов и схем является то, что описывающими их параметрами являются не конкретные значения токов и напряжений, а абстрактные символы 0 и 1 (истинно – ложно и т.д.), которыми представляются как входные, так и выходные сигналы цифровых устройств.

Эта особенность цифровых устройств потребовала разработки специального математического аппарата.

Следует отметить, что значение двоичных сигналов 0 и 1 не дают никакой количественной оценки состояний цифровых элементов. Однако в вычислительной технике, автоматике, телеметрии, и некоторых других технических направлениях, использующих двоичные системы счисления, их можно рассматривать как цифры этой системы счисления.

В двоичной системе счисления число A можно представить в виде суммы:

A = a_n-12^n-1 + a_n-22^n-2 +…+ a_i2ⁱ +…+ a₀2⁰ + a_-12^-1 + a_-22^-2 +…+ a_-m2^-m =

 

Например, десятичное число 29,32 запишется так:

29,32 = 11101, 0101001. (5.14)

 

Как видно, в двоичной системе число разрядов существенно больше для одного и того же числа.

Математическим аппаратом для функции и аргументов, могущих принимать только два значения – 0 и 1, является булева (двоичная) алгебра логики.

Логическими переменными в двоичной алгебре называются величины, которые независимо от их конкретного физического смысл, могут принимать только два значения – 0 и 1.

Логические переменные в булевой алгебре обозначаются, как и в обычной алгебре, буквами латинского алфавита с индексами (Х₀, Х₁, Х₂, Х₃, …), причем, если Х_n = 1, то переменная так и обозначается X_n, при X_n = 0, она обозначается так _n. Так, в двоичном коде число 01001 обозначается так ₄, ₃, ₂, ₁, ₀. Логические или переключательные функции, так же как и их переменные, могут принимать только два значения – 0 и 1. Логические функции называются полностью определенными, если указаны значения для всех наборов их аргументов.

Булевы функции бывают комбинационными и временными (последовательными).

Существуют различные способы задания или представления логических функций:

1. словесное представление;

2. табличный способ;

3. аналитический способ;

4. числовой способ.

Аналитический способ задания логических функций заключается в том, что логическая функция F задается в виде алгебраического уравнения, в котором переменные аргументы X_i связаны между собой знаками логических операций:

Ù, & – логическое умножение (конъюнкция);

+, Ú – логическое сложение (дизъюнкция);

≡ – равнозначность;

– отрицание;

Å – неравнозначность.

Аналитическая форма записи функции позволяет сформулировать основные законы алгебры логики, которые записываются отдельно для операций ИЛИ и И:

Таблица 5.1.

Основные законы алгебры логики.

Дизъюнктивная форма	Конъюнктивная форма
1. Законы нулевого множества
2. Законы универсального множества
3. Законы повторения
4. Закон двойного отрицания
т.е. двойную инверсию можно снять.
5. Закон отрицания
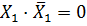
6. Переместительный закон (коммутативности)
7. Сочетательный закон (ассоциативности)
8. Распределительный закон (дистрибутивности)
9. Закон поглощения
10. Закон склеивания (распространения)
11. Правило де Моргана

Истинность приведенных законов может быть доказана подстановкой всех комбинаций перемененных X_i или путем алгебраических преобразований.

Применение этих законов позволяет упростить логические функции.

Используя законы ассоциативности (сочетательные), можно любую логическую функцию многих переменных представить в виде комбинаций функций двух переменных.

Полный набор 2²²= 16 логических функций двух переменных представлен в таблице 2.

Любая логическая функция из полного набора двух переменных может быть образована (выражена) посредством только трех логических элементарных функций: И, ИЛИ, НЕ.

Числовой способ задания функций используется для сокращения ее записи, при этом переключательная функция записывается в виде логической суммы десятичных номеров двоичных наборов, на которых функция равна единице

 

для функции, приведенной в ниже следующей таблице 5.3.

При табличном способе логическая функция задается в виде таблицы соответствия (таблицы истинности), устанавливающей связь между всеми возможными наборами аргументов (входных величин) и значениями функции. Число наборов аргументов, а следовательно и число значений функции, равно 2ⁿ, где n-число переменных (аргументов).

Например: функция F(X_n) может быть описана словесно – функция трех аргументов принимает значения единицы, если два и более ее аргументов равны единице. При n = 3 число наборов 2³ = 8.

Областью определения этой булевой функции трех аргументов является совокупность 2ⁿ = 2³ = 8 наборов.

В булевой алгебре особое место занимают функции двух переменных. Располагая набором функций двух переменных, на основании принципа суперпозиции (наложения) можно образовать переключательную функцию любого числа переменных.

В приведенном выше полном наборе 16 логических функций двух аргументов внизу приведены четыре возможных набора аргументов, а выше – значение шестнадцати различных элементарных функций, их названия. Эти функции неэквивалентны по значимости, широте применения и технической реализации.

Наиболее широко используются функции И(1); ИЛИ(7); HE(10, 12); ИЛИ-НЕ(8); И-НЕ(14). С их помощью можно задать любую другую функцию, они универсальны, для них наиболее полно разработан матаппарат.

 

Таблица 5.2.

Полный набор двоичных логических функций двух переменных

0.			Константа 0.
1.			Конъюнкция (И) X1, ÙX2 (умножения)
2.			Запрет по Х2, запрет
3.			Тождественность Х1, переменная Х1
4.			Запрет по Х1, запрет
5.			Тождественность Х2, переменная Х2
6.			Неравнозначность, сумма по mod2, исключающее ИЛИ
7.			Дизъюнкция, ИЛИ, логическое сложение
8.			Отрицание дизъюнкции стрелка, Пирса, ИЛИ- НЕ
9.			Равнозначность, эквивалентность X1 ≡ X2
10.			Отрицание , инверсия X2
11.			Импликация по Х2, Х2 → Х1, Х1 + ,
12.			Отрицание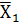
13.			Импликация по Х1, Х1 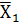→ Х2, +Х2
14.			Отрицание конъюнкции, штрих Шеффера, И-НЕ, Х1 Х2
15.			Константа единицы

X₁ 0011

X₂ 0101

 

истинность

 

Таблица 5.3.

Таблица истинности двоичной логической

функции трех переменных

№ набора	Аргументы	Функция F
Х1	Х2	Х3

 

 

5.2.1. Основы анализа логических схем

 

Основной задачей синтеза (построения) логической схемы является отыскание ее структуры, удовлетворяющей выбранному критерию оценки качества. Структурные схемы, получаемые из задания логических функций в неявном виде одним из способов, еще не являются реальными схемами, как правило, являются избыточными и могут быть существенно упрощены посредством ряда формальных операций, называемых минимизацией. Целью минимизации является получение логической схемы, содержащей минимальное число логических элементов с минимальным числом входов.

Наиболее эффективными операциями минимизации является применение законов склеивания и поглощения. Способов минимизации логических функций существует достаточно много и отличаются они в основном поиском соседних конъюнкций ().

Наиболее распространены способы с применением карт Вейча и Карно.

Следует отметить, что в настоящее время задача, минимизации структуры логических функций в значительной мере потеряла свою актуальность. Это связано с серийным выпуском интегральных логических микросхем, реализующих логические функции широкого класса.

 

5.2.2. Логические элементы

 

Для реализации функций алгебры логики используются такие логические элементы:

 

1. Конъюнктор (элемент И) – двоичный логический элемент, реализующий операцию “логическое умножение”, у этого элемента уровень логической единицы на выходе будет только в том случае, если на всех входах будет уровень “1” одновременно.

 

Xn

X2

X1

Y

&

X1, X2, … Xn – входы. Y – выход.

 

 

Рис.5.14. Условное обозначение логического элемента И.

 

X1

t

U1

U0

t

U0

U1

X2

t

U0

U1

X3

t

U0

U1

y

 

Рис.5.15. Временные диаграммы трехвходового логического элемента И

 

Таблица 5.4.

R1

X1

X2

Сn

y

X3

Таблица истинности трехвходового

логического элемента И

Х1 Х2 Х3 Y

 

 

Рис.5.16. Схема электрическая

трехвходового логического элемента И

 

В сериях К172, К178, К155 элементы И на МДП – транзисторах (полевых) с отрицательным источником питания.

2. Дизъюнктор (элементы ИЛИ) – двоичный логический элемент, реализующий операцию “логическое сложение”, уровень логической единицы на выходе которого имеет место, если хотя бы на одном входе имеется высокий уровень единицы.

Xn

X2

X1

Y

Логическое уравнение работы дизъюнктора Y = X1 + X2 + X3

 

Рис.5.17. Условное обозначение логического элемента ИЛИ

 

VT2

VT1

R1

R2

R3

Y

X2

X1

Uип

 

 

Рис.5.18. Схема электрическая логического элемента ИЛИ

 

В сериях К120ЛЛ1, К138, К155 имеются элементы, реализующие функцию ИЛИ.

3. Инвертор (элемент НЕ) – двоичный логический элемент, реализующий операцию “логическое отрицание”. Инвертор осуществляет инверсию высказывания. Логическая единица на выходе будет в том случае, если на входе будет логический нуль.

 

Логическое уравнение работы инвертора Y X

Y

X

 

Рис.5.19. Условное обозначение логического элемента НЕ

 

Таблица 5.5.

Таблица истинности инвертора

Х Y

 

R1

VT

С

Y

Rк

Uип

–Uсм

R2

X

C

 

 

Рис.5.20. Схема электрическая инвертора

 

Серийные инверторы: K155ЛH1, K131ЛН1, К136ЛН1.

Более сложными являются логические элементы, реализующие функции переключения И-НЕ, ИЛИ-НЕ.

 

X1

&

X2

И – НЕ

X1

X2

ИЛИ – НЕ

 

а) б)

X2

X1

Запрет

Y

 

 

в)

Рис.5.21. Условные обозначения логических элементов: а) – И-НЕ; б) – ИЛИ-НЕ; в) – Запрет по X₁

 

Эти элементы выпускаются в интегральном исполнении (K155ЛА3, К555ЛА3, К531ЛА1 и т.д.), фактически являясь комбинациями рассмотренных выше логических элементом И, ИЛИ, НЕ.

 

⇐ Предыдущая9101112131415161718Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: