Минимизация комбинационных логических схем на элементах высокого уровня интеграции

 

Теория конечных автоматов в настоящее время располагает методами минимизации применительно, в основном, к логическим вентильным схемам. Целью минимизации у классических методов является минимизация числа вентилей в схеме, поэтому данные методы ак­туальны лишь для схем малой степени интеграции.

Поскольку стоимость вентилей в интегральном исполнении неизмеримо мала, по сравнению с обшей стоимостью системы, для элементов высокого уровня интеграции требуются другие методы минимизации. Для системы на БИС ми­нимальная длина переключательной функции уже не гарантирует ми­нимальную сложность устройства.

Таким образом, минимизация для сложных цифровых систем бу­дет заключаться в достижении наименьшего количества схем сред­ней и большой степени интеграции для реализации конкретной фун­кции путем рационального программирования цифровых коммутаторов, оптимального совместного применения изделий цифровой электрони­ки и выбора наиболее простого схемного решения.

Рассмотрим два метода:

1. Метод построения и эквивалентных преобразований де­ревьев (для комбинационных схем).

2. Метод эквивалентных структур (для последовательностных схем).

В процессе проектирования цифровых схем всегда реализуются типовые схемные решения. Соответственно можно предложить типо­вые способы минимизации.

Этот метод эквивалентных структур состоит в том, что, один участок цепи заменяется другим, эквивалентным, выполняющим те же функции но более простым. Все такие технические решения получаются сугубо эмпирическим образом, на основе инженерного опыта. Некоторые примеры таких схемотехнических решений показаны на рисунке 6.16.

 

Рис.6.16. Примеры эквивалентных структур

 

Рассмотрим минимизацию для интегральных логических схем, реализованных в базисе MS-автоматов. Этот метод называется построение и эквивалентные преобразования деревьев МS-автоматов.

Синтезируем комбинационный MS-автомат, имеющий 5 входных переменных. Для его реализации потребуется 32-канальный MS, имеющий 5 управляющих входов. Запишем переключательную функцию такого MS в СНДФ:

 

 

(6.33)

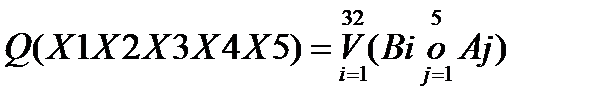
(6.34)

 

 

(6.35)

 

 

(6.36)

 

Преобразования целесообразно вести до уровня 4-х канальных МS. Такой автомат будем называть минимальным. При его реализа­ции на MS получается структура, напоминающая корни дерева. При анализе, построенного минимизированного дерева может выясниться, что отдельные корни выполняют аналогичные эквивалентные функции; либо являются логическими константами; либо реализуют элементар­ные конъюнкции или дизъюнкции; либо эти же функции с инверсией.

Признаками корней-аналогов является одинаковая коммутация всех входов этих MS из разных корней. Корни аналоги реализуют в общем случае произвольную логическую функцию. Достаточно выпол­нить такой корень один раз и подать его выходной сигнал на мес­та выходов всех выявленных корней аналогов. Остальные корни аналоги сокращаются.

Признаками корней-констант является наличие на всех инфор­мационных входах данных MS только одного настоящего логического сигнала – "0" или "1". Подставим значение константы в уравнение MS (например, "0"), то получим:

 

(6.37)

 

При любых комбинациях входных сигналов на входных aj дан­ный корень формируется на выходную MS функцию Q = 0. Такой корень можно полностью сократить, заменив его соответствующим постоян­ным логическим сигналом.

Признаками корней-вентилей является наличие на всех инфор­мационных входах таких MS только постоянных логических сигналов "О" или "1", при чем одинаковых на всех входах Bi, кроме любого одного. Например; пусть для 4-х канального MS на вход В1 по таб­лице состояний реализуемого алгоритма необходимо подать логичес­кую "1", а на вход В2,ВЗ,В4 - логический "0", тогда переключательная функция будет иметь вид:

 

. (6.38)

Полученное выражение представляет собой конъюнкцию, т.е. переключательную функцию элементарного логического вентиля "И". Он может заменить данный корень.

 

Рис.6.17. Типовые корни деревьев MS-автоматов

 

 

Алгоритм минимизации состоит в том, что:

1. корни-аналоги можно заменить на один;

2. корни-константы можно отсечь и заменить соответствующей константой;

3. корни-вентили заменяются на логические схемы элементар­ной конъюнкции (дизъюнкции).

 

Рис.6.18. Алгоритм минимизации MS-автомата

 

Еще одной возможностью минимизации является изменение пос­ледовательности подачи входных переменных на управляющие входы MS. Для разной их комбинации таблицы состояний автоматов запол­няются по разному и их коммутация информационных входов Bi всех MS, составляющих корни дерева., будет выглядеть так же по-разно­му. Таким путем можно получить несколько вариантов дерева для одного и того же алгоритма. Провести минимизацию этих автоматов и сравнением выяснить - какой из них содержит больше корней-ана­логов, корней-констант и корней-вентилей и соответственно яв­ляется более простым.

Все рассмотренные преобразова­ния относятся к одно-выходным MS-автоматам, в случае m-переменных, все операции алгоритма минимизации производят m-раз для построения m-деревьев. Во всех по­лученных деревьях выявляются корни-аналоги, корни-кон­станты и вентили, причем в этом слу­чае корни-аналоги могут объединяться и между разными де­ревьями.

 

6.1.

6.2.

6.3.

6.4.

6.5.

6.6.

6.7.

6.8.

⇐ Предыдущая12131415161718192021Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: