 |
Preprocessor > real constants > add / edit / delete > add >
|
|
|
|
Preprocessor > real constants > add / edit / delete > add >
В окне Real Constants Set Number задаем площадь поперечного сечения стержня
AREA = 0. 005.
6. 1. 5. Задаем опорные точки (рис. 5)
Путь в меню:
Preprocessor > modeling create > keypoints > in active CS >
Далее задаем координаты опорных точек (точка 1 (0; 0), точка 2 (0; -0, 2) точка 3 (0; -1)).
Рис. 5 Рис. 6
6. 1. 6. Генерируем опорные линии (рис. 6)
Путь в меню:
Preprocessor > modeling create > lines > straight line >
Соединяем опорные точки 1 и 2, являющиеся началом и концом первой линии. Аналогичным образом строим вторую линию, соединяя точки 2 и 3.
6. 1. 7. Задаем число конечных элементов на опорных линиях (рис. 7)
Путь в меню:
Preprocessor > meshing > size cntrls > picked lines >
Указываем нужную линию и вводим число конечных элементов.
6. 1. 8. Генерируем конечно-элементную модель стержня (рис. 8)
Путь в меню:
Preprocessor > meshing – mesh > lines >
Далее нажимаем pick all (генерировать элементы на всех линиях).
Рис. 7 Рис. 8
6. 2. Задаем граничные условия
6. 2. 1. Задаем условия закрепления
Путь в меню:
Preprocessor > loads > loads apply > on keypoints > displacement >
Указываем точку 1. В появившемся окне выполняем команду all dof (закрепляем все степени свободы).
6. 2. 2. Задаем условия нагружения
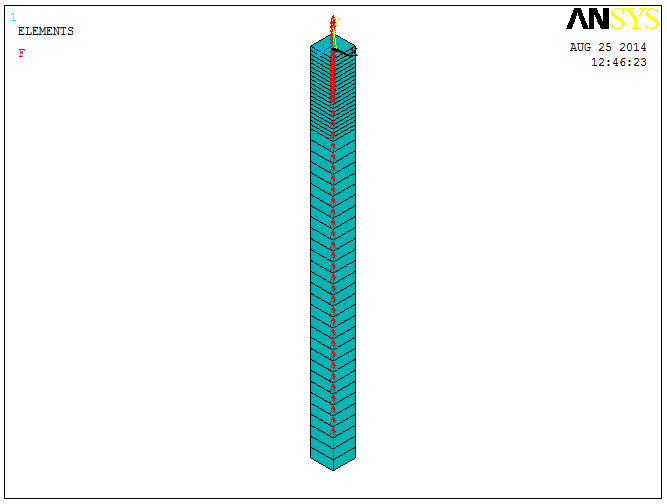
Рис. 9 Рис. 10
6. 2. 2. 1. Задаем сосредоточенные силы (рис. 9)
Путь в меню:
Preprocessor > loads > loads apply > force/moment > on keypoints
Указываем точку 2, в которой должна быть приложена сила F1.
В появившемся окне выбираем FY и задаем значение силы в соответствии с исходными данными 8000.
|
|
|
Аналогично задаем силу F2 в точке 3, равную в соответствии с исходными данными 10000.
6. 2. 2. 2. Задаем распределенную нагрузку (рис. 10):
· выбираем линию приложения распределенной нагрузки.
Путь в меню:
Utility Menu > Select > entities > lines
Указываем линию 2, на которой должна действовать распределенная нагрузка;
· выбираем узлы, принадлежащие выбранной линии.
Путь в меню:
Select > entities > nodes > attached to > lines all;
· Задаем сосредоточенные силы в узлах.
Путь в меню:
Preprocessor > loads > loads apply > force/moment > on nodes
> pick all >
В диалог-окне выбираем FY и задаем значение силы в узле;
· Выделяем все объекты.
Путь в меню:
Utility Menu > Select > everything.
6. 3. Сохраняем файл базы данных конечно-элементной модели закрепленного стержня с нагрузкой
Путь в меню:
Utility Menu > File > Save as > Save DataBase >
В появившемся окне выбираем директорию, где необходимо сохранить файл базы данных, указываем тип файла и вводим его имя.
6. 4. Запускаем программу на автоматизированный расчет
Путь в меню:
Solution > Solve current LS
6. 5. Просмотр и анализ результатов расчета
1. 6. 5. 1. Строим эпюру нормальной продольной силы Ny (рис. 11)
Вводим в командной строке: ETABLE, FYI, SMISC, 1
ETABLE, FYJ, SMISC, 1
PLLS, FYI, FYJ
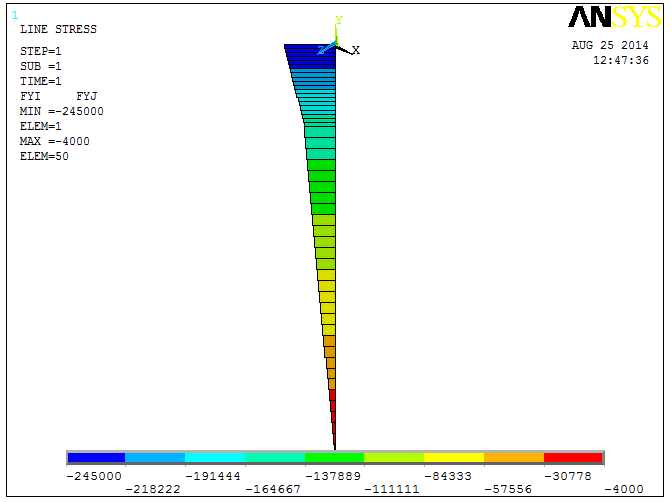
Рис. 11
6. 5. 2. Строим эпюру нормальных напряжений σ y (рис. 12)
Вводим в командной строке: ETABLE, SAXL, LS, 1
PLLS, SAXL, SAXL
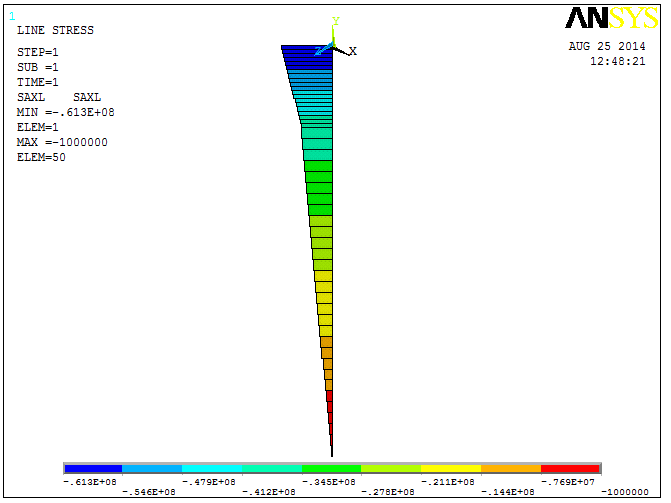
Рис. 12
6. 5. 3. Строим деформированную форму (рис. 13)
Путь в меню:
General Postproc > plot results > deformed shape
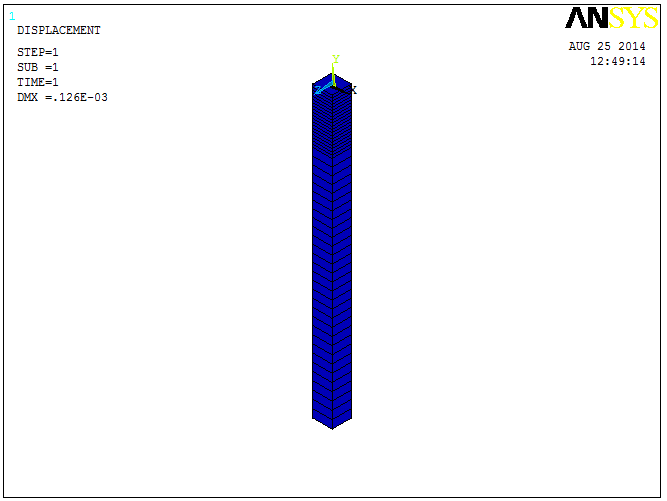
Рис. 13
6. 5. 4. Сравниваем результаты расчета в пакете ANSYS 5. 7/ED c результатами расчета методом сечений.
Максимальные нормальные напряжения возникают в поперечных сечениях стержня на первом силовом участке или линии 1. По результатам расчета методом сечений установлено, что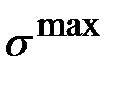 
составляет на этом участке 7 МПа. По результатам расчета в пакете ANSYS 5. 7/ED установлено, что 
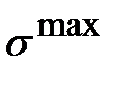составляет 7 МПа (рис. 11).
|
|
|
6. 5. 5. Проводим проверку прочности по допускаемым напряжениям
Сравним максимальные напряжения в стержне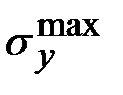 
с допускаемыми напряжениями 
:
, 
.
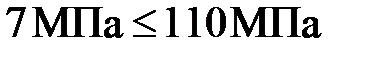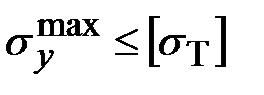Условие прочности выполняется.
6. 5. 6. Сохраняем файл базы данных модели с результатами расчета.
Путь в меню:
|
|
|
