 |
Проектирование цифрового фильтра
|
|
|
|
Проектирование цифрового фильтра
Основной недостаток аналоговых активных фильтров, подобных описанному выше, заключается в их малом порядке. Его повышение за счет применения многих звеньев низкого порядка ведет к значительному повышению габаритов фильтров и их стоимости. От этого недостатка свободны современные цифровые фильтры, число ячеек которых N даже при однокристальном исполнении может достигать десятков и сотен. Это обеспечивает повышенную частотную селекцию.
Спроектируем фильтр N+1-ro порядка класса FIR (Finite Impulse Response или с конечной импульсной характеристикой). Каждая из N ячеек временной задержки фильтра удовлетворяет следующей зависимости выходного сигнала у от входного х вида:
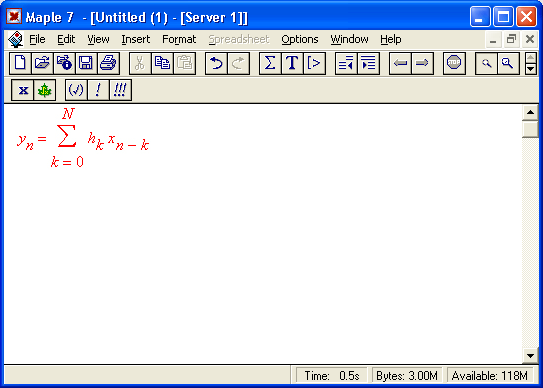
Подключим пакет расширения plots, нужный для графической визуализации проектирования:
> restart:with(p1ots):
Warning, the name changecoords has been redefined
Зададим исходные данные для проектирования полосового цифрового фильтра, выделяющего пятую гармонику из входного сигнала в виде зашумленного меандра с частотой 500 Гц:
> N:= 64: # Число секций фильтра (на 1 меньше порядка фильтра)
> fs:= 10000: # Частота квантования
> fl = 2300: # Нижняя граничная частота
> fh = 2700: # Верхняя граничная частота
> m:= 10: # 2^m > N - число точек для анализа
Вычислим:
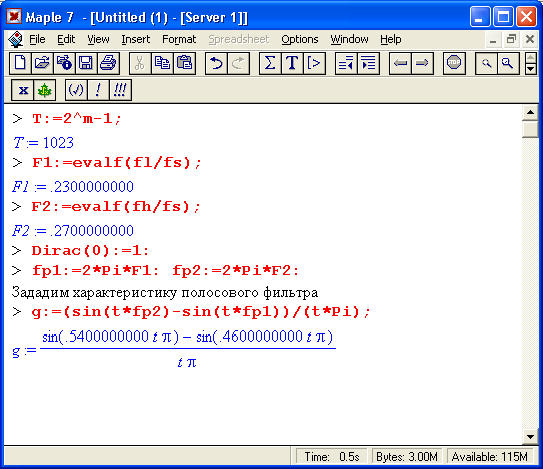
Вычислим FIR-коэффициенты для прямоугольного окна фильтра:
> С:-=(n) -> limit(g,t=n):h:= aray(0..N): N2:=N/2:
> for n from 0 to N2 do h[N2-n]:= evalf(C(n)); h[N2+n]:= h[N2-n]; od:
Определим массивы входного x(n) и выходного у(n) сигналов:
> х:= array(-N..T): y:= аггау(0..Т):
Установим значение х(n) равным 0 для времени меньше 0 и 1 для времени >=0:
> for n from -N to -1 do x[n]:= 0; od:
> for n from 0 to Т do x[n]:= Dirac(n); od:
Вычислим временную зависимость для выходного сигнала:
> for n from 0 to Т do y[n]:= sum(h[k]*x[n-k],k=0..N): od:
|
|
|
Построим график импульсной характеристики фильтра, отражающей его реакцию на сигнал единичной площади с бесконечно малым временем действия:
> р:= [seq([j/fs,y[j]],j=0..T)3:
> plot(p, time=0..3*N/fs, labels=[time,output], axes=boxed, xtickmarks=4, title-'Иипульсная характеристика фильтра',color=black);
Он показан на рис. 17.19. Нетрудно заметить, что эта характеристика свидетельствует об узкополосности фильтра, поскольку его частоты fl и fh различаются несильно. В этом случае полосовой фильтр по своим свойствам приближается к резонансному, хотя само по себе явление резонанса не используется.
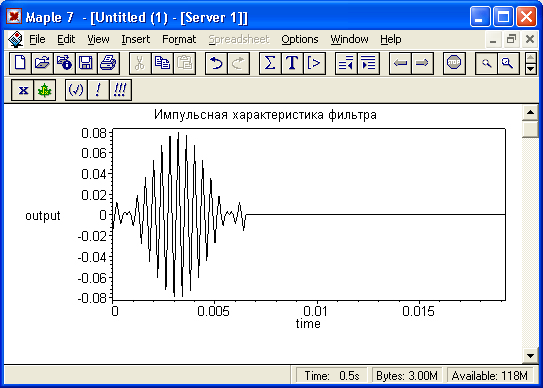
Рис. 17.19. Импульсная характеристика цифрового фильтра
Вычислим АЧХ фильтра, используя прямое преобразование Фурье. Оно после подготовки обрабатываемых массивов реализуется функцией FFT:
> rо:= array (1..T+1): io:= arrayd..T+l):
> for n from 0 to Т do ro[n+l]:- y[n]; io[n+l]:= 0; od:
> FFT(m,ro,io):
Построим график АЧХ фильтра:
> р:=[seq([j*fs/(T+l),abs(ro[j+l]+io[j+l]*I)3,j=O..T/2)]:
> plot(p, frequency=0..fs/2, tabels=[frequency,gain], tit1e='AЧX фильтра',со1ог=black);
Он представлен на рис. 17.20. Нетрудно заметить, что и впрямь АЧХ фильтра напоминает АЧХ резонансной цепи — она имеет вид узкого пика. Вы можете легко проверить, что раздвижением частот fl и fh можно получить АЧХ с довольно плоской вершиной и резкими спадами (говорят, что такая характеристика приближается к прямоугольной).
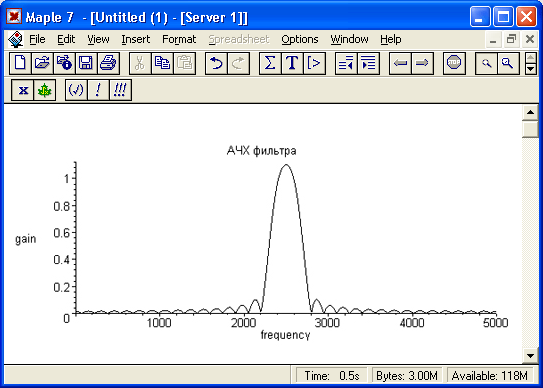
Рис. 17.20. АЧХ цифрового полосового фильтра
Теперь приступим к тестированию фильтра. Зададим входной сигнал в виде зашумленного меандра с частотой 500 Гц и размахом напряжения 2 В:
> 1:=round(fs/2/500):
> for n from 0 by 2*1 to Т do
> for n2 from 0 to 1-1 do
> if n+n2 <= Т then
> x[n+n2]:= evalf(-l+rand()/10^12-0.5);
> fi:
> if n+n2+1 <= Т then
> x[n+n2-H]:-=eva1f(l+ranoX)/10^12-0.5);
> fi;
> od:
> od:
Временная зависимость синтезированного входного сигнала представлена на рис. 17.21.
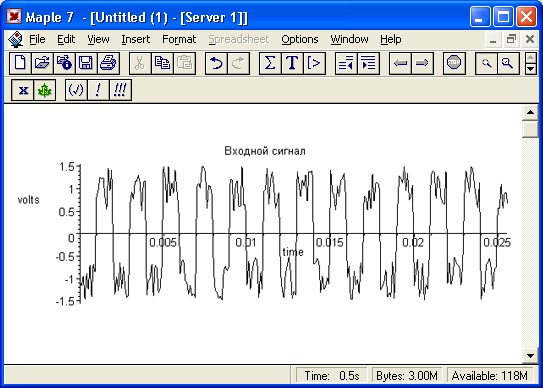
Рис. 17.21. Синтезированный входной сигнал
Вычислим реакцию фильтра на входной сигнал:
> for n from 0 to T do
> y[n]:= sum(h[k]*x[n-k],k=0..N);
> od:
Построим график выходного сигнала:
|
|
|
> р:= [seq([j/fs, x[j]], j=0..T)]:q:= [seq([j/fs, y[j]], j =0..Т)]:
> plot(p,time=0..T/fs/4,1abels=[time,volts],title='Входной сигнал\сolor=black);
> plot(q,tine=0..T/fs/4,1abels=[tirae,volts], titlе='Выходной сигнал",color=black);
Временная зависимость выходного сигнала показана на рис. 17.22. Нетрудно заметить, что в конце концов выходной сигнал вырождается в пятую гармонику входного сигнала, но этому предшествует довольно заметный переходной процесс. Он связан с узкополосностью данного фильтра.
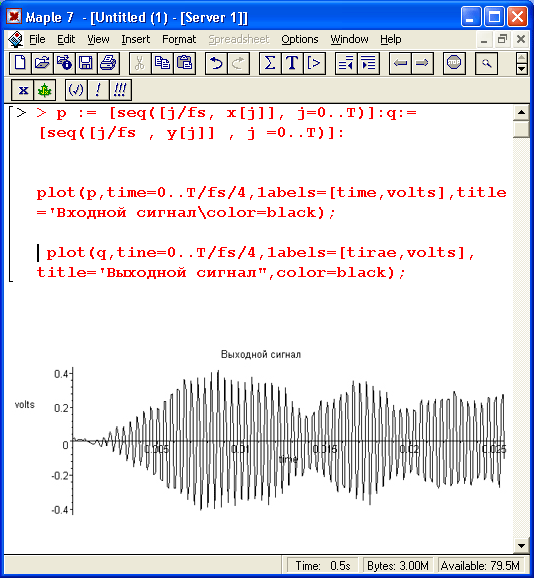
Рис. 17.22. Временная зависимость выходного сигнала цифрового фильтра
Вычислим спектры входного и выходного сигналов, подготовив массивы выборок сигналов и применив прямое преобразование Фурье с помощью функции FFT:
> Н:= array(l..T+l):1i:=array(1..Т+1):
> for n from 0 to T do,
> ri[n+l]:= x[n]*2/T: ii[rn-l]:= 0;
> ro[n+l]:= y[n]*2/T; Io[rrfl]:= 0;
> od:
> FFT(m.ri,ii):rTT(m,ro,io):
Построим график спектра входного сигнала, ограничив масштаб по амплитуде значением 0,5 В:
> р:= [seq([j*fs/(T+l),abs(n[j+l]+ii[j-H]*I)],j=0..T/2)]:
> q:= [seq([j*fs/(T-H),abs(ro[j-H]+To[j+l]*I)],j=0..T/2)]:
> plot(p, frequency=0..fs/2,y0..0.5,labe1s=[Частотa.V],title='Частотный спектр входного сигнала',color=black);
Этот график представлен на рис. 17.23. Из него хорошо видно, что спектральный состав входного сигнала представлен только нечетными гармониками, амплитуда которых убывает по мере роста номера гармоники. Пятая гармоника на частоте 2500 Гц находится посередине полосы пропускания фильтра, ограниченной граничными частотами фильтра 2300 и 2700 Гц. Заметны также беспорядочные спектральные линии шума сигнала в пределах полосы прозрачности фильтра.
Теперь построим график спектра выходного сигнала:
> p1ot(q, frequency=0..fs/2,y=0..0.5,labe1s=[Частотa,V], title='Частотный спектр выходного сигнала'бcolor=black);
Он представлен на рис.17.24. Хорошо видно эффективное выделение пятой гармоники сигнала и прилегающей к ней узкой полосы шумового спектра.
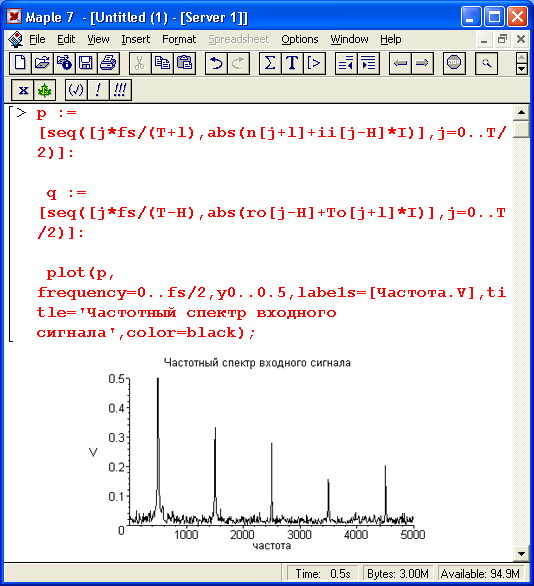
Рис. 17.23. Спектрограмма входного сигнала
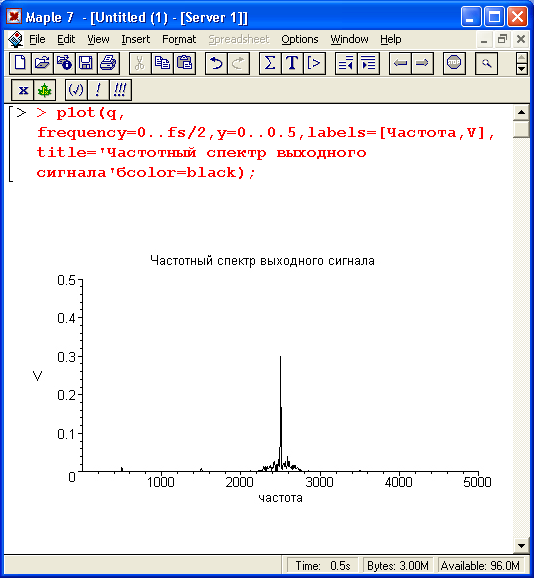
Рис. 17.24. Спектрограмма выходного сигнала цифрового фильтра
Приведенные данные свидетельствуют, что спроектированный фильтр полностью отвечает заданным требованиям и обеспечивает уверенное выделение пятой гармоники зашумленного меандра. По образу и подобию данного документа можно выполнить проектирование и других видов цифровых фильтров.
Gif

Gif

Gif

Gif

Gif

Gif
|
|
|

Gif

Gif

|
|
|


