 |
Интерполяция и аппроксимация функциональных зависимостей
|
|
|
|
Интерполяция, экстраполяция и аппроксимация
Вычисление многих функций, особенно специальных, требует больших затрат времени. Поэтому до сих пор широко применяются таблицы таких функций. Достаточно отметить знаменитые на весь мир таблицы в книге «Справочник по специальным функциям с формулами, графиками и таблицами» под редакцией М. Абрамовица и И. Стиган [59].
Если некоторая зависимость у(х) представлена рядом табличных отсчетов y(x), то интерполяцией принято называть вычисление значений у(х) при заданном х, расположенном в интервале между отсчетами. За пределами общего интервала определения функции [а,b], то есть при х < а и х > b, вычисление у(х) называют экстраполяцией (или иногда предсказанием значений функции). В данном случае речь идет об одномерной интерполяции, но возможны двумерная интерполяция функций двух переменных z(x, у) и даже многомерная интерполяция для функций многих переменных.
Интерполяция и экстраполяция часто выполняются по некоторой скрытой, но подразумеваемой зависимости. Например, если узловые точки функции соединить отрезками прямых, то будем иметь многоинтервальную линейную интерполяцию данных. Если использовать отрезки параболы, то интерполяция будет параболической. Особое значение имеет многоинтервальная сплайн-интерполяция, области применения которой уже сейчас весьма обширны и непрерывно расширяются. Интерполяция рядом Фурье (набором синусоидальных функций) также достаточно хорошо известна; она эффективна при интерполяции периодических функций.
Аппроксимацией в системах компьютерной математики обычно называют получение приближенных значений какого-либо выражения. Однако под аппроксимацией функций подразумевается получение некоторой конкретной функции, вычисленные значения которой с некоторой точностью аналогичны аппроксимируемой зависимости. Обычно предпочитают найти одну зависимость, приближающую заданный ряд узловых точек. Часто для этого используют степенные многочлены — полиномы.
|
|
|
Здесь мы будем рассматривать такие виды аппроксимации, которые дают точные значения функции у(х) в узловых точках в пределах погрешности вычислений по умолчанию. Если аппроксимирующая зависимость выбирается из условия наименьшей среднеквадратической погрешности в узловых точках (метод наименьших квадратов), то мы имеем регрессию или приближение функций по методу наименьших квадратов.
Аппроксимация аналитически заданных функций
Аппроксимация аналитически заданных функций
Если функция задана аналитически, то наиболее простым способом нахождения ее аппроксимирующей зависимости является применение функции convert. Это поясняют следующие примеры:

На рис. 9.4 представлен пример полиномиальной аппроксимации хорошо известной статистической функции erfc(x). Для полинома задана максимальная степень 12, но ввиду отсутствия в разложении четных степеней максимальная степень результата оказывается равна 11.
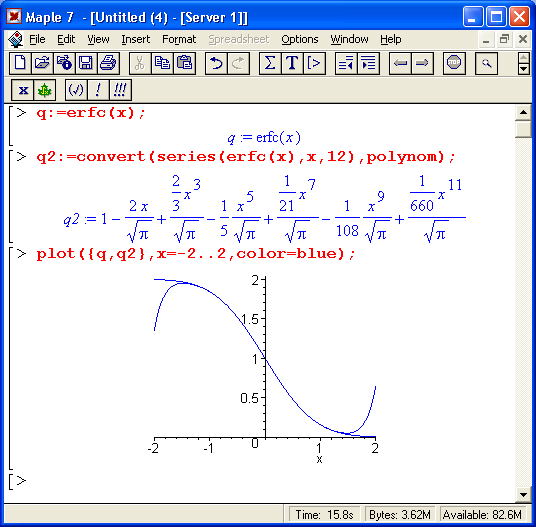
Рис. 9.4. Пример полиномиальной аппроксимации функции erfc(x)
Как видно из приведенного рисунка, в интервале изменениях от -1,5 до 1,5 аппроксимирующее выражение почти повторяет исходную зависимость. Однако затем график аппроксимирующей функции быстро отходит от графика исходной зависимости. При этом он ведет себя иначе даже качественно, никоим образом не показывая асимптотическое поведение, характерное для исходной зависимости.
Gif

Gif

Полиномиальная интерполяция табличных данных
|
|
|


