Краткие теоретические сведения

Основные формулы и уравнения

Истечение газов и паров

При решении задач, связанных с истечением газа через сопла (насадки) (рисунок 15), чаще всего приходится определять скорость истечения и расход, т. е. количество газа, вытекающего в единицу времени. В этих случаях необходимо прежде всего найти отношение p₂/p₁,

где р₂ — давление среды на выходе изсопла;

P₁ — давление среды на входе в сопло.

Полученное числовое зна­чение p₂/p₁ сравнивают с так называемым критическим отношением давлений для данного газа, определяемым иωз равенства

 

)кр. = ( (109)

 

Рисунок 15 – Газ, проходящий через сопло

и равным:

для одноатомных газов при k = 1,67

(p₂/p₁)_KP = 0,487;

для двухатомных газов при k = 1,4

(p₂/p₁)_KP = 0,528;

для трех- и многоатомных газов при k = 1,29

(p₂/p₁)_KP = 0.546.

Если адиабатное истечение газа происходит при (p₂/p₁) > (p₂/p₁)_KP то теоретическая скорость газа у устья суживающегося сопла определяется по формуле

w = .. (110)

где k — показатель адиабаты;

V₁ — удельный объем газа на входе в сопло. Заменяя для идеального газа в формуле (110) Р₁V₁ на RT, получаем

w = .. (111)

В формулах (110) и (111) значения р, v и R даны соот­ветственно в следующих единицах: Па, кг/м³ и Дж/(кг*К).

Теоретическая скорость газа может быть также най­дена по формуле:

w = .. (112)

где i₁ и i₂.—соответственно энтальпии газа в начальном и конечном состояниях в Дж/кг.

Если значения i выражены в кДж/кг, то формула (112) принимает вид

w = = 44,76

Во всех приведенных случаях скорость w получается в м/с.

Расход газа определяется по формуле

M = .. (113)

где f—выходное сечение сопла в м²

Если же адиабатное истечение газа происходит при (p₂/p₁)£ (p₂/p₁))_кр,то теоретическая скорость газа в устье суживающегося сопла будет равна критической скорости и определится по уравнению

w = 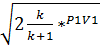. (114)

Критическая скорость по формуле (114) зависит только от начального состояния газа и показателя адиабаты k. Поэтому, подставляя значение к для различных рабочих тел, получим более удобные формулы для определения критической скорости. В частности, для двухатомных газов

w_кр= 1,08 .. (115)

или

wк_р = 1,08 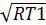.. (116)

Критическая скорость может быть также определена по одной из следующих формул:

w_кр = ..

w_кр = 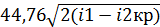.. (117)

 

i - энтальпия газа при критическом давлении р_кр.

В первой формуле энтальпия выражена в Дж/кг, во второй — в кДж/кг. Расход газа в этом случае будет максимальным и быть вычислен по уравнению

M = .. (118)

Подставляя в эту формулу значение k, получаем: для двухатомных газов

М_mах = 0,686f .. (119)

для трехатомных газов

М_mах = 0,686f .. (120)

Во всех перечисленных формулах следует брать р в Па, v — в м³/кг. Расход газа получается в кг/с.

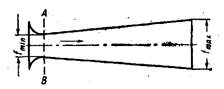
Рисунок 16 - Сопло Лаваля

 

Для получения скоростей истечения выше критических (сверхзвуковые скорости) применяется расширяющееся сопло, или сопло Лаваля (рисунок 16) В минимальном сечении сопла Лаваля скорость движения газа равна критической скорости или скорости звука, определяемой пара­метрами р_кр и v_кр.

Площадь минимального сечения сопла определяется по формуле причем для двухатомных газов она может быть определена также по формуле

f_min = M_maxV_кр/w_кр (121)

причем для двухатомных газов она может быть определена также по формуле

f_min = ....(122)

а для трехатомных газов

f_min = .. (123)

Площадь выходного сечения сопла

f₂ = f _min 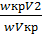… (124)

где v₂ = v₁ удельный объем газа при давле­нии среды р₂.

Длину расширяющейся части сопла находят по урав­нению

l = .. (125)

где d и d_mln - соответственно диаметры выходного и ми­нимального сечений;

<— угол конусности расширяющейся части сопла.

При истечении водяного пара все общие законы, уста­новленные для истечения газов, остаются в силе. Однако формулы истечения для газов, в которые входит вели­чина k, для водяного пара будут приближенными, так как значение k для пара в процессе изменения его состоя­ния непостоянно.

В связи с этим при истечении водяного пара для точ­ных расчетов следует применять следующие формулы:

,

для определения скорости – формулу (112), а для определения расхода пара — формулу

M= .. (126)

При 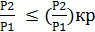для определения критической скорости следует применять формулы (117), а для определения расхода – любую из следующих формул:

М_max = или

М_max = . (127)

В первой формуле i_t и i_KP выражены в Дж/кг, во второй — в кДж/кг.

Площади поперечных сечений сопла определяют по формулам:

f_min = M_maxV_кр/w_кр или

f = 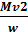.. (128)

Длину расширяющейся части сопла находят по формуле (125).

Истечение с учетом сопротивлений

Действительная скорость истечения всегда меньше теоретической, так как процесс истечения связан с наличием трения. Если обозначить действительную скорость течения через w_д, то потеря кинетической энергии струи

Откуда (129)

w_д = w

Обозначая = φ,

Получаем

w_д = w′ = φ w (130)

Коэффициент φ называют скоростным коэффициентом сопла, а коэффициент

ξ = 1 – φ^2.. (131)

коэффициентом потери энергии в сопле.

Часть кинетической энергии в результате трения пре­вращается в теплоту, которая при отсутствии теплообмена повышает энтальпию и энтропию рабочего тела, вытекаю­щего из сопла. Поэтому состоя­ние газа или пара в конце дейст­вительного, процесса истечения в диаграмме is изображается точкой, всегда расположенной правее точки, характеризующей конечное состояние рабочею тела в идеальном процессе исте­чения.

Рисунок 17 – Диаграмма действительного истечения газа через сопло

Пользуясь диаграммой is, можно определить. параметры в конце процесса расширения. Если дана начальная точка А (рисунок 17) и коэффициент ξ (или φ), то, проводя адиа­бату АВ, откладывают от точки В вверх отрезок ВС = i₂ – i₂д и — «ад» и, проведя через точку С горизонталь до пересечения с конечной изобарой р₂, получают точку D, характеризующую состояние рабочего тела в конце дей­ствительного процесса истечения. По ней можно найти необходимые параметры пара: удельный объем, степень сухости и т.д.

Если же даны начальное и конечное состояние, т. е. точки А и D, то очень легко изобразить потери работы в виде отрезков, проведя через точку D горизонталь до пе­ресечения ее с адиабатой. Отношение отрезков СВ/А В даст значение, коэффициента потери энергии, а следова­тельно, и скоростного коэффициента.

Дросселирование (мятие) газов и паров

При прохождении газа или пара через суженное сечение происходит снижение его давления. Этот процесс называют дросселированием, или мятием.

В процессе дросселирования газа или пара наряду со снижением давления всегда возрастает удельный объем. Температура идеальных газов при дросселировании остается неизменной, температура же реальных газов остается постоянной лишь при одной, определенной начальной температуре газа, называемой температурой инверсии; приближенное значение этой температуры определяется из выражения

Т_инв = 6,75Ткр (132)

Ткр — критическая температура газа или пара в К.

Если же температура подвергающегося дросселированию газа отлична от температуры инверсии, то его температура изменяется; уменьшается, если температура газа меньше температуры инверсии и увеличивается, если температура его больше температуры инверсии.

С достаточной точностью можно принять, что при дросселировании энтальпия газа или пара в начальном и конечном состояниях одинакова, т. е.

i₁ = i₂

Дросселирование — процесс необратимый, поэтому он не может быть изображен в термодинамической диаграмме им-либо графиком.

Задачи, связанные с дросселированием пара, обычно сводятся к определению параметров состояния пара после дросселирования. Проще всего они решаются при помощи диаграммы is.

Рисунок 18 – Диаграмма дросселирования пара

 

Так как в начальном и конечном состояниях энтальпия пара одинакова, то конечное состояние пара определяется пересечением горизонтали, проходящей через начальную точку 1(рисунок 18), с изобарой конечного давления Р₂.Точка 2 определяет все параметры после дросселирования.

Примеры решения задач

1 Воздух из резервуара с постоянным давлением Р₁=10МПа и температурой t₁ = 15° С вытекает, в атмосферу через трубку с внутренним диаметром 10 мм.

Найти скорость истечения воздуха и его секундный расход. Наружное давление принять равным 0,1 МПа. Процесс расширения воздуха считать адиабатным.

 

Решение:

Определяем отношение р₂/р₁. Оно равно 1/100 и, сле­довательно, меньше критического отношения давлений для воздуха, составляющего 0,528. Поэтому скорость истечения будет равна критической и определится по формуле (116):

w_кр =1,08 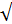RT_t = 1,08 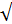287* 288 = 310 м/с.

Секундный расход находим по формуле (119):

М_mах = 0,686 f ,

f = = = 0,0000785 м²

V₁ = = = 0,00827 м³/кг

следовательно,

М_mах = 0,686*0,0000785 = 1,87 кг/с.

Ответ: М_mах = 1,87 кг/с

2. В резервуаре, заполненном кислородом, поддер­живают давление р₁ = 5 МПа. Газ вытекает через су­живающее сопло в среду с давлением 4 МПа. Начальная температура кислорода 100° С.

Определить теоретическую скорость истечения и рас­ход, если площадь выходного сечения сопла f = 20 мм². Найти также теоретическую скорость истечения кислорода и его расход, если истечение будет происходить в атмосферу. В обоих случаях считать истечение адиабат­ным. Барометрическое давление принять равным 0,1 МПа.

Решение:

Отношение давлений составляет

Р₂/Р₁ = 40/50 = 0,8 ˃ (Р2/Р1)кр = 0,528;

следовательно, скорость истечения меньше критической и определяется по формуле (110):

w =

Из характеристического уравнения

V₁ = RT₁/P₁ = 259,8 * 373/5*10⁶ = 0,01194 м³/кг

Все остальные величины, входящие в формулу (110),

известны.

Подставляя их значения, получаем

w = ] = 205 м/с

Секундный расход найдем по формуле (113):

M = ]

 

M = 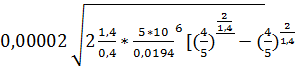] = 0,175 кг/с

При истечении в атмосферу отношение давлений

Р₂/Р₁ = 1/50 < (Р₂/Р₁)кр. = 0,528;

следовательно, скорость истечения в этом случае будет равна критической, а расход— максимальным. По формуле (116)

w_кр = 1,08 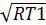= 1,08 wк_р = 1,08 = 336 м/с

Максимальный расход определится по формуле. (120):

М_mах = 0,686f

М_шах = 0,686.0,00002 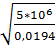= 0,22 кг/с.

 

Ответ: М_шах =0,22 кг/с; w_кр =336 м/с; M = 0,175 кг/с; w = 205 м/с

 

⇐ Предыдущая6789101112131415Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: