Краткие теоретические сведения

Основные формулы и уравнения

Круговые процессы

Круговым процессом, или циклом, называют совокуп­ность термодинамических процессов, в результате осу­ществления которых рабочее тело возвращается в исход­ное состояние.

Рисунок 19 – Работа кругового цикла на диаграмме РV

 

Рисунок 20 – Работа кругового цикла на диаграмме TS

Работа кругового процесса: (l₀) изображается в диа­грамме pv (рисунок 19) площадью, заключённой внутри зам­кнутого контура цикла, причем работа положительна, если цикл совершается по часовой стрелке (прямой цикл), и отрицательна, если он совершается против часовой стрелки (обратный цикл).

Прямой цикл (l₀ > 0) характерен для тепловых двигателей, обратный цикл l₀ < 0) — для холодильных машин.

Если обозначитьчерез:

ｑ₁ - количество теплоты, заимствованной 1 кг рабочего тела от внешнего (или верхнего), источника теплоты;

ｑ₂ - количество теплоты, отданной 1 кг рабочего тела внешнему охладителю (или нижнему источнику), то полезно использованная в цикле теплота

l_o =ｑ₁ -ｑ₂ (133)

Это количество теплоты в диаграмме Ts изображается площадью, заключенной внутри замкнутого контура цикла (рисунок 20). Очевидно, эта площадь представляет также величину работы за один цикл, причем, как и в диаграм­ме PV,работа положительна, если цикл совершается по часовой стрелке, и отрицательна, если он совершается против часовой стрелки.

Степень совершенства процесса превращения теплоты в работу в круговых процессах характеризуется термиче­ским кпд

η_t =ｑ₁ -ｑ₂/ｑ₁ = l_o/ｑ₁ (134)

Пользуясь диаграммой TS(pисунок 20), можно определить термический кпд цикла графическим путем:

η_t = пл. ABCD/ пл. АВСС'А'

Цикл Карно

Цикл Карно состоит из двух адиабат и двух изотерм (рисунок 21 и 22). Количество подведенной теплоты

ｑ₁ = RT₁lnV₂/V₁ (135)

 

Рисунок 21-. Цикл Карно в осях PV

Рисунок 22 - Цикл Карно в осях TS

Количество отведенной теплоты (абсолютное значение)

ｑ₂ = RT₂lnV₃/V₄ (136)

Работа цикла Карно по уравнению (133)

l_o =ｑ₁ -ｑ₂

Термический кпд цикла

η_t = T₁-T₂/T₁ = 1 – T₂/T₁ (137)

где Т₁ и Т₂— соответственно температуры верхнего и нижнего источника теплоты в К.

Теоретические циклы поршневых двигателей внутреннего сгорания

Цикл с подводом теплоты при постоянном объеме состоит из двух адиабат и двух изохор (рисунок 23 и 24). Характеристиками цикла являются:

ε = V₁/V₂ — степень сжатия;

λ = р₃/р₂ — степень повышения давления.

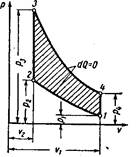
Рисунок 23 – Цикл с подводом теплоты при постоянном объеме в осях PV

Рисунок 24 – Цикл с подводом теплоты при постоянном объеме в осях TS

 

Количество подведенной теплоты

ｑ₁ = с_v (T₃ – T₂)

Количество отведенной теплоты (абсолютное значение)

ｑ₂ = с_v (T₄ – T₁)

Работа цикла

l_o =ｑ₁ -ｑ₂

Термический кпд цикла

η_t = 1 - 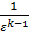.. (138)

Цикл с подводом теплоты при постоянном давлении состоит из двух адиабат, одной изобары и одной изохоры (рисунок 25 и 26).

Рисунок 25 - Цикл с подводом теплоты при постоянном давлении в осях PV

 

Рисунок 26 - Цикл с подводом теплоты при постоянном давлении в осях TS

 

Характеристиками цикла являются:

ε = V₁/V₂ — степень сжатия;

ρ = V₃/V₂ -—степень предварительного расширения.

Количество подведенной теплоты

ｑ₁ = с_p (T₃ – T₂)

 

Количество отведенной теплоты (абсолютное значение)

ｑ₂ = с_p (T₄ – T₁)

 

Работа цикла

l_o =ｑ₁ -ｑ₂

Термический кпд цикла

η_t = 1 - 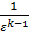….. (139)

Цикл с комбинированным подводом теплоты состоит из двух адиабат, двух изохор и одной изобары (рисунок 27 и 28).

Характеристиками цикла являются:

ε= V₁/V₂; λ = Р₃/Р₂; ρ = V₄/V₃.

Рисунок 27 – Цикл с комбинированным подводом теплоты в осях PV

 

Рисунок 27 – Цикл с комбинированным подводом теплоты в осях TS

 

Количество подведенной теплоты

ｑ₁ = с_v (T₃ – T₂) + с_p (T₄ – T₃)

Количество отведенной теплоты (абсолютное значение)

ｑ₂ = с_v (T₅ – T₁)

Термический кпд цикла

η_t = 1 - 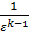….. (140)

Во всех приведенных выше теоретических циклах поршневых двигателей внутреннего сгорания уравнения для определения количества подведенной и отведенной теплоты, а также для термического кпд даны для случая с = const.

Циклы газотурбинных установок

На рисунке 28 представлена схема наиболее распространенного типа газотурбинной установки со сгоранием топ­лива при постоянном давлении.

Компрессор К, расположенный на одном валу с газо­вой турбиной Т, всасывает воздух из атмосферы и сжимает его до заданного давления.

Рисунок 28 – Схема газотурбинной установки со сгоранием топлива при постоянном давлении

Сжатый в компрессоре воздух поступает в камеру сгорания КС; туда же топливным насосом ТЕ подается жидкое горючее. Сгорание происхо­дит при постоянном давлении. Из камеры сгорания газы поступают в сопла С, из которых они с большой скоростью поступают на рабочие лопатки Л турбины и приводят во вращение ее ротор. Отработавшие газы через выпускной патрубок П выпускаются в атмосферу.

На рисунке 29 дан теоретический цикл газовой турбины с подводом теплоты при постоянном давлении. Как видно из этого рисунка, цикл.состоит из двух адиабат и двух изобар. Линия 1—2 изображает процесс адиабатного сжа­тия в компрессоре, 2—3 — изобарный подвод теплоты (сгорание топлива), 3—4— адиабатное расширение в га­зовой турбине, 4—1 — условный изобарный процесс, за­мыкающий цикл.

Термический кпд цикла

η_t = 1 - 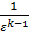.. (141)

или

η_t = 1 - .. (142)

где ε= V₁/V₂ — степень сжатия, а λ = Р₂/Р₁ — степень повышения давления.

 

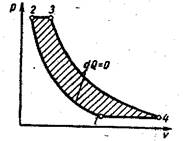
Рисунок 29 - Цикл газовой турбины с подводом теплоты при постоянном давлении.

Рисунок 30 - Цикл газотурбинной установки с подводом теплоты при постоянном объеме

Цикл газотурбинной установки с подводом теплоты при постоянном объеме представлен на рисунке 30, а схема установки дана на рисунке 31. В компрессоре К происходит адиабатное сжатие воздуха (линия 1—2, рисунок 30). Сжатый воздух постyпает в камеру сгорания КС, куда одновре­менно топливным насосом ТН подается жидкое топливо. Сгорание происходит при постоянном объеме (при закрытых клапанах). Воспламенение горючей смеси обычно производится от электрической свечи ЭС. Продукты сгорания проходят через выпускной клапан камеры, поступают в сопла С, где адиабатно расширяются (линия 3—4, рисунок 30).

Рисунок 31 - Схема газотурбинной установки

 

Далее газы с большой скоростью поступают на рабочие лопатки Л турбины и приводят во вращение ее ротор. Отработавшие газы через выпускной патрубок П выпускаются в атмосферу. Цикл замыкается условным изобарным процессом (линия 4—1, рисунок 30). Термический кпд цикла

η_t = 1 - 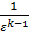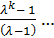. (143)

где

λ = Р₃/Р₂

Так как уходящие из газовой турбины продукты сгорания имеют достаточно высокую температуру, то для повышения экономичности газотурбинного агрегата вво­дят так называемую регенерацию, т. е. предварительный подогрев сжатого в компрессоре воздуха за счет теплоты уходящих газов. Термический кпд цикла газовой тур­бины при наличии регенерации больше, чем термический кпд турбины без регенерации.

 

Рисунок 32 - Цикл газовой турбины с подводом теплоты при р = const и регенерацией

Рисунок 33 - Цикл газовой турбины при V = const и регенерацией

 

Если всю располагаемую теплоту отработавших газов использовать для подогрева воздуха, то такой цикл газо­вой турбины носит название цикла с предельной регенера­цией.

Цикл газовой турбины с подводом теплоты при р = const и регенерацией изображен на рисунке 32, а цикл турбины при V = const и регенерацией — на рисунке 33. В обоих циклах линии 2—3 изображают изобарный подогрев сжатого воздуха в регенераторе, а линии 5—6 — изобарное охлаждение продуктов сгорания в регенераторе.

Термический кпд цикла турбины с подводом теп­лоты при р = const с предельной полной регенерацией и адиабатным сжатием.

η_{t рег} = 1 – Т₁/Т₅

Термический кпд цикла турбины с подводом теп­лоты при v = const с предельной регенерацией и адиабатным сжатием

η_{t рег} = 1 –

Поршневые компрессоры

На рисунке 34 в диаграмме pv изображены процессы, про­текающие в идеальном компрессоре. Линия 4—1 изображает процесс всасывания газа, кривая 1—2— процесс сжатия и линия 2 — 3 — процесс нагнетания.

Диаграмму 1—2 — 3 — 4 называют теоретической индикаторной диаграммой.

 

Рисунок 34 - Процессы, протекающие в идеальном компрессоре в осях PV

Рисунок 35 - Работа компрессора l₀ определяется площадью индикаторной диаграммы и зависит от процесса сжатия

 

Теоретическая работа компрессора l₀ определяется площадью индикаторной диаграммы и зависит от процесса сжатия (рисунок 35). Кривая 1— 2 изображает процесс изо­термического сжатия, кривая 1—2" — адиабатного сжа­тия и кривая 1—2' — политропного сжатия.

При изотермическом сжатии теоретическая работа компрессора равна работе изотермического сжатия:

l₀ = P₁V₁lnP₂/P₁ = RT lnP₂/P₁ (144)

Если масса всасываемого воздуха М кг, а объем его V₁ м³, то

l₀ = P₁ ln P₂/P₁ (145)

Работа, отнесенная к 1 м³ всасываемого воздуха,

l´₀ = P₁lnP₂/P₁ (146)

Работа для получения 1 м³ сжатого воздуха

l´´₀ = P₂ ln P₂/P₁

Количество теплоты, которое должно быть отведено при изотермическом сжатии,

q = l₀ или Q = L

При адиабатном сжатии теоретическая работа компрессора в k раз больше работы адиабатного сжатия:

l₀= .. (147)

Если масса всасываемого воздуха М кг, а объем его V₁ м³, то

L₀= .. (148)

Работа, отнесенная к 1 м³ всасываемого воздуха,

l´₀= .. (149)

Работа для получения 1 м³ сжатого воздуха

l´´₀= .. (150)

Температуру газа в конце сжатия можно определять из соотношения параметров адиабатного процесса.

Работа компрессора при адиабатном сжатии может быть также найдена по формуле

l₀ = i₂ – i₁ (151)

где i₁ и i₂ - соответственно начальное и конечное зна­чения энтальпии воздуха.

Эта формула весьма удобна для подсчета работы идеаль­ного компрессора при адиабатном сжатии с помощью диаграммы is.

В этом случае из точки 1(рисунок 36), характеризующей начальное состояние, проводят вертикальную линию до пе­ресечения ее в точке 2 с изобарой р₂. Ординаты точек 1 и 2 дают значения энтальпии i₁ и i₂, а отрезок 1—2—их разность.

Рисунок 36 – Диаграмма работы идеального компрессора в осях is при

адиабатном сжатии

При политропном сжатии теоретическая работа компрессора в т раз больше работы политропного сжатия:

l₀= 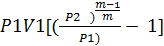.. (152)

Если масса всасываемого воздуха М кг, а объем его V₁ м³, то

L₀= 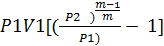.. (153)

Работа, затрачиваемая на сжатие 1м³ всасываемого воздуха,

l ₀= 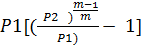.. (154)

Работа для получения 1 м³ сжатого воздуха

l ₀= .. (155)

Количество теплоты, которое должно быть отведено при политропном сжатии, находят по формуле

ϥ = с(t₂ – t₁) = c_v (t₂ – t₁) (156)

Все приведенные выше формулы для определения ра­боты компрессора дают абсолютную величину работы.

Теоретическая мощность двигателя для привода ком­прессора

N = .. (157)

 

N = .. (158)

 

N = .. (159)

В формулах (144)—(159) значения р, v, l_Q, L₀, l´_o, l´´₀ даны соответственно в следующих единицах;

р₁ и р₂ — в Па;

v (объем всасываемого или сжатого воздуха) — в м³/ч;

l₀ — в Дж/ч;

l´_о и l´´_о — в Дж/м³;

N — в кВт.

Действительная индикаторная диаграмма значительно отличается от теоретической главным образом вследствие наличия в действительном компрессоре вредного простран­ства, потерь давления во впускном и нагнетательном кла­панах и теплообмена между газом и стенками цилиндра.

При наличии вредного пространства (рисунок 37) в инди­каторную диаграмму вводится добавочный процесс (ли­ния 3—4) — процесс расширения сжатого газа, оставше­гося к концу нагнетания во вредном пространстве ци­линдра.

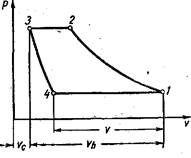
Рисунок 37 – Действительная индикаторная диаграмма

 

Отношение объема вредного пространства к объему, описываемому поршнем, т. е. величину а = Vс/V_h, назы­вают относительной величиной вредного пространства.

Вследствие наличия вредного пространства произво­дительность компрессора уменьшается.

Величину, характеризующую степень полноты использования рабо­чего объема цилиндра, называют объемным кпд ком­прессора.

 

λ_v = 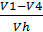.. (160)

Объемный кпд компрессора можно также выразить через относительную величину вредного пространства и отношение давлений нагнетания и всасывания:

λ_v = 1 - а - 1].. (161)

где т — показатель политропы расширения газа, остав­шегося во вредном пространстве.

Теоретическая работа идеального компрессора яв­ляется минимальной. Действительную работу реального компрессора определяют при помощи изотермического или адиабатного кпд и механического кпд:

η_из = ; η_ад =

где l_из и l_{а д} — соответственно теоретическая работа ком­прессора при изотермическом и адиабатном сжатии, а 1_к —действительная работа компрессора. Эти коэффициенты характеризуют степень совершенства действительного про­цесса в сравнении с идеальным.

Механический кпд учитывает механические потери в компрессоре. Произведение изотермического или адиа­батного кпд на механический называют эффективным кпд компрессора η_к.

 

Рисунок 38 – Диаграмма одноступенчатого компрессора

 

Действительная мощность, потребляемая двигателем компрессора, для сжатия М кг/ч газа

С увеличением конечного давления объемный кпд одноступенчатого компрессора уменьшается (рисунок 38), и следовательно, уменьшается также производительность компрессора. В пределе, когда кривая сжатия пересекает линию, характеризующую объем вредного пространства, всасывание воздуха в цилиндр прекращается и, следова­тельно, объемный кпд и производительность компрес­сора становятся равными нулю.

На рисунке 39 и 40 показаны процессы сжатия в двух- и трехступенчатом компрессоре. Линии 1—2, 3—4 и5—6 изображают процесс адиабатного сжатия в каждом ци­линдре компрессора, а линии 2—3 и 4 —5 — процессы изобарного охлаждения воздуха в специальных холо­дильниках.

Процесс сжатия воздуха (газа) в многоцилиндровых или многоступенчатых компрессорах осуществляется по­следовательно во всех цилиндрах с охлаждением воздуха после сжатия в каждом цилиндре. Обычно при этом стре­мятся к тому, чтобы воздух (газ) после холодильника имел ту же температуру, с которой он поступил в предыдущую ступень. Таким образом, для трехступенчатого компрес­сора (рисунок 40)

t₁ = t₃ = t₅

Наиболее выгодным оказывается многоступенчатое сжа­тие в случае, если отношение давлений в каждой ступени принимается одинаковым для всех ступеней.

Рисунок 39 – Процессы сжатия в двухступенчатом компрессоре

Рисунок 40 - Процессы сжатия в трехступенчатом компрессоре

 

Для трехступенчатого компрессора в этом случае

Р₂/Р₁ = Р₄/Р₂ = Р₆/Р₄ = х,

откуда

х = .

или вообще

х = . (162)

 

где х - отношение давлений в каждой ступени;

п - число ступеней компрессора;

р_К - давление воздуха, выходящего из последней ступени;

P₁ - давление воздуха, поступающего в первую сту­пень.

Распределение давлений по формуле (162) приводит к тому, что температуры воздуха на выходе из каждой ступени равны между собой, т. е.

t₂ = t₄ = t_6,

а также к равенству работ всех ступеней. Поэтому для определения работы многоступенчатого компрессора до­статочно найти работу одной ступени и увеличить ее в п раз. -

На рисунке 41 и 42 приведены графики адиабатного и политропного сжатия газа в трехступенчатом компрессоре в диаграмме Ts. Линии 1 — 2, 3 — 4 и 5— 6 изображают процессы сжатия в отдельных цилиндрах, линии 2—3 и 4 — 5 - процессы охлаждения газа при постоянный давлении в первом и втором холодильниках.

 

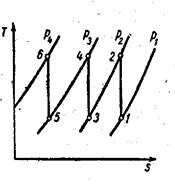
Рисунок 41 – График адиабатного сжатия газа в трехступенчатом компрессоре

 

 

Рисунок 42 - График политропного сжатия газа в трехступенчатом компрессоре

Площади (рисунок 42) 1—2—2'—1', 3-4—4'—3' и 5— 6—6'—5' изображают количество теплоты, отнимаемые от воздуха при политропном его сжатии в отдельных цилиндрах ком­прессора и передаваемые воде, охлаждающей стенки цилиндра.

Площади 2—2' — З'—З и4—4'—5' —5 изображают ко­личества теплоты, отнимаемые от газа при его изобарном охлаждении в первом и втором холодильниках.

Примеры решения задач

1.1 кг воздуха совершает цикл Карно (смотри рисунок 22) в пределах температур t₁= 627° С и t₂ = 27° С, причем наивысшее давление составляет 6 МПа, а наинизшее — 0,1 МПа.

Определить параметры состояния воздуха в характер­ных точках цикла, работу, термический кпд цикла и количество подведенной и отведенной теплоты.

Решение

Точка 1.

Р₁ = 6 МПа; Т₁ = 900 К.

Удельный объем газа находим из характеристического уравнения

V₁= RT₁/Р₁ = 287*900/6*10⁶ = 0,043 м³/кг.

Точка 2.

Т₂ = 900 К.

Из уравнения адиабаты (линия 2—3)

Р₂/Р₃ =() = = 46.8

р₂ = 0,1 *46,8 = 4,68 МПа.

Из уравнения изотермы (линия 1—2)

p₁v₁ = p₂v₂

получаем

V₂ =P₁V₁/Р₂ = 6*0,043/4,68 = 0.055 м³/кг

Точка 3.

р₃ = 0,1 МПа; Т₃ = 300 К;

V₃ = RT3/Р3 = 287*300/0,1*10⁶ = 0,861 м³/кг.

Точка 4.

Т₄ = 300 К.

Из уравнения адиабаты (линия 4 — 1) имеем

Р₁/Р₄ =( = 4,68

Р₄ = Р₁/4,68 = 0,128 МПа.

Из уравнения изотермы (линия3 — 4)получаем

P₃V₃ = P₄V₄

V₄ = P₃*V₃/Р₄ = 0,1*0,861/0,128 = 0,671 м³/кг.

Термический кпд цикла

η_t = Т₁-Т₂/Т₁ = 900 - 300/900 = 0,667

Подведенное количество теплоты

Ϥ₁= RT₁lnV₂|V₁ = 2,303*0,287*900 lg0,055/0,043 = 63,6 кДж/кг.

Отведенное количество теплоты

q₂ = RT₃ lnV₃/V₄= 2,303*0,287*300 lg0,861/0,671= 21,5 кДж/кг.

Работа цикла

l₀ = q₁ - q₂ = 69,6— 21,5 = 42,1 кДж/кг.

Для проверки можно воспользоваться формулой

η_t = q₁ - q₂/ q₁ = l₀/ q₀ = 42,1/63,6 = 0,662.

Ответ: V₁=0,043 м³/кг; р₂ =4,68 Мпа, V₂ = 0.055 м³/кг; V₃ = 0,861м³/кг; Р₄ = 0,128 Мпа, V₄ = 0,671 м³/кг; η_t = 0,667; Ϥ₁= 63,6 кДж/кг, q₂ =21,5 кДж/кг; l₀ = 42,1 кДж/кг.

 

2. Для цикла с подводом теплоты при р = const (рисунок 44) найти параметры в характер­ных точках, полезную работу, термический кпд, количе­ство подведенной и отведен­ной теплоты, если дано: р₁ = = 0,1 МПа; t₁ = 20° С; ε = 12,7; k = 1,4. Рабочее тело — воздух. Теплоемкость считать постоянной.

 

Рисунок 44 – Цикл с подводом теплоты при постоянном давлении

Решение

Точка 1.

P_l = 0,1 МПа; t₁ = 20° С.

Определяем удельный объем:

V₁ = RT₁/Р₁ =287*293/0,1*10⁶ = 0,84 м³/кг

Точка 2.

Так как степень сжатия

ε = V₁/V₂ = 12,7

то

V₂ = V₁/ε = 0,84/12,7 = 0,0661 м³/кг

Температура в конце адиабатного сжатия

Т₂ = Т1( = 293*12,7^0,4 = 293*2,76 = 809 К;

t₂ = 536⁰C

Давление в конце адиабатного сжатия

P₂ = RT₂/V₂ = 287*809/0,0661*10⁶ = 3,51 Мпа

 

Точка 3.

Из соотношения параметров в изобарном процессе

Т₃/Т₂ = V₃/V₂ = P =2

Отсюда

V₃ = V₂P = 0,0661*2 = 0,1322 м³/кг;

Т₃ = Т₂Р = 809*2 = 1618 К; t₃ = 1345⁰С;

Р₃ = Р₂ = 3,51Мпа

 

Точка 4.

V₄ = V₁ = 0.84 м³/кг.

Давление в конце адиабатного расширения

=( ==( = =(

Р₄ = 3,51/13,3 = 0,264 МПа.

Температуру в конце адиабатного сжатия определяем из соотношения параметров в изохорном процессе ( линия4—1);

T₄= T₁ 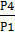= 293*0,264/0,1 = 773 К;

t₄ = 500°С.

Количество подведенной теплоты

Ϥ₁ = ϥ_2-3 = Cp(t₃ –t₂) = 29,3/28,96 (1345 – 536) = 818 кДж/кг

Количество отведенной теплоты (абсолютное значение)

Ϥ₂ = ϥ_4-1 = С_v(t₄ – t₁) = 20,97/28,96 (500-20) = 347 кДж/кг

Термический кпд цикла

η_t = ϥ₁ – ϥ₂/ϥ₁ = 818 – 347/818 = 0,576 = 57,6%.

Работа цикла

l₀ = ϥ₁ – ϥ₂ = 818- 347 = 471 кДж/кг.

Ответ: V₁ = 0,84 м³/кг; ε =12,7; V₂ =0,0661 м³/кг; Т₂ = 809 К; P₂ = 3,51 Мпа; V₃ = 0,1322 м³/кг; Т₃ = 1618 К; Р₃ = Р₂ = 3,51Мпа; Р₄ = 0,264 Мпа; T₄=773 К; Ϥ₁ = 818 кДж/кг; Ϥ₂ = 347 кДж/кг η_t = 57,6%; l₀ = 471 кДж/кг.

 

⇐ Предыдущая6789101112131415Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: