 |
Прямые однократные и косвенные измерения, и их погрешности
|
|
|
|
Истинное значение измеряемой величины определить невозможно прежде всего потому, что ограничено воспроизведение эталона единицы физической величины. Пример, эталон килограмма воспроизводится с точностью 2∙10-9 кг.; температуру тройной точки воды удаётся поддерживать со стандартным отклонением 2∙10-4К, чем и определяется стандартное отклонение воспроизведения кельвина, составляющее примерно 10-3К; скорость света, являющаяся основной для реализации эталонов метра и секунды, также измерены с некоторой погрешностью, истинное значение скорости света находится в интервале 299792458,8 м/с < c < 299792459,2 м/с; диапазон временных интервалов, воспроизводимых эталоном времени, составляет 10-9...108с.
За наиболее достоверное значение непосредственно измеряемой физической величины 
принимают среднее арифметическое X ср из всех n результатов её измерений 
: 
.
Окончательный результат измерения величины представляют в форме:
,
где 
- положительная величина, называемая абсолютной погрешностью найденного значения .
В каждом измерении возможно определить границу абсолютной погрешности измерения, как половина длины интервала 2∆ X от 
до 
, достоверно содержащего истинное значение измеряемой величины. С вероятностью, близкой к единице, интервал длиной 2∆ X содержит все возможные значения погрешности измерений.
Граница абсолютной погрешности представляет собой доверительный интервал 
- это интервал, в котором находится истинное значение измеряемой величины 
.
Граница абсолютной погрешности не в полной мере характеризует измерение. Для этого вводят границу относительной погрешности.
Относительной погрешностью значения называется отношение
|
|
|
.
Надежностью полученного результата измерения физической величины 
называется вероятность Р того, что истинное значение действительно лежит в интервале от до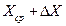 
.
Способ определения значения измеряемой физической величины и граница абсолютной погрешности измерения 
зависят от вида измерений.
При выполнении многих экспериментов результаты прямых измерений при проведении опытов в неизменных условиях изменяются случайным образом, и отличие между этими результатами превышает границу погрешности 
. При этом возникают две проблемы:
1 - если при каждом измерении получается новый результат, то какой из них следует принять в качестве приближённого значения измеряемой величины?
2 – как оценить границу случайной погрешности измерений?
Случайные погрешности подчиняются нормальному распределению (распределению Гаусса) — распределение вероятностей, которое играет важнейшую роль во многих областях знаний, особенно в физике. Физическая величина подчиняется нормальному распределению, когда она подвержена влиянию огромного числа случайных помех.
Анализ распределения Гаусса позволил выдвинуть «принцип арифметической середины», согласно которому при бесконечном увеличении числа опытов n в серии среднее арифметическое результатов стремится к истинному значению Хист: Хср→Хист; n→∞
Теоретические исследования позволили получить правило «трёх сигма (3σ)». Оно утверждает, что при очень большом числе n опытов в серии 99,7% всех результатов оказывается в интервале [μ±3σ], где σ – стандартное отклонение.
В серии n опытов за результат измерений принимается среднее арифметическое значение:
.
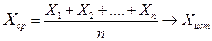При числе измерений 
с надёжностью Р≈2/3 можно принять, что абсолютная погрешность 
равна стандартной (среднеквадратичной) погрешности, граница случайных погрешностей принимается примерно равной 3σ:
|
|
|
(1)
С увеличением n стандартная погрешность Δ Хкв уменьшается (при больших значениях n погрешность 
). Поэтому точность результата измерений, лимитируемая случайными погрешностями, растёт с увеличением числа измерений.
Надёжность результата серии измерений n – это вероятность 
того, что истинное значение измеряемой величины 
попадает в данный доверительный интервал. За вероятность появления величины в интервале 
принимают отношение числа 
тех результатов измерения, которые попадают в этот интервал, к общему числу 
произведённых измерений 
: 
.
Надёжность выражается или в долях единицы, или в процентах.
Величина надёжности 
будет зависеть от числа n произведённых измерений, а так же от величины задаваемой погрешности.
Производя большое число измерений, можно сузить ширину доверительного интервала при той же надёжности. Однако это увеличивает трудоёмкость измерений и снижает производительность труда экспериментаторов. Поэтому можно ограничить число необходимых измерений за счёт разумного подхода к ширине доверительного интервала. Но при ограниченном числе измерений квадрат эмпирического стандарта будет случайной величиной и в лучшем случае определяет лишь порядок дисперсии ошибки. Поэтому для оценки границ доверительного интервала приходится вводить дополнительный коэффициент 
. Этот коэффициент был предложен в 1908 году английским математиком и химиком В.С. Госсетом, публиковавшим свои работы под псевдонимом «Стьюдент», и получил впоследствии название коэффициента Стьюдента. Значения коэффициента Стьюдента для разных значений надежности α при разных значениях числа измерений приводится в таблице 1.
Если необходимо повысить надежность Р результата, то значение 
следует соответственно увеличить.
Таким образом, величина абсолютной погрешности определяется:
(2)
где – положительный коэффициент, зависящий от n и Р.
Результат серии измерений можно записать:
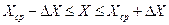или 
.
Это означает, что истинное значение величины 
попадает в доверительный интервал 
с надежностью, равной 
.
Относительная погрешность измерений, проведенных с надежностью 
, равна:
|
|
|
(3)
В общем случае необходимо принимать во внимание как случайные, так и систематические погрешности прямых измерений.
В этом случае для повышения точности результата измерений нет смысла увеличивать число измерений, а нужно принять меры к уменьшению систематической погрешности (например, использовать более точные приборы).
Стандартная систематическая погрешность оценивается на основе анализа метода измерения и используемых средств измерения. Все систематические погрешности, поддающиеся исключению (например, некоторые методические погрешности), должны быть устранены ещё до начала обработки экспериментальных данных путём введения к ним соответствующих поправок. Именно эти исправленные значения 
и рассматриваются как исходные экспериментальные данные при отыскании 
и доверительного интервала.
Погрешность прямых измерений связана прежде всего с основными погрешностями мер и измерительных приборов (инструментальными). Процедура определения основной погрешности меры или прибора называется поверкой. Она состоит в сравнении показаний рабочего прибора с показаниями образцового прибора на заводе - изготовителя.
Инструментальная (приборная) погрешность определяется на основе паспортных данных прибора, его класса точности, точности нониуса и т.д.
Для большинства измерительных приборов инструментальная погрешность задаётся при помощи числа, называемого классом точности.
Классом точности средства измерения называется характеристика последнего, служащая показателем установленных для него государственным стандартом пределов погрешностей и других параметров, влияющих на точность.
Пример, если основная погрешность прибора не превышает ±2,5% предела измерения, то число 2,5 и есть класс точности прибора. Зная класс точности прибора, легко найти границу абсолютной основной погрешности прибора Δпр:
.
Пример, для амперметра с пределом измерения 2 А и классом точности γ=0,5, получим:
.
Многие показывающие приборы (манометры, амперметры, вольтметры и др.) нормируются по приведённой погрешности – погрешности, выраженной в процентах от верхнего предела измерений (у многопредельных приборов – от верхнего предела на соответствующем диапазоне), или от длины шкалы. Применяются следующие классы точности таких приборов: 0,1; 0,2; 0,5; 1,0; 1,5; 2,5; 4,0. Класс точности обозначается на шкале приборов числом в кружке (см. рисунок).
|
|
|
Измерительные приборы могут также нормироваться по относительной погрешности – погрешности, выраженной в процентах от действительного значения измеряемой величины.
Если класс точности прибора не указан и в паспорте прибора нет данных относительно его инструментальной погрешности, то обычно считают, что эта погрешность равна половине цены наименьшего деления шкалы прибора. В случае прибора, стрелка которого перемещается не равномерно, а «скачками» (например, у ручного секундомера), приборную погрешность считают равной цене деления шкалы.
При записи результата измерений в стандартной форме необходимо соблюдать следующие правила:
1 - величину погрешности 
необходимо округлить до двух значащих цифр, если первая из них – единица или двойка, и до одной значащей цифры во всех остальных случаях;
2 - при записи значения необходимо указывать все цифры вплоть до последнего разряда, использованного для записи погрешности.
При оценке границ погрешностей косвенных измерений необходимо отыскать связь между видом функции 
, связывающей искомую величину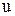 
с величинами 
, измеренными непосредственно, и границами погрешностей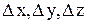 
.
Для определения границ погрешностей косвенных измерений используется методика нахождения абсолютной погрешности с использованием дифференциала функции (см. пункт 3 Введение).
|
|
|
