 |
Лабораторная работа № 5 Изучение законов колебания физического маятника
|
|
|
|
Цель работы: Изучение закона колебаний физического маятника при малых углах отклонения и экспериментальное подтверждение формулы периода колебаний физического маятника.
Приборы и материалы: прибор для определения моментов инерции; набор физических маятников: однородный диск, стержень, обруч; штангенциркуль; секундомер.
Задание:
1. Для выполнения лабораторной работы необходимо ознакомиться с теорией и порядком выполнения работы.
2. С помощью набора физических маятников определить момент инерции тел и подтвердить формулу периода колебаний физического маятника.
3. Найдите самостоятельно моменты инерции 
для однородного диска и обруча, приведённых на рисунке 4.
4. Оценить погрешность измерений периодов колебаний физических маятников полученных теоретическим и экспериментальным путём.
5. По результатам обработки теоретических и экспериментальных данных сделать вывод.
6. После выполнения лабораторной работы, ответить на контрольные вопросы.
ТЕОРИЯ
I. Колебания и волны – наиболее распространённый вид движения. Не существует такого уровня организации материи (поля, частиц, молекулы, атома и т.д), на котором не проявлялись бы колебательные процессы. Знания законов, управляющих колебательно-волновыми процессами в природе и технике, для инженеров является чрезвычайно важным.
Колебаниями называются процессы, отличающиеся той или иной степенью повторяемости во времени.
Подобные процессы наблюдаются в системах разной физической природы.
В зависимости от характера воздействия на колеблющуюся систему различают свободные (собственные) колебания, вынужденные колебания, автоколебания, параметрические колебания.
|
|
|
1) Свободными (собственными) колебаниями называются колебания, которые происходят в системе, предоставленной самой себе после выведения из положения равновесия. Колебания происходят с одинаковой амплитудой, и предполагается, что в этом случае подводимая энергия сохраняется. Пример: колебания шарика, подвешенного на нити (маятник); колебания груза, подвешенного на пружине в поле тяготения.
2) Вынужденными колебаниями называются колебания, в процессе которых колеблющаяся система подвергается воздействию внешней периодически изменяющейся силы. Пример: колебания моста, возникающие при прохождении по нему людей, шагающих в ногу; звуковая волна, распространяющая в среде, где имеется источник звука; электромагнитные колебания в контуре, куда включена периодическая ЭДС.
3) Автоколебания сопровождаются воздействием на колеблющуюся систему внешних сил, однако моменты времени, когда осуществляются эти воздействия, задаются самой колеблющейся системой – система сама управляет внешним воздействием. Пример: механические и электронные часы.
4) Параметрическими колебаниями называются колебания, в которых за сч ё т внешнего воздействия происходит периодическое изменение какого-либо параметра системы. Пример: изменение длины нити, к которой подвешен шарик, совершающий колебания; изменение массы груза или пружины в пружинном маятнике.
5) Простейшими являются гармонические колебания – колебания, при которых колеблющаяся величина (отклонение маятника, скорость, ускорение, сила) изменяется со временем по закону синуса или косинуса. Этот вид колебаний особенно важен по следующим причинам:
ü колебания в природе и технике часто имеют характер, очень близкий к гармоническим колебаниям;
ü периодические процессы иной формы (с другой зависимостью от времени) могут быть представлены как наложение нескольких гармонических колебаний.
|
|
|
Гармонические колебания можно представить в виде проекции равномерного движения по окружности. Если изобразить графически колебания на диаграмме отклонение – время, то получится синусоидальная кривая. Поэтому, часто гармонические колебания называются синусоидальными колебаниями.
При прохождении положения равновесия, то есть, положения, которое занимает покоящаяся система, колеблющееся тело имеет наибольшую скорость; в точке максимального отклонения (точка поворота) скорость равна нулю.
II. Физическим маятником называется любое тв ё рдое тело, способное под действием силы тяжести совершать колебания вокруг точки подвеса, не проходящей через его центр масс (центр тяжести).
На рисунке 1 изображено сечение физического маятника плоскостью, перпендикулярной оси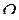 
и проходящей через центр масс 
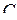. Расстояние от оси колебания до центра масс (тяжести) обозначим через 
.
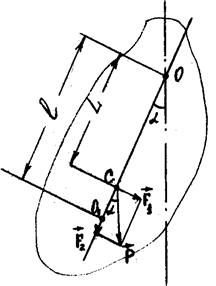
Рис унок 1 - С ечение физического маятника плоскостью, перпендикулярной оси 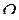и проходящей через центр масс 
.
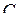Отклоним маятник от положения равновесия на небольшой угол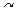 
. Разложим силу тяжести 
на две составляющие: 
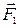, перпендикулярную 
, и 
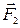, направленную по .
Составляющая 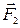уравновешена реакцией оси 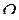, а составляющая 
стремится возвратить маятник в положение равновесия. При малых углах отклонения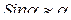 
, измеренному в радианах, составляющая 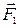равна:
.
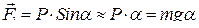Сила 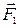прямо пропорциональна 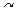(угловому смещению) и направлена к положению равновесия. Силы, имеющие такой характер, называются неупругими. Она создаёт момент силы относительно оси :
,
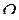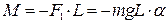где - плечо силы 
относительно оси 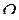. Знак минус указывает, что момент силы всегда стремится вернуть маятник в положение равновесия.
По основному закону динамики вращательного движения имеем:
,
где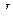 
- момент инерции тела,
- угловое ускорение.
Применим данный закон к нашему случаю:
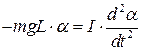
или 
. (1)
Это дифференциальное уравнение в неявном виде выражает зависимость угла отклонения маятника от положения равновесия от времени. Чтобы получить эту зависимость в явном виде, нужно решить это уравнение. Зная, что процесс движения периодический, решение будем искать в виде:
|
|
|
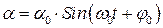. (2)
Убедимся, что такой вид зависимости 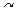от времени удовлетворяет уравнению (1). Возьмём вторую производную по времени от уравнения (2). Получим:
. (3)
Подставим (2) и (3) в (1). Получим:
.
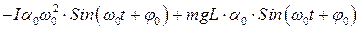Откуда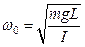 
. (4)
Т.е., чтобы уравнение (2) было решением уравнения (1) необходимо, чтобы 
в уравнении (2) была выбрана так, чтобы выполнялось равенство (4).
Остановимся подробнее на уравнении (2). Как видно из уравнения, угол 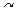меняется со временем по синусоидальному закону.
Когда какая-либо физическая величина колеблется по такому закону, то колебания называются гармоническими, а само уравнение (2) – уравнением гармонического колебания.
Разберёмся в физическом смысле констант 
, входящих в уравнение (2).
Так как максимальное значение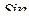 
равно единице, то 
.
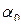- амплитуда колебания, т.е. максимального смещения от положения равновесия;
- круговая или циклическая частота: связь с обычной частотой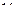 
даётся равенством 
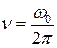; или через период 
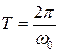. (5)
С учётом этого, уравнение (2) можно переписать в виде:
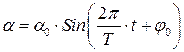
или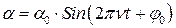 
,
- период колебания или время одного полного колебания;
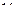- частота колебания или число полных колебаний в единицу времени.
Величина, стоящая под знаком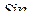 
- называется фазой колебания. Она имеет размерность угла, но не является углом в обычном смысле слова, его нельзя указать при движении маятника.
Если положить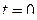 
, то фаза окажется равной 
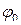, поэтому 
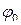называют начальной фазой.
Перепишем (4) с учётом (5):
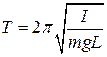, (6)
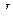- момент инерции маятника относительно оси колебания 
;
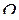- масса маятника;
- ускорение свободного падения.
Период колебания физического маятника прямо пропорционален корню квадратному из его момента инерции и обратно пропорционален корню квадратному из его массы и расстояния от оси колебания до центра тяжести.
В выражении периода отсутствует 
, следовательно, при малых углах 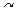период колебания физического маятника не зависит от амплитуды.
Период колебания можно подсчитать по формуле (6), зная геометрические размеры и форму маятника. С другой стороны его можно определить опытным путём. Для этого нужно измерить время нескольких колебаний и, разделив время 
на число колебаний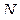 
, получить период колебаний: 
.
|
|
|
Совпадение (в пределах погрешности измерений) периодов, определённых тем и другим способом, служит подтверждением правильности приведённой теории. Такая методика и использована в данной работе.
|
|
|
