 |
Порядок выполнения лабораторной работы
|
|
|
|
1. Преобразовать формулу (6) периода колебаний физического маятника
к удобному для расчётов виду (выразив при этом 
(с помощью теоремы Штейнера) и 
через характерный размер маятника: для стержня – это длина, для диска – радиус, для кольца – средний радиус).
2. Измерить характерные размеры маятников не менее 3-х раз и результаты занести в таблицу 1.
3. Определить периоды маятников по расчётным формулам и результаты занести в таблицу 1.
Таблица 1 – Нахождение периода колебаний теоретическим путём
| № п/п | Стержень | Диск | Кольцо | |||
| L, м | T, с | R, м | T, с | Rср, м | Т, с | |
| 1 | ||||||
| 2 | ||||||
| 3 | ||||||
| 
| 
|
|  =
|
| |
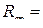
4. Поочередно определить периоды маятников экспериментально по формуле: 
, где 
- время колебаний маятников,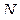 
- число колебаний.
5. Данные измерений и вычислений занести в таблицу 2.
Таблица 2 - Нахождение периода колебаний экспериментальным путём
|
№ п/п |
N | Стержень | Диск | Кольцо | |||
| t, с | T, с | t, с | T, с | t, с | T, с | ||
| 1 | 50 | ||||||
| 2 | 50 | ||||||
| 3 | 50 | ||||||
|
| 
|
| 
|
| ||
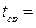
6. Оценить результаты экспериментальных и теоретических значений путём подсчёта 
по формуле:
.
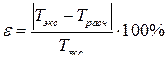Контрольные вопросы:
1. Что называется вращательным и колебательным движением.
2. Момент силы. Момент инерции твёрдого тела. Теорема Штейнера.
3. Основной закон динамики вращательного движения. Его выражение для движения физического маятника под действием силы тяжести.
4. Гармонические колебания. Величины, характеризующие гармонические колебания.
|
|
|
5. Колебания математического и физического маятников. Периоды колебаний. Приведённая длина физического маятника.
Литература:
1. Савельев И.В. Курс общей физики (в 3-х томах): учебное пособие для вузов/ И.В. Савельев. – 4-е-11-е изд. – СПб: Лань, 2003-2011. Т1-432с. Т2-496с. Т3-317с.
2. Детлаф А.А., Яворский Б.М. Курс физики: учебное пособие для втузов – 7-е изд., стер. - М.: Academa, 1999-2003 г. -720с.
3. Трофимова Т.И. Курс физики: учебное пособие. – 4-е-11-е изд.-М.: Высш.шк., 203-2011. – 542с.
4. Курс физики: Учебник для вузов: в 2-х томах/ под ред. В.Н. Лозовского. – 2-е изд.- СПб.: Лань, 2001. Т1-576с. Т2-592с.
5. Яворский Б.М. Справочник по физике/ Б.М. Яворский, А.А. Детлаф – 1-е-4-е изд. Перераб. и доп. – М.: Наука, 1980-1996. – 624с.
6. А.В. Корнев, Ю.В. Рублев. Практикум по физике.
Лабораторная работа № 6 Определение коэффициента вязкости по методу Стокса
Цель работы: Определить динамический коэффициент вязкости глицерина по методу Стокса.
Приборы и материалы: цилиндр с исследуемой жидкостью, микрометр, секундомер, металлические шарики.
Задание:
1. Для выполнения лабораторной работы необходимо ознакомиться с теорией и порядком выполнения работы.
2. Определить динамический и кинематический коэффициент вязкости глицерина сравнить с и табличным значением при данной температуре.
3. Оценить погрешность измерений динамического коэффициента вязкости глицерина полученным экспериментальным путём.
4. По результатам обработки теоретических и экспериментальных данных сделать вывод.
5. После выполнения лабораторной работы, ответить на контрольные вопросы.
ТЕОРИЯ
Гидро- и аэродинамика – раздел механики сплошных сред, занимающийся изучением законов движения несжимаемых жидкостей и газов, а так же взаимодействие несжимаемых жидкостей с тв ё рдыми телами.
Всем реальным жидкостям и газам в большей или меньшей степени присуща вязкость или внутреннее трение.
|
|
|
Вязкость жидкостей – это свойство, благодаря которому выравниваются скорости движения различных слоев жидкости.
Существует два вида течения вязкой жидкости или газа.
Если жидкость разделить на слои, то они будут скользить относительно друг друга не перемешиваясь. Течение жидкостей при наличии внутреннего трения, но не сопровождающееся образованием вихрей, называется ламинарным течением (от лат. lamina - пластинка, полоска). Ламинарное течение стационарно.
При увеличении скорости или поперечных размеров потока характер течения изменяется. Происходит перемешивание жидкости, возникают вихри, а следовательно, и силы, препятствующие течению. Такое течение называется турбулентным течением (от лат. turbulentus — бурный, беспорядочный). Сопротивление потоку, сила, действующая на помещенное в поток тело, складывается из разности давлений перед и за телом и силы трения на поверхности тела. Турбулентность экспериментально открыта английским инженером Рейнольдсом в 1883 году при изучении течения воды в трубах.
Рейнольдс установил, что характер течения зависит от значения безразмерной величины:
,
где Re – число Рейнольдса;
– характерные размеры тела (радиус шара, радиус трубы, сторона квадрата при квадратном сечении;
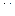- скорость тела относительно среды или средняя (по сечению трубы) скорость потока;
- динамическая вязкость;
- кинематическая вязкость;
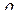- плотность текущей среды.
При малой скорости (при малом числе Рейнольдса), течение любой жидкости или газа будет ламинарным. Если скорость возрастает и достигает критического значения 
(соответствующее число Рейнольдса 
), то ламинарное течение сменяется турбулентным, гидравлическое сопротивление значительно увеличивается.
Из формулы следует, что число Рейнольдса не изменится, если уменьшить размеры тела и соответственно увеличить скорость потока или уменьшить вязкость среды.
Закон подобия: коэффициенты геометрически подобных тел равны, если равны соответствующие числа Рейнольдса. В этом случае оба потока подобны.
· Этот закон даёт возможность проводить экспериментальное исследование сложных процессов, используя модели обтекаемых тел.
· Число Рейнольдса может служить критерием подобия для течения жидкостей в трубах, каналах и т.д. Характер течения различных жидкостей (газов) в трубах разных сечений будет совершенно одинаков, если каждому течению соответствует одно и то же значение Re.
|
|
|
Сила вязкости обусловлена обменом молекулами между соседними элементами объ ё ма жидкости, при котором скорости этих элементов уравниваются.
Эта сила возникает только в текущей жидкости. Природу возникновения силы вязкости можно объяснить молекулярным строением жидкости. Выравнивание скоростей соседних слоёв жидкости, если эти скорости различны, происходит благодаря тому, что из слоя жидкости с большей скоростью движения переносится импульс (количество движения) к слою, движущемуся с меньшей скоростью.
При ламинарном течении отдельные слои жидкости движутся с различными скоростями. Непосредственно у стенки скорость течения жидкости равна нулю, а на оси трубы максимальна. Скорости разных слоёв распределены так, как показано на рисунке 1, где стрелки представляют векторы скорости жидкости.
Рис унок 1 – Распределение скоростей слоёв жидкости
Наибольшая скорость наблюдается в средней части трубы, по мере приближения к стенкам скорость уменьшается, а слой, непосредственно прилегающий к стенкам трубы, покоится. При таком течении происходит перенос импульса от центрального слоя жидкости, где скорость наибольшая, к слоям, движущимся с меньшей скоростью.
Опишем количественно перенос импульса. Пусть изменение скорости жидкости происходит в направлении оси 
, которое в данном случае перпендикулярно направлению самой скорости движения жидкости (рис. 2).
Рис унок 2 – Изменение скорости слоёв жидкости в направлении оси .
В направлении, перпендикулярном оси , направление скорости движения во всех точках одинаково. Это значит, что скорость 
является функцией только . Тогда, как показывает опыт, количество движения 
, переданное за 
секунд площадке 
сечения, перпендикулярного оси , определяется уравнением:
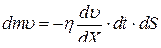, (1)
где 
- градиент скорости вдоль оси , характеризующий быстроту изменения скорости вдоль оси (изменение скорости на каждую единицу длины).
|
|
|
Знак «минус» означает, что импульс переносится в направлении уменьшения скорости. При переносе импульса от слоя к слою происходит изменение импульса этих слоев (увеличение или уменьшение). Это значит, что на каждый из слоёв действует сила, равная изменению импульса в единицу времени (второй закон Ньютона).
Уравнение (1) можно записать в виде:
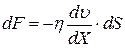(2/)
, (2)
где 
- сила, действующая на поверхности слоя.
Во всех реальных жидкостях при перемещении одних слоёв относительно других возникают более или менее значительные силы трения. Со стороны слоя, движущегося более быстро, на слой, движущийся медленнее, действует ускоряющая сила. Наоборот, по третьему закону Ньютона, со стороны слоя, движущегося медленнее, на более быстрый слой действует задерживающая сила. Эти силы носят название сил внутреннего трения. Они направлены по касательной к поверхности слоёв.
Коэффициент пропорциональности 
называется коэффициентом динамической вязкости или коэффициентом внутреннего трения и зависит от свойств жидкости. Физический смысл коэффициента динамической вязкости заключается в том, что он численно равен силе внутреннего трения, действующей на 1 м2, при градиенте скорости равном единице.
В системе СИ единица коэффициента динамической вязкости определяется как коэффициент вязкости такой жидкости (или газа), в который при градиенте скорости равном 1 с-1 на 1 м2 площади слоя действует сила в 1 Н. В системе СИ эта единица называется Паскаль секунда (Па·с).
Коэффициент вязкости зависит от температуры, характер этой зависимости различен для жидкостей и газов. У жидкостей коэффициент вязкости сильно уменьшается с повышением температуры. У газов, коэффициент вязкости с температурой растет. Это связано с различием механизма внутреннего трения в жидкостях и газах.
Кроме понятия динамической вязкости применяются понятия текучести и кинематической вязкости.
Текучестью называется величина, обратная динамической вязкости:
(1/Па∙с).
Кинематической вязкостью называется отношение динамической вязкости к плотности среды:
(м2/с).
В данной работе коэффициент динамической вязкости определяется методом, предложенным Стоксом. При движении тела в вязкой среде возникает сопротивление. При малых скоростях и обтекаемой форме тела, когда не возникает вихрей, сила сопротивления непосредственно обусловлена вязкостью жидкости. Слой жидкости, непосредственно прилегающий к твёрдому телу, прилипает к его поверхности и увлекается им полностью. Следующий слой увлекается за телом с меньшей скоростью, таким образом между слоями возникают силы трения. В этом случае сила сопротивления по закону, установленному Стоксом, прямо пропорциональна первой степени скорости, коэффициенту трения и линейным размерам тела. Таким образом, в предположении, что жидкость обтекает шар ламинарно и радиус шара намного меньше размеров сосуда, действует сила сопротивления, то движение шара можно описать законом Стокса:
|
|
|
, (3)
где - динамическая вязкость;
- радиус шара;
- скорость шара относительно жидкости.
|
|
|
