|
Порядок выполнения лабораторной работы
|
|
|
|
1. Установить стойку прибора в вертикальное положение, используя математический маятник в качестве отвеса.
2. Подвесить деталь для колебаний около оси 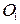 . Измерить время
. Измерить время 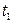 , за которое совершается «
, за которое совершается «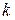 » малых колебаний (
» малых колебаний (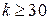 ).
).
Опыт повторить не менее 5 раз.
3. Определить период колебаний 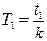 , где
, где 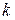 - число полных колебаний.
- число полных колебаний.
4. С помощью математического маятника проверить, действительно ли расстояние 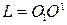 является приведённой длиной физического маятника (детали), колеблющегося около оси
является приведённой длиной физического маятника (детали), колеблющегося около оси 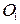 .
.
5. Измерить расстояние 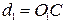 .
.
6. Данные измерений и дальнейших вычислений занести в таблицу.
7. Вычислить по формуле (13) момент инерции 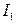 детали относительно оси
детали относительно оси 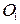 .
.
8. Аналогичным образом (пункты 2, 3, 5) определить момент инерции 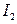 детали относительно оси
детали относительно оси  . Убедиться, что моменты инерции детали действительно разные (в зависимости от выбора оси инерции).
. Убедиться, что моменты инерции детали действительно разные (в зависимости от выбора оси инерции).
9. По формуле (14) определить момент инерции детали с учётом приведённой длины физического маятника 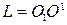 .
.
10. Вычислить среднее значение периодов колебаний (прямое измерение) Т1 и Т2, а также абсолютную и относительную погрешность прямого измерения, при надёжности 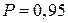 (см. лабораторная работа №1).
(см. лабораторная работа №1).
11. Рассчитать погрешности косвенных измерений момента инерции экспериментальным (формула 13) и теоретическим (формула 14) путём при надёжности 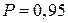 (см. лабораторная работа №1).
(см. лабораторная работа №1).
Таблица
|
| ||||||
| № изм. | Колебания около оси | Колебания около оси | ||||
| k | 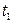
| 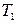
| k | 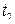
| 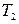
| |
| 1. | ||||||
| 2. | ||||||
| 3. | ||||||
| 4. | ||||||
| 5. | ||||||
3(а): 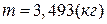 ; 3(б):
; 3(б): 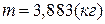 .
.
Контрольные вопросы:
1. Что называется вращательным и колебательным движением.
|
|
|
2. Момент инерции тела. Теорема Штейнера.
3. Математический и физический маятники.
4. Момент силы, действующий на маятник, отклонённый от положения равновесия.
5. Основной закон динамики вращательного движения для физического маятника.
6. Закон движения физического маятника.
7. Период колебаний математического и физического маятника.
8. Приведённая длина физического маятника.
9. Определение момента инерции тела методом колебаний.
Литература:
1. Савельев И.В. Курс общей физики (в 3-х томах): учебное пособие для вузов/ И.В. Савельев. – 4-е-11-е изд. – СПб: Лань, 2003-2011. Т1-432с. Т2-496с. Т3-317с.
2. Детлаф А.А., Яворский Б.М. Курс физики: учебное пособие для втузов – 7-е изд., стер. - М.: Academa, 1999-2003 г. -720с.
3. Трофимова Т.И. Курс физики: учебное пособие. – 4-е-11-е изд.-М.: Высш.шк., 203-2011. – 542с.
4. Курс физики: Учебник для вузов: в 2-х томах/ под ред. В.Н. Лозовского. – 2-е изд.- СПб.: Лань, 2001. Т1-576с. Т2-592с.
5. Яворский Б.М. Справочник по физике/ Б.М. Яворский, А.А. Детлаф – 1-е-4-е изд. Перераб. и доп. – М.: Наука, 1980-1996. – 624с.
6. А.В. Корнев, Ю.В. Рублев. Практикум по физике.
Лабораторная работа № 4 Определение ускорения свободного падения оборотным маятником
Цель работы: опираясь на свойства обратимости точек подвеса и центра качания физического маятника определить ускорение свободного падения тел, используя оборотный маятник.
Приборы и материалы: оборотный маятник, секундомер, линейка.
Задание:
1. Для выполнения лабораторной работы ознакомиться с теорией и порядком выполнения работы.
2. С помощью оборотного маятника определить ускорение свободного падения.
3. Определить абсолютную и относительную погрешность прямых и косвенных измерений.
4. По результатам обработки экспериментальных данных сделать вывод.
5. После выполнения лабораторной работы, ответить на контрольные вопросы.
ТЕОРИЯ
В данной работе для определения ускорения свободного падения (или ускорения силы тяжести) рассматриваются колебательные движения (свободные колебания) и используется так называемый оборотный физический маятник.
|
|
|
I. Колебания и волны – наиболее распространённый вид движения. Не существует такого уровня организации материи (поля, частиц, молекулы, атома и т.д), на котором не проявлялись бы колебательные процессы. Знания законов, управляющих колебательно-волновыми процессами в природе и технике, для инженеров является чрезвычайно важным.
Колебаниями называются процессы, отличающиеся той или иной степенью повторяемости во времени.
Подобные процессы наблюдаются в системах разной физической природы.
В зависимости от характера воздействия на колеблющуюся систему различают свободные (собственные) колебания, вынужденные колебания, автоколебания, параметрические колебания.
1) Свободными (собственными) колебаниями называются колебания, которые происходят в системе, предоставленной самой себе после выведения из положения равновесия. Колебания происходят с одинаковой амплитудой, и предполагается, что в этом случае подводимая энергия сохраняется. Пример: колебания шарика, подвешенного на нити (маятник); колебания груза, подвешенного на пружине в поле тяготения.
2) Вынужденными колебаниями называются колебания, в процессе которых колеблющаяся система подвергается воздействию внешней периодически изменяющейся силы. Пример: колебания моста, возникающие при прохождении по нему людей, шагающих в ногу; звуковая волна, распространяющая в среде, где имеется источник звука; электромагнитные колебания в контуре, куда включена периодическая ЭДС.
3) Автоколебания сопровождаются воздействием на колеблющуюся систему внешних сил, однако моменты времени, когда осуществляются эти воздействия, задаются самой колеблющейся системой – система сама управляет внешним воздействием. Пример: механические и электронные часы.
4) Параметрическими колебаниями называются колебания, в которых за сч ё т внешнего воздействия происходит периодическое изменение какого-либо параметра системы. Пример: изменение длины нити, к которой подвешен шарик, совершающий колебания; изменение массы груза или пружины в пружинном маятнике.
|
|
|
5) Простейшими являются гармонические колебания – колебания, при которых колеблющаяся величина (отклонение маятника, скорость, ускорение, сила) изменяется со временем по закону синуса или косинуса. Этот вид колебаний особенно важен по следующим причинам:
ü колебания в природе и технике часто имеют характер, очень близкий к гармоническим колебаниям;
ü периодические процессы иной формы (с другой зависимостью от времени) могут быть представлены как наложение нескольких гармонических колебаний.
Гармонические колебания можно представить в виде проекции равномерного движения по окружности. Если изобразить графически колебания на диаграмме отклонение – время, то получится синусоидальная кривая. Поэтому, часто гармонические колебания называются синусоидальными колебаниями.

При прохождении положения равновесия, то есть, положения, которое занимает покоящаяся система, колеблющееся тело имеет наибольшую скорость; в точке максимального отклонения (точка поворота) скорость равна нулю.
II. Физическим маятником называется любое тв ё рдое тело, способное под действием силы тяжести совершать колебания вокруг точки подвеса, не проходящей через его центр масс (центр тяжести).
При отклонении маятника от положения равновесия на угол 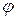 (рис. 1) возникает вращающий момент
(рис. 1) возникает вращающий момент 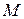 , стремящийся возвратить маятник в положение равновесия.
, стремящийся возвратить маятник в положение равновесия.
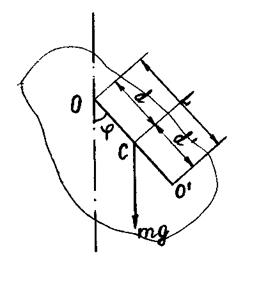
Рис унок 1 – Физический маятник
Этот момент равен:
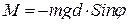 , (1)
, (1)
где 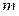 - масса маятника,
- масса маятника,
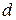 - расстояние между точкой подвеса и центром масс маятника.
- расстояние между точкой подвеса и центром масс маятника.
На основании основного закона динамики для вращательного движения можно записать (без учёта сил трения):
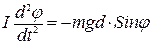 , (2)
, (2)
где 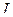 - момент инерции маятника относительно оси вращения.
- момент инерции маятника относительно оси вращения.
В случае малых колебаний 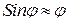 , и выражение (2) принимает вид:
, и выражение (2) принимает вид:
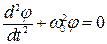 (3)
(3)
где 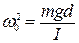 . (3/)
. (3/)
Решением дифференциального уравнения (3) является выражение:
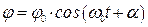 (4)
(4)
где  - амплитуда колебаний;
- амплитуда колебаний;
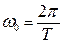 - круговая или циклическая частота колебания (число колебаний за
- круговая или циклическая частота колебания (число колебаний за 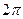 сек);
сек);
|
|
|
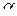 - начальная фаза.
- начальная фаза.
В том, что выражение (4) действительно является решением уравнения (3) легко убедиться, подставив (4) в (3). Из уравнения (4) следует, что при малых отклонениях от положения равновесия и отсутствии трения физический маятник совершает гармонические колебания.
Так как 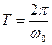 , то в соответствии с (3) период колебаний физического маятника равен:
, то в соответствии с (3) период колебаний физического маятника равен:
 . (5)
. (5)
Формула (5) показывает, что период, а, следовательно, и частота колебания физического маятника при малых колебаниях и отсутствии трения существенно зависит не только от расстояния от оси вращения до центра тяжести, но и от распределения отдельных элементов массы маятника, характеризуемого отношением 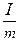 . Как и для математического маятника период колебаний физического маятника не зависит от амплитуды колебаний. Формулу (5) можно переписать так:
. Как и для математического маятника период колебаний физического маятника не зависит от амплитуды колебаний. Формулу (5) можно переписать так:
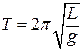 , (6)
, (6)
где 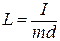 (7)
(7)
является приведённой длиной физического маятника.
 Приведённой длиной физического маятника называется длина такого математического маятника, циклическая частота (период) колебаний которого совпадает с циклической частотой (периодом) данного физического маятника.
Приведённой длиной физического маятника называется длина такого математического маятника, циклическая частота (период) колебаний которого совпадает с циклической частотой (периодом) данного физического маятника.
Точка 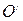 , лежащая на прямой ОС на расстоянии
, лежащая на прямой ОС на расстоянии 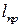 от точки подвеса маятника О, называется центром качания физического маятника. Центр качания
от точки подвеса маятника О, называется центром качания физического маятника. Центр качания 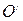 и точка подвеса О обладают свойством взаимности (обратимости): если маятник подвесить так, чтобы его ось качаний проходила через точку
и точка подвеса О обладают свойством взаимности (обратимости): если маятник подвесить так, чтобы его ось качаний проходила через точку 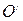 , то точка О будет совпадать с новым положением центра качания маятника, то есть приведённая длина и период колебаний маятника останутся прежними. Этот принцип используется в оборотном маятнике для определения ускорения свободного падения.
, то точка О будет совпадать с новым положением центра качания маятника, то есть приведённая длина и период колебаний маятника останутся прежними. Этот принцип используется в оборотном маятнике для определения ускорения свободного падения.
Покажем, что при закреплении маятника в центре качания 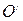 приведённая длина, а значит и период колебаний, будут теми же, что и при закреплении маятника в точке О.
приведённая длина, а значит и период колебаний, будут теми же, что и при закреплении маятника в точке О.
Действительно, по теореме Штейнера:
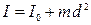 (8)
(8)
где 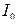 - момент инерции относительно оси, проходящей через центр тяжести маятника.
- момент инерции относительно оси, проходящей через центр тяжести маятника.
Тогда формула (7) примет вид:
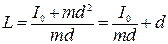 . (9)
. (9)
Для маятника колеблющегося около оси, проходящей через центр качания 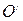 (по аналогии), имеем:
(по аналогии), имеем:
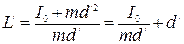 . (10)
. (10)
Из рисунка 1 видно, что 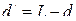 , следовательно
, следовательно
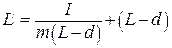 . (10/)
. (10/)
С другой стороны из формулы (9) видно, что 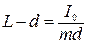 .
.
Подставляя это выражение для 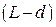 в формулу (10) получим:
в формулу (10) получим:
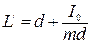 .
.
Сопоставляя с формулой (9) получим, что
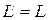 . (11)
. (11)
Таким образом, точка подвеса и центр качания обладают свойствами обратимости: при переносе точки подвеса в центр качания прежняя точка подвеса становится новым центром качания. Отсюда и название физического маятника, который можно обернуть и подвесить за центр качания, - «оборотный маятник».
|
|
|
|
|
|



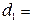 ….(м);
….(м); 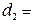 ….(м);
….(м); 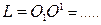 (м);
(м);