 |
Момент инерции тела относительно оси
|
|
|
|
Моментом инерции тела относительно любой оси, например, 
(рис.1), понимают величину равную сумме произведений масс 
отдельных материальных частиц на квадраты их расстояний 
от данной оси:
(1)
Взятое отдельно слагаемое 
(кг·м2), представляет собой момент инерции 
-ой материальной частицы (точки) относительно той же оси.
Рис унок 1 – Момент инерции твёрдого тела относительно оси
Момент инерции тела ( скалярная величина) является мерой инертности тела по отношению к вращательному движению; он аналогичен массе при поступательном движении.
Исходя из определения момента инерции видно, что для данного тела, в принципе, можно вычислить бесчисленное множество моментов инерции, поскольку может быть выбрано бесчисленное множество осей, относительно которых могут быть вычислены моменты инерции. Практически интересуются моментами инерции тела относительно только тех осей, вокруг которых тело совершает или будет совершать вращательное движение. Очень часто, например, необходимо знать момент инерции тела относительно оси его симметрии. Задача отыскания моментов инерции твёрдых тел по формуле (1) при разбиении тела на бесконечно большое число элементарных участков (рис.2) сводится к вычислению интеграла вида:
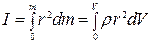, (2)
где 
- плотность вещества, 
- элемент объёма.
Рисунок 2 – Определение момента инерции д ля тела с непрерывным распределением массы
Вычисление моментов инерции по формуле (2) является простой задачей только для тел сравнительно простой формы и относительно осей симметрии, проходящих через центры масс тела.
Моменты инерции других тел правильной формы представлены в таблице.
|
|
|
Таблица – Момент инерции 
некоторых тел, вычисленных относительно оси вращения, проходящей через центр масс
| Твёрдое тело | Ориентация оси | Момент инерции 
|
| Тонкое кольцо, обруч, колесо, полый тонкостенный цилиндр | 
|
|
| Диск, сплошной цилиндр |  
| 
|
| Полый тонкостенный цилиндр | 
| 
|
| Диск | 
|
|
| Шар, полая тонкостенная сфера | 
| 
|
| Тонкий стержень, четырехугольная пластина | 
| 
|
Теорема Штейнера
Параллельное смещение оси вращения, проходящей через центр масс, приводит к увеличению момента инерции данного тела.
Вычисление моментов инерции тела относительно осей, не являющихся осями симметрии, проходящими через центры масс тела, является задачей довольно сложной. Если известен момент инерции относительно оси, проходящей через центр инерции тела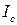 
, то можно вычислить момент инерции относительно параллельной оси.
В этом случае иногда используют теорему Штейнера: момент инерции 
относительно произвольной оси равен сумме его момента инерции 
относительно оси, параллельной данной и проходящей через центр инерции тела, и произведению массы тела на квадрат расстояния d между осями:
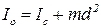(3)
Методика определения момента инерции детали
В данной работе определяются моменты инерции детали определённой формы относительно некоторых осей, не проходящих через центр тяжести этого тела. Так как в этом случае тело представляет собой так называемый физический маятник, то определение момента инерции детали основано на выводах, следующих из теории по колебаниям физического маятника, изложенной ниже.
При отклонении маятника от положения равновесия на угол 
(рис. 3) возникает решающий момент 
, стремящийся возвратить маятник в положение равновесия. Этот момент равен:
,(4)
где 
- масса маятника,
- расстояние между точкой подвеса и центром массы маятника,
- ускорение свободного падения.
|
|
|
Рис унок 3 – Схема определения момента силы
На основании основного закона динамики вращательного движения можно записать:
, (5)
где 
- момент инерции маятника относительно оси 
.
(Знак «-» обусловлен тем, что за положительный момент принимают момент, вращающий тело противчасовой стрелки).
Будем рассматривать только малые колебания, тогда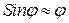 
и выражение (5) принимает вид:
. (6)
Поделив выражение (6) на 
и обозначив 
(7)
получим:
. (8)
Решением дифференциального уравнения (8) является выражение:
, (9)
где 
- амплитуда колебаний,
- циклическая частота колебаний,
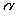- начальная фаза.
В том, что выражение (9) действительно является решением уравнения (8) легко убедиться, подставив (9) в (8). Из (9) следует, что при малых отклонениях от положения равновесия и отсутствии трения физический маятник совершает гармонические колебания.
Период колебаний 
маятника связан с соотношением:
. (10)
Из соотношений (7) и (10) следует, что период колебаний физического маятника равен:
. (11)
Обозначим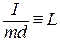 
. (12)
Тогда 
. Это выражение по виду совпадает с формулой периода колебаний математического маятника:
,
где 
- длина математического маятника.
В связи с этим 
называют приведённой длиной физического маятника. Таким образом, приведённая длина 
физического маятника – это длина такого математического маятника, период колебаний которого равен периоду колебаний данного физического маятника.
Точка 
(рис. 3) на прямой, соединяющей точку подвеса с центром масс, лежащая на расстоянии приведенной длины от оси вращения, называется центром качания физического маятника.
Можно показать, что при закреплении маятника в центре качания (в точке ), приведённая длина, а, следовательно, и период колебаний, будет тем же, что и при закреплении маятника в точке подвеса .
Из формулы (11) следует, что момент инерции физического маятника может быть определён по формуле:
, (13)
а из формулы (12) видно, что он может быть определен и как:
. (14)
ОПИСАНИЕ УСТАНОВКИ
Установка представляет собой вертикальную стойку (рис.4а), укреплённую на основании 2. Для подвеса детали 3, в верхней части стойки закреплена призма 4. На конце призмы закреплён зажим 5 для подвеса и изменения длины математического маятника 6, который используется здесь в качестве отвеса.
|
|
|
В данной работе момент инерции детали 3 определяется относительно двух осей 
и 
(рис. 4б). На этой детали отмечены центр качаний и центр масс 
( - это центр качания при колебаниях около оси 
).
А б
Рис унок 4 (а, б) – Схема установки для определения момента инерции детали
|
|
|
