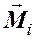 |
Вращение тела вокруг неподвижной оси
|
|
|
|
Вращение твердого тела вокруг неподвижной оси очень распространено в технике. Именно такое движение совершают, например, различные маховики, которые обеспечивают более равномерное вращение тела, «сглаживают» возможные рывки за счет своей инерционности. В быту маховики Вы могли видеть в бабушкиной швейной машине с ножным приводом. Отличительная особенность конфигурации маховиков заключается в том, что конструкторы стремятся расположить основную массу маховика возможно дальше от оси вращения. Это связано с тем, что инерция тела при вращении определяется не только его массой, но и ее пространственным распределением.
Поэтому рассмотрим подробно практически наиболее интересный случай, когда абсолютно твердое тело вращается с угловой скоростью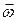 
вокруг неподвижной оси Z (рисунок 4.1).
Для любой системы частиц, и для твердого тела, как системы жестко связанных частиц с массами 
и радиус-векторами 
, справедливо уравнение:
. (4.6)
где 
– момент внешних сил, действующих на i -тое тело системы.
|
|
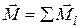. Представим, что тело вращается с угловой скоростью 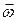, направленной вдоль оси вращения.
Положение 
-той частицы тела с массой 
зададим радиус-вектором 
, проведенным из начала отсчета – точки О, лежащей на оси вращения. За счет участия во вращении тела движется с линейной скоростью 
и обладает моментом пульса относительно точки О:
, (4.7)
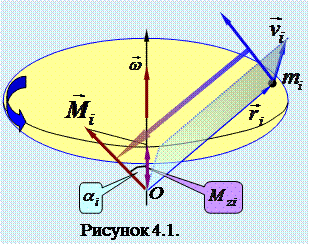
и на рисунке показан синей стрелкой. В соответствии с определением момента пульса, он направлен перпендикулярно плоскости, построенной на векторах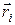 
и . Если вектор момента импульса отложить от начала отсчета (коричневая стрелка), то видно, что он образует с осью Z угол 
, а его проекция на ось вращения равна 
.
|
|
|
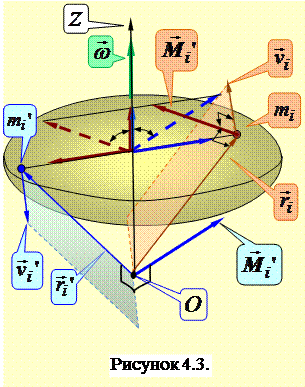
В общем случае, для тела произвольной формы, несимметричного относительно оси Z, момент импульса тела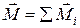 
не совпадает по направлению с осью вращения Z, и при вращении тела поворачивается вместе с ним вокруг этой оси, описывая вокруг нее конус. Например, для отдельной материальной точки (рисунок 4.2) при ее вращении вокруг оси Z момент импульса лежит в плоскости, образованной осью Z и радиус-вектором 
. При повороте точки меняется ориентация в пространстве этой плоскости и вектора момента импульса 
. Поведение вектора можно представить, если откладывать его от точки О, из которой проведен радиус-вектор к рассматриваемой материальной точке. Очевидно, что конец вектора движется по окружности, а сам вектор описывает конус.
Однако, к счастью, вращение несимметричных тел встречается на практике весьма редко.
Если тело является однородным и симметричным относительно Z, то 
совпадает по направлению с Z и 
. Действительно, в симметричном теле для каждой 
найдется симметрично расположенная в теле точка 
. Ее момент импульса 
, равный по модулю , будет расположен относительно оси под таким же углом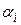 
. Составляющие этих векторов вдоль оси вращения одинаково направлены и складываются. Составляющие, перпенди-кулярные оси Z, направлены встречно и в суммарном моменте импульса тела уничтожают друг друга. Поэтому у симметричного и однородного тела момент импульса направлен по оси вращения, вдоль вектора угловой скорости. При этом модуль момента импульса тела складывается из проекций на ось вращения моментов импульса 
частиц тела. Поэтому этой проекции - - уделим особое внимание.
Тангенциальная скорость точки всегда перпендикулярна плоскости, проведенной через точку и ось вращения. Поскольку радиус-вектор точки 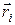лежит в этой плоскости, то радиус-вектор перпендикулярен ее скорости, т.е. 
, и угол 
равен 
. Поэтому выражение для модуля момента импульса -той частицы (в соответствии с (4.7) 
) запишем в виде:
|
|
|
(4.8)
(учтено то, что синус в векторном произведении равен единице в силу того, что ).
Обозначим расстояние от данной точки тела до оси вращения 
и учтем, что линейная скорость точки 
. Тогда для модуля момента импульса получим 
.
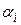Для любой угол между векторами 
и 
является острым (если Вы не уверены, то постройте вектор 
для нескольких точек). Поэтому проекции векторов и 
на ось Z имеют одинаковые знаки, и можно записать:
. (4.9)
При этом мы воспользовались тем, что угол между перпендикуляром (
), опущенным из на ось вращения, и радиус вектором 
равен , поскольку эти углы имеют взаимно перпендикулярные стороны.
Просуммировав (4.9) по всем , получим, что
. (4.10)
Из этого соотношения следует, что проекция момента импульса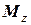 
не зависит от того, относительно какой точки О на оси вращения берется момент импульса . Действительно – ведь в выражение (4.10) входят не радиус-векторы масс , а только их расстояния 
до оси вращения Z.
По определению моментом инерции тела относительно оси называется величина:
. (4.11)
Тогда соотношение (4.10) можно записать в виде:
. (4.12)
Очевидно, что по форме соотношение (4.12) очень напоминает определение импульса материальной точки: 
. Соответственно момент инерции является именно той величиной, которая определяет инерционные свойства тела во вращательном движении, и зависит он, как и следовало ожидать, не только от массы тела, но и от распределения массы в пространстве, от формы тела (совокупность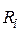 
). Причем для материальной точки зависимость ее момента инерции от расстояния до оси вращения является квадратичной!
В соответствии с (4.6) (взяв проекцию уравнения на ось Z):
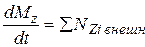(4.13)
В частном (!!!) случае, если расположение частиц тела не изменяется, его момент инерции не изменяется (
), и
, (4.14)
где 
есть угловое ускорение тела.
Таким образом, для твердого тела справедливо соотношение:
. (4.15)
(Сравните формулу (4.13) со вторым законом Ньютона в виде 
, а (4.15) с формулой для с постоянной массой: 
)
Если тело является однородным и симметричным относительно оси Z, то вектор момента импульса тела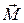 
совпадает по направлению с Z и , и можно записать в векторном виде:
|
|
|
, 
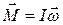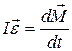(4.16)
Следует иметь в виду, что соотношение (4.15) справедливо для любого тела, а (4.16) только для симметричного тела. Однако именно это соотношение на практике используется чаще всего. (4.16) часто называют основным уравнением динамики вращательного движения.
Можно доказать, что для произвольного тела существуют три взаимно перпендикулярные оси вращения, проходящие через его центр масс, такие, что при вращении тела вокруг них и отсутствии внешних сил их положение в пространстве сохраняется. Эти оси называют главными осями инерции. При вращении тела относительно главных осей инерции справедливо соотношение (4.16).
МОМЕНТ ИНЕРЦИИ
Момент инерции, аналогично массе тела, в соответствии с его определением (4.11) является величиной аддитивной и может считаться характеристикой тела, независимо от того, вращается оно или нет.
В значительной степени момент инерции зависит от распределения массы в пределах тела, которое характеризуют плотностью тела:
(4.17)
Под 
в (4.17) понимается физически бесконечно малый объем, т.е. настолько малый, что все макроскопические свойства в его пределах можно считать постоянным, но достаточно большой, чтобы не проявлялась дискретностью строения вещества.
Соответственно, точная формула для вычисления 
получается из (4.11) и имеет вид:
. (4.18)
По сравнению с (4.11) в (4.18) заменены на бесконечно малые 
, находящиеся от оси вращения на расстоянии 
.
В качестве примера использования формулы (4.18) рассмотрим вычисление момента инерции однородного диска радиуса 
относительно оси, перпендикулярной к его плоскости и проходящей через его центр. Разобьем мысленно диск (рисунок 4.5.) на кольцевые слои с радиусом и толщиной 
, толщина диска равна b. Объем кольцевого слоя
(4.19)
Его масса 
. Все точки кольцевого слоя находятся на одинаковом расстоянии от оси вращения, поэтому его момент инерции
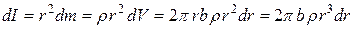. (4.20)
Момент инерции всего диска равен сумме моментов инерции кольцевых слоев:
|
|
|
. (4.21)
 |
Аналогично можно рассчитать моменты других тел с правильной геометрической формой. Для шара:
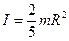, для тонкого однородного стержня длинной 
:
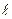, для тонкого диска, относительно оси, лежащей в его плоскости и проходящей через центр: 
.
 |
Вычисление моментов инерции для тел сложной формы значительно облегчается при использовании теоремы Штейнера: момент инерции тела относительно произвольной оси равен сумме момента инерции
относительно оси, параллельной данной и проходящей через центр масс тела, и произведения массы тела на квадрат расстояния между осями d: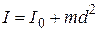 
.
Например, при вращении сложного тела, по форме напоминающего гантель (рисунок 4.7) вокруг оси «ОО» проходящей через центр одного из шаров, его момент инерции можно представить состоящим из трех составляющих: момента инерции левого шара, стержня и правого шара. Последние в свою очередь по теореме Штейнера состоят из двух частей – момента инерции относительно оси проходящей через центр масс и произведения массы соответствующего тела на квадрат расстояния между осями.
|
|
|
