 |
23. Множественные сравнения. Непосредственная оценка
|
|
|
|
23. Множественные сравнения. Непосредственная оценка
Множественные сравнения отличаются от парных сравнений тем, что экспертам последовательно предъявляются не пары, а тройки, четверки, …, n-ки (n< N) объектов. Эксперт их упорядочивает по важности или разбивает на классы в зависимости от целей экспертизы.
Множественные сравнения занимают промежуточное положение между парными сравнениями и ранжированием. С одной стороны, они позволяют использовать больший, чем при парных сравнениях, объем информации для определения экспертного суждения в результате одновременного соотнесения объекта не с одним, а с большим числом объектов. С другой стороны, при ранжировании объектов их может оказаться слишком много, что затрудняет работу эксперта и сказывается на качестве результатов экспертизы. В этом случае множественные сравнения позволяют уменьшить до разумных пределов объем поступающей к эксперту информации.
Непосредственная оценка.
Метод непосредственной оценки заключается в присваивании объектам числовых значений на шкале интервалов. Эксперту необходимо поставить в соответствие каждому объекту точку на определенном отрезке числовой оси. При этом необходимо, чтобы эквивалентным объектам приписывались одинаковые числа.
Тип шкал интервалов содержит шкалы, единственные с точностью до множества положительных линейных допустимых преобразований. Измерения на шкале интервалов могут быть достаточно точными при полной информированности экспертов о свойствах объектов. Эти условия на практике встречаются редко, поэтому для измерения применяют бальную оценку. При этом вместо непрерывного отрезка числовой оси рассматриваются участки, которым приписываются баллы.
|
|
|
Эксперт приписывает объекту балл, тем самым измеряет его с точностью до отрезка числовой оси. Применяются 5-ти, 10-ти и 100 бальные шкалы.
24. Последовательное сравнение (метод Черчмена Акоффа).
Этот метод относится к числу наиболее популярных при оценке альтернатив. В нем предполагается последовательная корректировка оценок, указанных экспертами. Основные предположения, на которых основан метод, состоят в следующем:
- каждой альтернативе ai, (i=1,..., n) ставится в соответствие действительное неотрицательное число ϕ (ai);
- если альтернатива ai≻ aj, то ϕ (ai)> ϕ (aj), если же ai≈ aj, то ϕ (ai)=ϕ (aj);
- если ϕ (ai) и ϕ (aj) – оценки альтернатив ai и aj, то сумма ϕ (ai)+ϕ (aj) соответствует совместному осуществлению альтернатив ai и aj
Наиболее сильным является последнее предположение об аддитивности оценок альтернатив.
Согласно методу Черчмена-Акоффа альтернативы ранжируются по предпочтительности. Пусть альтернатива a1 наиболее предпочтительна, за ней следует a2 и т. д. Эксперт указывает предварительные численные оценки ϕ (ai) для каждой из альтернатив. Иногда наиболее предпочтительной альтернативе приписывается оценка 1, остальные оценки располагаются между 0 и 1 в соответствии с их предпочтительностью. Затем эксперт производит сравнение альтернативы a1, и суммы альтернатив a2,..., aN. Если a1 предпочтительнее, то эксперт корректирует оценки так, чтобы
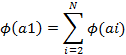
После того как альтернатива a1 оказывается предпочтительней суммы альтернатив a2,..., ak(k> 2), она исключается из рассмотрения, а вместо оценки альтернативы a1 рассматривается и корректируется оценка альтернативы a2. Процесс продолжается до тех пор, пока откорректированными не окажутся оценки всех альтернатив.
При достаточно большом N применение метода Черчмена-Акоффа становится трудоемким. В этом случае целесообразно разбить альтернативы на группы, а одну из альтернатив, например максимальную, включить во все группы. Это позволяет получить численные оценки всех альтернатив с помощью оценивания внутри каждой группы. Данный метод считается одним из самых эффективных.
|
|
|
25. Методы Неймана-Моргенштерна и согласования оценок.
Метод Неймана-Моргенштерна заключается в получении численных оценок альтернатив с помощью, так называемых, вероятностных смесей. В основе метода лежит предположение, согласно которому эксперт для любой альтернативы aj менее предпочтительной, чем ai, но более предпочтительной чем a1(a1≺ aj≺ ai) может указать число ap(0≤ p≤ 1) такое, что альтернатива aj эквивалентна смешанной альтернативе (вероятностной смеси) [pai(1− p)a1]. Смешанная альтернатива состоит в том, что альтернатива ai, выбирается с вероятностью p, а альтернатива a1 - с вероятностью 1− p. Очевидно, что если p достаточно близко к 1, то альтернатива aj менее предпочтительна, чем смешанная альтернатива [pai, (1− p)a1].
Если указанная система предпочтений выполнена, то для каждой из набора основных альтернатив a1, a2,..., aN определяются числа x1, x2,..., xN характеризующие численную оценку смешанных альтернатив. Численная оценка смешанной альтернативы [p1a1, p2a2,..., pNaN] равна:
p1x1=p2x2+... +pNxN
Таким образом, устанавливается существование функции полезности, значение которой характеризует степень предпочтительности любой смешанной альтернативы. Более предпочтительна та смешанная альтернатива, для которой значение функции полезности больше.
Метод согласования оценок
Этот метод обычно применяется при обработке индивидуальных экспертных оценок. Метод имеет много вариантов, различающихся способами, при помощи которых из индивидуальных оценок получается обобщенная. При этом используют различные методы согласования оценок:
1) Простейшие, основанные на получении средней вероятности,
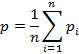
или средневзвешенного значения вероятности

Где ki – веса, приписываемые оценке каждого эксперта;
2) Специальные методы оценки измерения и повышения коэффициентов согласованности (или коэффициентов непротиворечивости) мнений экспертов;
3) Методы, основанные на отборе экспертной группы с высоким коэффициентом согласованности мнений.
|
|
|
Наиболее часто при обработке материалов коллективной экспертной оценки используются методы теории ранговой корреляции. Для количественной оценки степени согласованности мнений экспертов применяется коэффициент конкордации W, который позволяет оценить, насколько согласованы между собой ряды предпочтительности, построенные каждым экспертом. Его значение находится в пределах.
– полную противоположность, полное совпадение ранжировок. Практически достоверность считается хорошей, если. Небольшое значение коэффициента конкордации, свидетельствующее о слабой согласованности мнений экспертов, является следствием следующих причин:
в рассматриваемой совокупности экспертов действительно отсутствует общность мнений;
внутри рассматриваемой совокупности экспертов существуют группы с высокой согласованностью мнений, однако обобщенные мнения таких групп противоположны.
Для наглядности представления о степени согласованности мнений двух любых экспертов A и B служит коэффициент парной ранговой корреляции p, он принимает значения от -1 до +1. Значение соответствует полному совпадению оценок в рангах двух экспертов (полная согласованность мнений двух экспертов), а p=− 1 – двум взаимно противоположным ранжировкам важности свойств (мнение одного эксперта противоположно мнение другого).
Рассмотренные выше методы экспертных оценок обладают различными качествами, но приводят в общем случае к близким результатам. Практика применения этих методов показала, что наиболее эффективно комплексное применение различных методов для решения одной и той же задачи. Сравнительный анализ результатов повышает обоснованность выводов. При этом следует учитывать, что методом, требующим минимальных затрат, является ранжирование, а наиболее трудоемким – метод последовательного сравнения (Черчмена-Акоффа). Метод парного сравнения без дополнительной обработки не дает полного упорядочения объектов.
|
|
|


