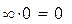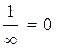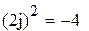|
3. Точность представления результатов вычислений.
|
|
|
|
3. Точность представления результатов вычислений.
Обратимся к вкладке Tolerance. В этом разделе вы увидите два поля:
“Сomplex threshold” – порог комплексных чисел. Имеется в виду число m, которое определяет по соотношению действительной и мнимой частей, когда следует принять равной нулю при отображении на экране действительную или мнимую часть полученного численным процессором комплексного числа A=a+b·i. Число m может принимать значения от 0 до 63 (по умолчанию – 10). Это означает, что:
если  , то а полагаем равным нулю
, то а полагаем равным нулю
если  , то b полагаем равным нулю
, то b полагаем равным нулю
“Zero threshold” – порог нуля. В этом поле задается число k от 0 до 307 (по умолчанию – 15). Результаты, чья абсолютная величина меньше, чем 10-k на экране представляются как 0 (при этом внутреннее представление результата не меняется).
Замечание. Эта опция доступна только в том случае, если не выделен конкретный результат. То есть, прежде чем вызвать диалоговое окно “Result Format”, щелкните мышью на пустом месте документа.
Порог нуля на много порядков меньше, чем машинный нуль. Эта опция введена для того, чтобы уменьшить стресс пользователя от неизбежной погрешности вычислений. Пользователь хорошо знает, что
sin(π ) = 0
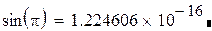 |
Но если увеличить значение k, к примеру, k=17, то он увидит на экране вместо ожидаемого нуля:
(если в поле Number of decimal places формата General стоит число 6). Вы можете выбрать другой формат и увеличить Number of decimal places, но точность вычислений от этого не изменится и ожидаемого нуля вы не увидите.
Отметим, что, предлагаемые по умолчанию пороговые значения в версии Mathcad 12 не изменились.
В заключение еще раз подчеркнем, что Zero threshold не влияет на точность вычислений, которая для численного процессора определяется длиной мантиссы.
|
|
|
4. Особенности работы численного процессора Mathcad с числом «0» и символом «∞ ».
Язык общения Mathcad использует общепринятый в математике символ бесконечности «∞ ». Но численный и символьный процессоры Mathcad воспринимают этот символ по-разному. Численный процессор понимает под символом «∞ » конкретное число:

что, разумеется, противоречит общепринятому в математике значению символа «∞ ». Поэтому, работая с численным процессором, мы получим равенства:
|
|
|
|
|
|
|
|
|
|
|
|
Отметим, что символьный процессор воспринимает символ «∞ » абсолютно правильно и наотрез отказывается производить с ним арифметические действия (формула становится красной и появляется сообщение об ошибке).
 |
Особенное удивление, несомненно, вызовет следующий результат вычислений численного процессора:
По-видимому, численный процессор, обнаружив нуль в числителе, принимает дробь равной нулю, что верно для любого знаменателя, кроме нулевого. Почему разработчики численного процессора не включили проверку знаменателя на равенство нулю даже в 12-той версии неизвестно. Символьный процессор, созданный другим коллективом, разумеется, нуль на нуль не делит.
5. Вычисления с комплексными числами.
5. 1. Представление комплексных чисел.
Для обозначения мнимой единицы Mathcad использует две буквы - i и j. Чтобы использовать букву j, обратитесь к вкладке Display Options окна “Result Format” и выберите в окошке “Imaginary value” вариант «j (J)». Отметим, что изменение буквы i на j относится только к выводу информации. Например, равенства:
|
|
|
|
|
|
 |
будут выполнены вне зависимости от того, какая буква установлена в опции “Imaginary value”. Если установлена буква i, то:
а если буква i заменена на j, то:
|
|
Для того, чтобы Mathcad воспринимал буквы i или j как мнимую единицу, они должны быть введены непосредственно вслед за цифрой (без знака умножения). Кроме того, мнимую единицу можно выбрать из палитры “ Calculator ”.
|
|
|
Отметим, что символьный процессор также воспринимает буквы i или j, введенные непосредственно после цифр как мнимую единицу, но при выводе результатов использует для обозначения мнимой единицы только букву i. Например:

5. 2. Важнейшие встроенные функции и операторы Mathcad
для работы с комплексными числами.
Важнейшие встроенные функции для работы с комплексными числами перечислены в таблице 1 (см гл. 1 п. 2 ). Добавим к ним еще одну функцию:
Пусть z = a + b× i. Функция angle (a, b) вычисляет угол между осью абсцисс и вектором z. В отличие от функции arg (z) (см. таблицу 1), результат которой удовлетворяет ограничениям:

результат вычисления функции angle (a, b) лежит в пределах:

Например,
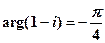

5. 2. 1. Преобразование алгебраической и показательной формы
комплексного числа.
В системе Mathcad численный процессор преобразует комплексное число, записанное в показательной форме в алгебраическую форму посредством оператора «=», а символьный процессор - посредством оператора «®»:
 , где
, где 
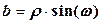
 w записано в радианах
w записано в радианах
Численный и символьный процессоры производят все арифметические действия с числами, записанными как в алгебраической, так и в показательной форме, но результат вычислений всегда представляет собой комплексное число в алгебраической форме.
В Mathcad нет оператора, непосредственно преобразующего в алгебраическую форму представления комплексного числа в показательную.
|
|
|