 |
4. Действия с векторами и матрицами.
|
|
|
|
4. Действия с векторами и матрицами.
4. 1. Векторные и матричные операторы.
Mathcad может выполнять с векторами и матрицами большое количество различных операций. Причем к таким стандартным операциям как умножение и деление на скаляр, в Mathcad добавлены операции, позволяющие вычесть или прибавить скаляр к каждому элементу вектора или матрицы. В таблице 2 вы найдете перечень векторных и матричных операторов.
Замечание 1. Здесь и далее приняты следующие обозначения:
М – матрица, v - вектор, z –скаляр, n – целое число.
Замечание 2. Предметом рассмотрения данной главы являются числовые векторы и матрицы и действия с ними. Mathcad может использовать в преобразованиях и символьные матрицы.
Таблица 2. Векторные и матричные операторы.
| Операция | Изображение | Используемые клавиши | Описание |
| Умножение вектора на скаляр | z× v v× z | z*v v*z | Каждый элемент вектора v умножается на число z |
| Умножение матрицы на скаляр | z× M M× z | z*M M*z | Каждый элемент матрицы M умножается на число z |
| Деление вектора на скаляр | 
| v/z | Каждый элемент вектора v делится на число z |
| Деление матрицы на скаляр | 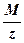
| M/z | Каждый элемент матрицы M делится на число z |
| Прибавление скаляра к вектору | z+v v+z | z+v v+z | К каждому элементу вектора v прибавляется число z |
| Прибавление скаляра к матрице | z+M M+z | z+M M+z | К каждому элементу матрицы M прибавляется число z |
| Вычитание скаляра из вектора | z-v v-z | z-v v-z | Из каждого элемента вектора v вычитается число z |
| Вычитание скаляра из матрицы | z-M M-z | z-M M-z | Из каждого элемента матрицы M вычитается число z |
| Операция | Изображение | Используемые клавиши | Описание |
| Сложение двух векторов | v1+v2 | v1+v2 | Векторы v1 и v2 должны иметь одинаковую размерность |
| Сложение двух матриц | M1+M2 | M1+M2 | Матрицы M1 и M2 должны иметь одинаковую размерность |
| Вычитание двух векторов | v1-v2 | v1-v2 | Векторы v1 и v2 должны иметь одинаковую размерность |
| Вычитание двух матриц | M1-M2 | M1-M2 | Матрицы M1 и M2 должны иметь одинаковую размерность |
| Смена знака вектора | -v | -v | Ответ – вектор той же размерности, с элементами противоположного знака |
| Смена знака матрицы | -M | -M | Ответ – матрица той же размерности, с элементами ротиивоположного знака |
| Точечное (скалярное) произведение | v1× v2 | v1*v2 | Векторы v1 и v2 должны иметь одинаковую размерность. Результат – число: 
|
| Векторное произведение | v1´ v2 | v1 [Ctrl]* v2 | Векторы v1 и v2 должны быть трехэлементными |
| Произведение двух матриц | M1× M2 | M1*M2 | Число строк матрицы М1 должно быть равно числу столбцов матрицы М2 |
| Умножение матрицы на вектор | M× v | M*v | Число строк матрицы М должно быть равно длине вектора v |
| Обращение матрицы | М-1 | М-1 | Матрица М должна быть квадратной |
| Возведение матрицы в степень | М n | М n | Матрица М должна быть квадратной |
| Модуль вектора | |v| | | v | Результат – число: 
|
| Определитель матрицы | |М| | | М | Матрица М должна быть квадратной |
| Транспонирование вектора | vT | v [Ctrl]! | Если v – вектор-столбец, результат – вектор-строка и наоборот |
| Транспонирование матрицы | МT | М [Ctrl]! | Если М – матрица размерности mxn, результат – матрица размерности nxm |
|
|
|
| Операция | Изображение | Используемые клавиши | Описание |
| Вычисление суммы элементов вектора | Sv | [Alt] $ v | Результат – число: 
|
| Векторизация вектора | 
| v [Ctrl] - | См. п. 4. 4. |
| Векторизация матрицы | 
| М [Ctrl] - | См. п. 4. 4. |
| Верхний индекс | Мá nñ | М [Ctrl] n | Результат – n-ный столбец матрицы |
| Нижний индекс вектора | vn | v [ n | Результат – n-ный элемент вектора |
| Нижний индекс матрицы | Мn, m | M [ (n, m) | Результат –элемент матрицы М с координатами (n, m) |
| Комплексное сопряженное |  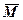
| v» М» | Результат –комплексное сопряженное вектора v или матрицы М |
Все перечисленные в этой таблице операторы (кроме последнего) можно также вызвать из палитры “ Vector and Matrix ”.
|
|
|
4. 2. Векторные функции.
Mathcad также содержит ряд встроенных функций, аргументом которых может быть вектор. В таблице 3 вы найдете список таких функций.
Таблица 3. Векторные функции.
| Функции | Описание |
| length(v) | Число элементов вектора v |
| last(v) | Номер последнего элемента вектора v |
| max(v) | Максимальный элемент вектора v |
| min(v) | Минимальный элемент вектора v |
| Re(v) | Действительная часть чисел-элементов вектора v |
| Im(v) | Мнимая часть чисел-элементов вектора v |
| mean(M) | Среднее значение элементов вектора v |
| median(M) | Медиана элементов вектора v |
4. 3. Матричные функции.
Mathcad содержит большое количество встроенных функций, предназначенных для работы с матрицами. Эти функции можно разделить на несколько групп (см. таблицу 4).
Таблица 4. Матричные функции.
| Функции | Описание | ||
|
Создание матриц специального вида | |||
| identity(n) | Единичная матрица размерности nxn | ||
| diag(v) | Диагональная матрица, по главной диагонали которой расположены элементы вектора v | ||
| geninv(М) | Левая обратная к матрице М матрица L, такая, что L× M=I (где M-вещественнаяматрица размерности mxn, причем m³ n, I – единичная матрица, содержащая n столбцов) | ||
| rref(М) | Ступенчатая форма матрицы М | ||
| matrix(m, n, f) | Матрица размерности mxn, в которой (i, j)-й элемент равен f(i, j), где f(i, j) – некоторая функция | ||
|
Формирование новых матриц из имеющихся | |||
| augment(M1, M2) | Матрица образуется присоединением М2 к М1 справа (аргументами могут быть не только матрицы, но и вектора). М2 и М1 должны иметь одинаковое количество строк | ||
| stack(M1, M2) | Матрица образуется присоединением М2 к М1 снизу (аргументами могут быть не только матрицы, но и вектора). М2 и М1 должны иметь одинаковое количество столбцов | ||
| submatrix(M, ir, jr, ic, jc) | Подматрица, содержащая строки матрицы М с номерами от ir до jr и ее столбцы с номерами от ic до jc | ||
| Re(М) | Действительная часть чисел-элементов матрицы М | ||
| Im(М) | Мнимая часть чисел-элементов матрицы М | ||
|
Специальные характеристики матриц
| |||
| cols(M) | Число столбцов матрицы М | ||
| Функции | Описание | ||
| max(М) | Максимальный элемент матрицы М | ||
| min(М) | Минимальный элемент матрицы М | ||
| rank(M) | Ранг матрицы М | ||
| tr(M) | След (сумма диагональных элементов) матрицы М | ||
| mean(M) | Среднее значение элементов матрицы М | ||
| median(M) | Медиана элементов матрицы М | ||
| cond1(M) | Число обусловленности матрицы M, вычисленное в норме L1 | ||
| cond2(M) | Число обусловленности матрицы M, вычисленное в норме L2 | ||
| conde(M) | Число обусловленности матрицы M, вычисленное в норме евклидового пространства | ||
| condi(M) | Число обусловленности матрицы M, основанное на равномерной норме | ||
| norm1(M) | Норма L1 матрицы M | ||
| norm2(M) | Норма L2 матрицы M | ||
| norme(M) | Евклидова норма матрицы M | ||
| normi(M) | Неопределенная норма матрицы M | ||
|
Собственные числа и собственные векторы | |||
| eigenvals(M) | Вектор, содержащий все собственные значения матрицы M | ||
| eigenvec(M, z) | Собственный вектор матрицы M, соответствующий ее собственному значению z | ||
| eigenvecs(M) | Матрица, содержащая все собственные векторы матрицы M | ||
Рассмотрим применение некоторых из описанных выше операторов и функций к уже существующим и вновь созданным векторам и матрицам.
|
|
|


