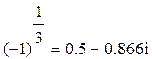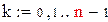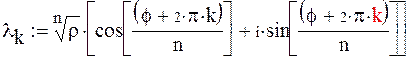 |
6. Вычисление корней и значений степенной функции.
|
|
|
|
6. Вычисление корней и значений степенной функции.
Пусть n и m – целые положительные числа, а w – комплексное число, причем w ¹ 0. В частности, число w может быть действительным и находиться на действительной оси комплексной плоскости. В случае, когда w – действительное число:
arg( w ) = 0, если w > 0
arg( w ) = p, если w < 0
Уравнение:
zn + w = 0
имеет n корней z1 , z2 , …, zn . Далее будут указаны способы вычисления в Mathcad всех n корней. Сначала мы остановимся на вопросе, что вычисляют в Mathcad выражения:
и 
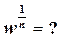
Пусть w – действительное положительное число. В этом случае оба выражения вычисляют действительный положительный корень:
, где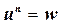 
Если w – отрицательное действительное число и n нечётно, то:
, 
, где 
, 
|
|
|
|
где s – отрицательное действительное число и q¹ s. Иными словами, q и s являются различными числами из множества n корней. Например,
Уравнение z3 + 1 = 0 имеет корни:
Подчеркнем исключительно важное обстоятельство. Численный процессор Mathcad полагает, что
для действительных отрицательных значений w и только для них. Для всех остальных значений w оба выражения равны. Поэтому графики функци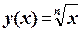й
и 
( n нечётно)
будут совпадать только для положительных значений х.
Для отрицательных значений х график h(x) не существует, так как функция h(x) принимает комплексные значения.
По-видимому, разработчики численного процессора отступили от общепринятого в математике равенства двух выражений для корня n -ной степени для того, чтобы дать возможность пользователю строить графики знакомых со школьных лет функций. Заметим, что символьный процессор не делает указанного различия и трактует обе формы записи одинаково для всех значений w:
|
|
|
В общем случае численный и символьный процессоры принимают значение 
равным тому из n корней уравнения zn + w = 0 , который имеет наименьшее по модулю значение аргумента. Если наименьшее значение модуля аргумента имеют два различных корня, то выбирается тот корень, у которого аргумент положителен.
В рассмотренном примере:
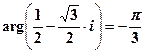
поэтому Mathcad выбирает корень 
.
Рассмотрим, как вычислить все n значений корня.
Если записать комплексное число w в тригонометрической форме:
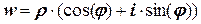
то все значения корней вычисляются по соотношениям:
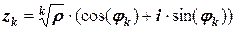где 
, k=0, 1, …, n-1,
которые следуют из формулы Муавра возведения комплексного числа в степень n (n – целое положительное число):
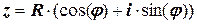
Для того, чтобы вычислить в Mathcad корни по приведённому соотношению, надо использовать ранговую переменную. Пусть дано комплексное число z и величина n.
|
|
|
|
|
|
|
|
Другой способ вычисления всех значений корней – использование встроенной функции polyroots, которая вычисляет все n корней многочлена n -ной степени с комплексными коэффициентами. Подробно работа с функцией polyroots описана в главе 5. Отметим, что разработчики Mathcad в руководстве пользователя и в справочной системе программы используют своеобразную терминологию. Термин “оператор” явно не соответствует математическому термину “оператор”, а процедуры, например процедуру вычисления корней полинома они называют функциями. Поэтому команда, организующая процесс вычисления корней многочлена численным методом называется в Mathcad функцией (так же, как sin или cos).
В заключение рассмотрим вопрос вычисления значений произвольной степенной функции
где z и w – комплексные числа. Mathcad вычисляет число v следующим образом. Число z преобразуется в показательную форму, а число w - в алгебраическую:
w = a + i× b
|
|
|
(действительное число)
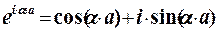(по формуле Эйлера)
Ответ:
, где 
; 
Итоговые упражнения.
1. Вычислите значение выражения:
а) с точностью 3 знака после запятой;
б) с точностью 10 знаков после запятой.
2. Вычислите значение выражения:
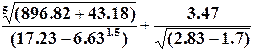
а) в десятичном формате;
б) в инженерном формате;
в) в научном формате;
г) в дробном формате.
3. Вычислите значение выражения:
,
обозначая мнимую единицу
а) буквой i;
б) буквой j.
|
|
|
