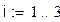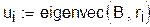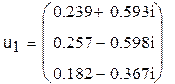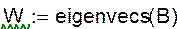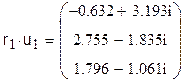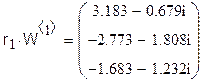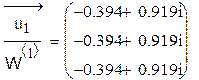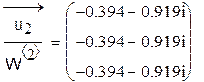|
Пример 1. 1. Поочередно, с помощью функции eigenvec. 2. В одно действие, с помощью функции eigenvecs. B×vi = li× vi (1)
|
|
|
|
Пример 1.
 |
|
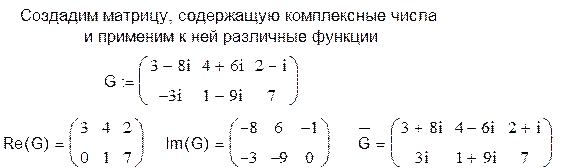 |
Пример 2.
4. 4. Оператор векторизации VEC .
Векторизация – это одновременное применение некоторой скалярной операции ко всем элементам вектора или матрицы. Например, если надо получить матрицу С, каждый элемент которой – произведение соответствующих элементов матриц А и В, т. е.
Сi, j = Ai, j × Bi, j
то проще всего сделать это вы можете именно с помощью оператора VEC:

Для того, чтобы применить к выражению оператор векторизации, обведите все выражение курсором и нажмите [ Ctrl ] – или щелкните по кнопке “Vectorize” из палитры “ Vector and Matrix ”.
 |
Пример 1.
Если М – матрица, то выражение Ö М недопустимо. Применим оператор VEC, чтобы получить матрицу, все элементы которой – квадратные корни из соответствующих элементов матрицы М:
Оператор векторизации обладает следующими свойствами:
1. он изменяет значение операторов и функций, к которым применяется, но не значения имен и чисел;
2. выражение под этим оператором может содержать векторы (все одинаковой длины) или матрицы (все одинаковой размерности) и скаляры. Операции между массивами выполняются поэлементно, а между массивом и скаляром – применением скаляра к каждому элементу массива.
Рассмотрим более сложный пример, где используется не только оператор векторизации, но и другие матричные функции.
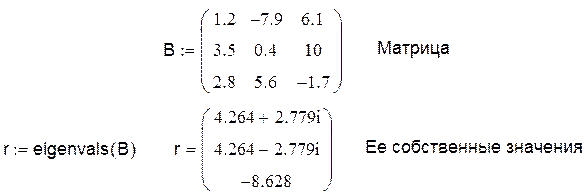 |
Пример 2.
Теперь вычислим все собственные векторы матрицы В двумя способами:
1. Поочередно, с помощью функции eigenvec
|
|
|
|
|
|
|
|
|
|
2. В одно действие, с помощью функции eigenvecs
|
|
|
|
Обескураживает то, что двумя разными способами мы получили для одной и той же матрицы совершенно разные результаты. Проверим, выполняется ли для полученных собственных векторов условие:
|
|
|
B× vi = li× vi (1)
где li – собственное значение матрицы В;
vi – соответствующий ему собственный вектор.
|
|
|
|
|
|
|
|
Как видите, для первого собственного вектора это условие выполняется. Вы можете самостоятельно проверить выполнение условия (1) для двух других собственных векторов.
Разделим поэлементно собственные вектора, полученные двумя разными способами, друг на друга:
|
|
|
|
|
|
Нетрудно заметить, что для каждого собственного вектора имеется один общий множитель. Таким образом, собственные векторы, полученные двумя разными способами, совпадают с точностью до постоянной.
Итоговые упражнения.
1. Создайте произвольную числовую матрицу А размерности 4х4.
2. Определите для матрицы А:
а) значение ее максимального элемента;
б) значение ее минимального элемента;
в) среднее значение ее элементов
3. Удалите из матрицы А первую строку и второй столбец.
4. Извлеките из матрицы А:
а) четвертый столбец;
б) вторую строку.
5. Найдите матрицу, обратную матрице А.
6. Найдите собственные значения матрицы А и ее собственные векторы (двумя способами).
7. Найдите след матрицы А.
8. Создайте два вектора:
v = [2, 4, 7]
w = [3, 1, 2]
и найдите их векторное и скалярное произведения.
9. Вычислите cos каждого элемента матрицы А.
Глава 5. Вычисление корней многочлена.
Многочлены (целые рациональные функции) имеют совершенно исключительное значение в математике, поэтому вопрос о вычислении корней (нулей) многочленов целесообразно рассматривать отдельно.
В Mathcad для вычисления корней многочленов предусмотрены два способа: использование встроенной функции polyroots, работающей с числовым процессором и применение оператора solve, решающего широкий круг задач и работающего с символьным процессором.
|
|
|
|
|
|