 |
Алгебра и геометрия. Конспекты лекций. Векторы. Векторная алгебра. Лекция «векторы. Векторная алгебра». 1. Основные определения
|
|
|
|
АЛГЕБРА И ГЕОМЕТРИЯ
КОНСПЕКТЫ ЛЕКЦИЙ
ВЕКТОРЫ. ВЕКТОРНАЯ АЛГЕБРА
| Содержание | |||
| Название | стр. | Название | стр. |
| 1. Основные определения | 8. 1. Длина вектора | ||
| 2. Действия над векторами | 8. 2. Расстояние между двумя точками | ||
| 2. 1. Умножение вектора на число | 9. Направляющие косинусы вектора | ||
| 2. 2. Сумма векторов | 10. Скалярное произведение двух векторов | ||
| 2. 3. Разность векторов | 10. 1. Определение скалярного произведения | ||
| 3. Числовая ось | 10. 2. Свойства скалярного произведения | ||
| 4. Единичный вектор | 11. Векторное произведение двух векторов | ||
| 5. Угол между векторами | 11. 1. Определение векторного произведения | ||
| 6. Проекция вектора на ось | 11. 2. Свойства векторного произведения | ||
| 7. Системы координат | 12. Смешанное произведение трёх векторов | ||
| 7. 1. Декартова система координат на плоскости | 12. 1. Определение смешанного произведения | ||
| 7. 2. Декартова система координат в пространстве | 12. 2. Свойства смешанного произведения | ||
| 8. Длина вектора. Расстояние между двумя точками | |||
Лекция «Векторы. Векторная алгебра»
Основные определения. Действия над векторами: умножение вектора на число; сумма векторов; разность векторов. Числовая ось. Единичный вектор. Угол между векторами. Проекция вектора на ось. Системы координат: декартова система координат на плоскости; декартова система координат в пространстве. Длина вектора. Расстояние между двумя точками. Направляющие косинусы вектора. Скалярное произведение двух векторов: определение скалярного произведения; свойства скалярного произведения. Векторное произведение двух векторов: определение векторного произведения; свойства векторного произведения. Смешанное произведение трёх векторов: определение смешанного произведения; свойства смешанного произведения
|
|
|
 |
1. Основные определения
В физике и технических науках встречаются величины, которые полностью определяются заданием их численных значений. Эти численные значения являются вещественными числами. Такие величины называются скалярными. Скалярными величинами являются длина, площадь, объём, масса, температура и др.
Наряду со скалярными, встречаются величины, для определения которых необходимо знать их направления в пространстве, например, сила, скорость, ускорение и т. д. Такие величины называются векторными. Они описываются с помощью векторов.
Определение 1. Вектором (свободным вектором) 
называется множество всех направленных отрезков, имеющих одинаковую длину и направление.
О всяком отрезке из этого множества говорят, что он представляет вектор. Одна из ограничивающих его точек принимается за начало, другая – за конец, который на рисунке показывается стрелкой. Если началом вектора является точка 
, а конец точка 
, то используется обозначение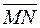 
(рис. 1, рис. 2).
Рис. 1 Рис. 2
Определение 2. Модулем вектора называется его длина. Модуль вектора обозначается 
(аналогично,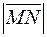 
).
Определение 3. Вектор, у которого конец совпадает с началом, называется нулевым. Нулевой вектор обозначается 
.
Очевидно, что длина нулевого вектора равна нулю: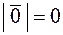 
. У нулевого вектора направление не определено. В качестве направления нулевого вектора можно брать желаемое в данный момент направление.
Определение 4. Векторы и 
называются коллинеарными, если они расположены на параллельных прямых. Коллинеарные векторы называются сонаправленными, если они направлены в одну сторону, и противонаправленными, если они направлены в разные стороны.
|
|
|
На рис. 3 приведены примеры сонаправленных векторов и , и противонаправленных векторов и 
.
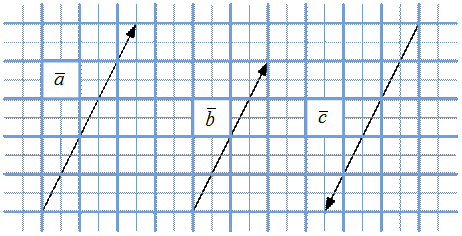
Рис. 3
Определение 5. Векторы и называются равными, если они сонаправлены и имеют одинаковую длину. Равенство векторов и обозначается 
.
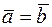Если векторы и равны, то при соединение начало вектора с началом вектора , а конец с концом получится параллелограмм (рис. 4). Верно и обратное правило: если при соединении начало вектора с началом вектора , а конца с концом получится параллелограмм, то векторы и равны.
Если векторы обозначены своими концами 
и 
, то равенство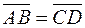 
эквивалентно тому, что четырёхугольник 
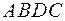является параллелограммом (рис. 5).
Рис. 4 Рис. 5
Определение 5. Вектор называется противоположным вектору , если они противонаправлены и имеют одинаковую длину. Если вектор противоположный вектору , то обозначается 
.
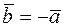Если вектор обозначен с помощью его концов 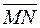, то для обозначения противоположного вектора можно использовать любое из двух обозначений 
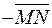или 
.
|
|
|
