 |
10. Скалярное произведение двух векторов
|
|
|
|
10. Скалярное произведение двух векторов
10. 1. Определение скалярного произведения
Определение 19. Скалярным произведением векторов 
и 
называется число, равное произведению их длин на косинус угла между ними и обозначается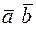 
:
.
Если известны скалярное произведение векторов , и их длины 
, 
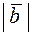, то угол между векторами (косинус угла между векторами) вычисляют по формуле
.
Если известны координаты векторов:
, 
,
то скалярное произведение вычисляется по формуле
,
а косинус угла – по формуле
.
10. 2. Свойства скалярного произведения
Свойство 1.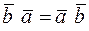 
– закон коммутативности.
Свойство 2.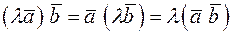 
– закон ассоциативности.
Свойство 3. 
– закон дистрибутивности.
Свойство 4.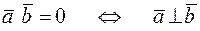 
; для того чтобы два вектора были перпендикулярны, необходимо и достаточно, чтобы их скалярное произведение равнялось нулю.
Свойство 5.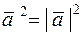 
; скалярный квадрат вектора равен квадрату его длины.
11. Векторное произведение двух векторов
11. 1. Определение векторного произведения
Определение 20. Векторным произведением векторов на вектор называется вектор 
, такой, что:
1) его длина равна площади параллелограмма, построенного на векторах и :
;
2) он перпендикулярен каждому из перемножаемых векторов:
;
3) направление вектора определяется по правилу «правой тройки», то есть кратчайший поворот от вектора (первого множителя) к вектору (второму множителю) из конца вектора виден против хода часовой стрелки.
Векторное произведение и обозначается 
.
Если известны координаты векторов:
, ,
то векторное произведение вычисляется по формулам:
|
|
|
,
.
11. 2. Свойства векторного произведения
Свойство 1. 
– закон антикоммутативности.
Свойство 2.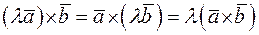 
– закон ассоциативности.
Свойство 3. 
– закон дистрибутивности.
Свойство 4. 
; для того чтобы два вектора были параллельны (коллинеарны), необходимо и достаточно, чтобы их векторное произведение равнялось нулю.
Свойство 5. 
; векторный квадрат вектора равен нулевому вектору.
Свойство 6. Геометрический смысл векторного произведения: длина векторного произведения векторов и равна площади параллелограмма, построенного на этих векторах (пункт 1) определения).
12. Смешанное произведение трёх векторов
12. 1. Определение смешанного произведения
Определение 21. Смешанным произведением трёх векторов , и называется число, скалярному произведению первого вектора на векторное произведение двух других. Смешанное произведение векторов , и обозначается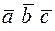 
. Таким образом,
.
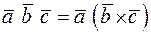В определении смешанного произведения можно векторно умножить вектор на вектор , а затем полученный вектор скалярно умножить на вектор .
Если известны координаты векторов:
, , 
,
то векторное произведение вычисляется по формулам:
,
12. 2. Свойства смешанного произведения
Свойство 1. 
;
.
Свойство 2. Геометрический смысл векторного произведения: модуль смешанного произведения векторов , и равен объёму параллелепипеда, построенного на этих векторах.
Векторы, параллельные одной плоскости, называются компланарными. Для любых двух векторов найдется плоскость, параллельная этим векторам. Поэтому, два вектора всегда компларны. Три и более количество векторов могут быть параллельными одной плоскости, и могут не быть параллельными. Следующее свойство даёт ответ на вопрос: является ли данная тройка векторов компланарной?
|
|
|
Свойство 3. 
– компланарные; для того чтобы три вектора принадлежали одной плоскости, необходимо и достаточно, чтобы их смешанное произведение равнялось нулю.
|
|
|
