 |
2. Действия над векторами. 2.1. Умножение вектора на число. 2.2. Сумма векторов. 2.3. Разность векторов. 3. Числовая ось
|
|
|
|
2. Действия над векторами
В качестве действий над векторами, рассматриваются линейные операции – умножение вектора на число, сложение и вычитание.
2. 1. Умножение вектора на число
Определение 6. Произведением вектора 
на вещественное число 
называется вектор 
, коллинеарный вектору , имеющий длину 
и сонаправленный с вектором , если 
, и противонаправленный с вектором , если 
. Произведением вектора на число обозначается 
или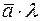 
.
На рис. 6 – рис. 9 показаны пары векторы и 
, и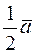 
, и 
, и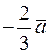 
Рис. 3. Случай 
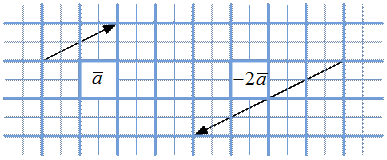
Рис. 4. Случай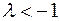 
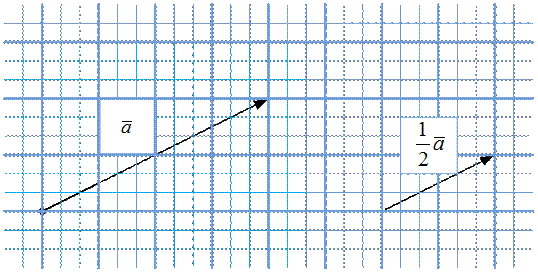
Рис. 5. Случай 
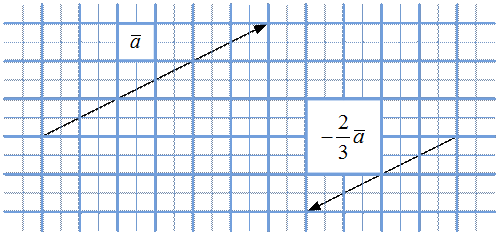
Рис. 6. Случай 
Противоположный вектор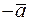 
можно рассматривать как результат умножения вектора на число 
:
.
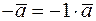Отметим некоторые свойства умножения вектора на число.
1. 
– закон коммутативности.
2. 
– закон ассоциативности.
3. 
– закон дистрибутивности.
4. 
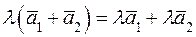– закон дистрибутивности.
Теорема 1. Для коллинеарности векторов и 
, необходимо и достаточно существование числа такого, что выполняется хотя бы одно из равенств 
или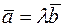 
.
2. 2. Сумма векторов
Определение 7. Суммой векторов и называется вектор , вычисляемый как диагональ параллелограмма, построенного на этих векторах, имеющая с ними общее начало (рис. 10). Сумма векторов и обозначается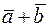 
.
Рис. 10
Отметим некоторые свойства суммы векторов.
1. 
– закон коммутативности.
2. 
– закон ассоциативности.
3. 
.
4. 
.
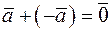2. 3. Разность векторов
Определение 8. Разностью 
векторов и называется вектор, сумма которого с вектором равна вектору . Разность можно определить как сумму вектора с вектором, противоположным к вектору : 
.
|
|
|
Разность векторов и можно вычислить по правилу параллелограмма, как диагональ этого параллелограмма, исходящей из конца вектора (рис. 11).
Сумма и разность векторов определялись по правилу параллелограмма. Можно эти две операции определить по правилу треугольника. Для определения суммы 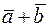, следует параллельным переносом начало вектора совмещать с концом вектора . Для определения разности , следует концы этих векторов.
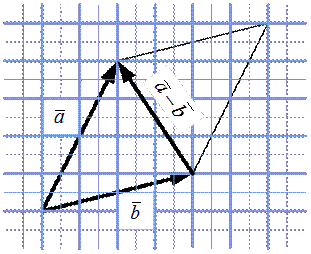
Рис. 11
3. Числовая ось
Числовой осью ( числовой прямой ) называется любая прямая, если:
1) на ней выбрана некоторая точка, называемая началом ( центром ) и обозначаемая 
;
2) любое из двух направлений, называемое положительным направлением и обозначаемое стрелкой;
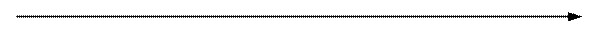
3) некоторый отрезок, называемый единичным отрезком ( масштабом ).
Каждому вещественному числу на числовой прямой соответствует единственная точка на числовой оси:
1) положительное число 
изображается точкой, расположенной на оси на расстоянии по направлению стрелки;
2) отрицательное число 
изображается точкой, расположенной на оси на расстоянии против направления стрелки;
3) нулевое число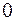 
изображается началом оси.
Имеет место и обратное соответствие: каждой точке на числовой оси соответствует единственное вещественное число.
Пусть точке 
числовой оси соответствует число . Координатой точки называется число и обозначается 
.
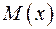4. Единичный вектор
Определение 9. Любой вектор, длина которой равна единице, называется единичным вектором.
Пусть задан вектор . Обозначим через 
единичный вектор, сонаправленный с вектором , называемый орт ом этого вектора. Из определения умножения вектора на число следует, что
или 
.
Для каждой числовой оси 
определен единичный вектор 
, с началом в точке ( – центр числовой оси) и концом в точке с координатой 
(рис. 12). Направление единичного вектора совпадает с положительным направлением числовой оси .
|
|
|
Рис. 12
|
|
|
