 |
5. Угол между векторами. 6. Проекция вектора на ось. 7. Системы координат. 7.1. Декартова система координат на плоскости
|
|
|
|
5. Угол между векторами
Определение 10. Пусть векторы 
и 
имеют общее начало. Углом между векторами и называется наименьший угол 
, на который нужно повернуть один из этих векторов до совпадения с другим (рис. 13). Под термином совпадение понимается, что векторы и окажутся сонаправленными. Угол между векторами и обозначают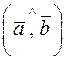 
.
Из определения вытекает, что угол между произвольными векторами содержится в промежутке: 
.
Определение 11. Пусть начало вектора находится в центре числовой оси 
. Углом между вектором и осью называется угол между вектором и единичным вектором 
оси (рис. 14).
Рис. 13 Рис. 14
6. Проекция вектора на ось
Определение 12. Проекцией точки 
на ось называется точка пересечения плоскости 
, проходящей через точку перпендикулярно оси с осью (рис. 15).
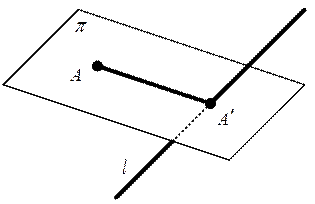
Рис. 15
Определение 13. Проекцией вектора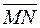 
на ось называется число, равное разности координат проекций конца и начала (рис. 16).
Рис. 16
Проекция вектора 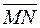на ось обозначается 
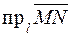. Имеем
.
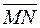Обозначим через угол между вектором и осью .
Проекция вектора может быть: 1) положительной, если угол острый. В этом случае 
(рис 16), 2) отрицательной, если угол тупой. В этом случае 
(рис. 17), 3) нулевой, если угол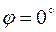 
или 
. В этом случае 
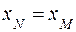(рис. 18).
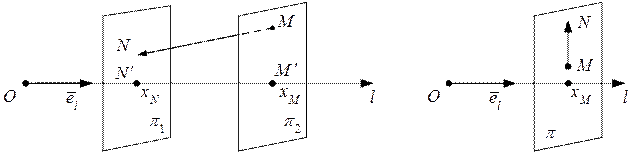
Рис. 17 Рис. 18
Определение 13. Составляющей вектора 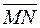по оси называется произведение проекции вектора 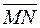на ось на единичный вектор этой оси и обозначается сост 
.
Составляющей вектора 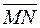по оси есть вектор, соединяющий проекцию начала и проекцию конца вектора:
|
|
|
сост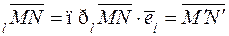 
.
Отметим некоторые свойства проекции вектора на ось.
Свойство 1. Проекция вектора на ось равна произведению длины вектора на косинус угла между вектором и осью :
.
Свойство 2. Проекция произведения вектора на число 
на ось равна произведению числа на проекцию вектора на ось :
.
Свойство 3. Проекция суммы двух векторов и на ось равна сумме проекций этих векторов на ось :
.
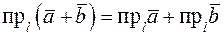Свойство 4. Проекция разности двух векторов и на ось равна разности проекций этих векторов на ось :
.
7. Системы координат
7. 1. Декартова система координат на плоскости
Определение 14. Прямоугольной системой координат на плоскости называется пара взаимно перпендикулярных числовых осей, имеющие общее начало 
. Общее начало совпадает с точкой пересечения (рис. 19).
Определение 15. Плоскость в которой, расположены оси, называется координатной плоскостью 
.
Осей, составляющих прямоугольную систему координат на плоскости обозначим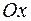 
и 
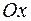. Как правило, ось на чертеже располагают горизонтально, а ось – вертикально. Произвольной точке 
плоскости соответствуют два вещественных числа (рис. 20):
1) проекция точки на ось 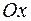и обозначают 
;
2) проекция точки на ось и обозначают 
.
Рис. 19 Рис. 20
Определение 16. Число называется абсциссой точки , число – ординатой этой точки.
Определение 17. Ось 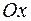называется осью абсцисс, ось – осью ординат.
Определение 18. Упорядоченная пара чисел 
называется прямоугольными ( декартовыми ) координатами точки координатной плоскости и обозначается 
.
Каждой точке координатной плоскости соответствует единственная упорядоченная пара чисел и, наоборот, каждой упорядоченной паре чисел соответствует единственная точка координатной плоскости .
|
|
|
Координатные ос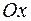и и делят координатную плоскость на четыре четверти (на четыре квадранты ). Каждая точка , не принадлежащая координатным осям, содержится в одной из четырех четвертей. Обозначение этих четвертей и знаки координат точки:
1) первая четверть – 
; 
;
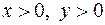2) вторая четверть –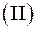 
; 
;
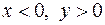3) третья четверть – 
; 
;
4) четвёртая четверть –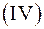 
; 
.
|
|
|
