 |
7.2. Декартова система координат в пространстве
|
|
|
|
7. 2. Декартова система координат в пространстве
Определение 19. Прямоугольной системой координат в пространстве называется тройка взаимно перпендикулярных числовых осей, имеющие общее начало 
и совпадающее с точкой пересечения.
Оси, составляющие прямоугольную систему координат в пространстве называются координатными осями и обозначаются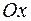 
, 
и 
:
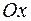– ось абсцисс;
– ось ординат;
– ось аппликат.
Положение каждой точки 
пространства определяется тремя вещественными числами. Этими числами являются:
1) проекция точки на ось 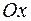; обозначают 
;
2) проекция точки на ось ; обозначают 
.
3) проекция точки на ось ; обозначают 
.
Рис. 21
Определение 18. Упорядоченная тройка чисел 
называется прямоугольными ( декартовыми ) координатами точки пространства 
и обозначается 
.
Каждой точке пространства соответствует единственная упорядоченная тройка числе и, наоборот, каждой упорядоченной тройке чисел соответствует единственная точка пространства .
Координатные ос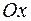и , и делят пространства на восемь октантов. Каждая точка , не принадлежащая координатным осям, содержится в одной из восьми октантов. Обозначение этих октант и знаки координат точки:
| Октант | Знаки | Октант | Знаки | ||
| 
| 
| 
| ||
| 
| 
| 
| ||
| 
| 
| 
| ||
| 
| 
| 
|
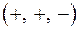
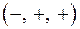
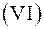
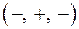
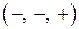
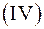
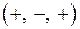
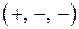
На каждой из координатных осей выберем единичный вектор с началом в точке и концом в точке с координатой 
. Обозначим:
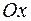– единичный вектор оси ;
– единичный вектор оси ;
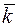– единичный вектор оси .
Эти три единичных вектора называются ортами. Они образуют декартов ортогональный базис.
|
|
|
Рассмотрим вектор 
в пространстве. Отложим его из начала координат (рис. 22). Через его конец проведем плоскости, параллельные координатным плоскостям. Получим прямоугольный параллелепипед, диагональю которого является вектор .
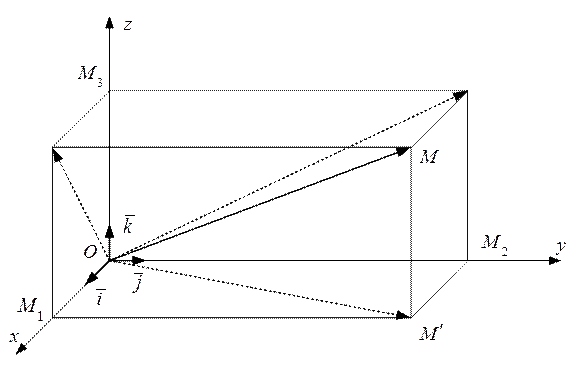
Рис. 22
Из рис. 22 ясно, что:
.
Векторы 
, 
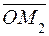и 
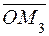являются составляющими вектора . Представив составляющие с помощью произведения проекции на единичный вектор, получим
, 
, 
.
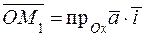Обозначив
, 
, 
,
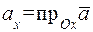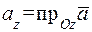будем иметь
.
Полученная формула называется разложением вектора на составляющие по координатным осям. Числа 
называются прямоугольными декартовыми координатами вектора . Координаты вектора будем записывать в виде
.
Вектор 
с началом в начале координат и концом в точке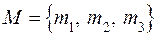 
называется радиус-вектором 
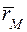точки . Координаты радиус-вектора 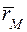совпадают с координатами точки :
или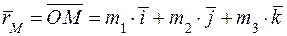 
.
Пусть 
и 
– произвольные точки пространства. Координаты вектора 
вычисляются по формуле
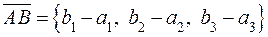
или
.
Для получения координат вектора из координаты конца нужно вычитать соответствующие координаты начала.
Если известны координаты вектора, то линейные операции над векторами можно заменить соответствующими арифметическими операциями над координатами.
Пусть , 
. Тогда
;
;
.
Если векторы заданы в виде
, 
,
то линейные операции выполняются так:
.
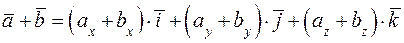
8. Длина вектора. Расстояние между двумя точками
8. 1. Длина вектора
Пусть – произвольный вектор. Длина вектора вычисляется по формуле:
.
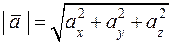8. 2. Расстояние между двумя точками
Пусть и – произвольные точки пространства. Расстояние между точками 
и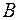 
вычисляется по формуле:
.
9. Направляющие косинусы вектора
|
|
|
Направление вектора в пространстве можно задать углами 
, 
и 
, которые составляет данный вектор с осями координат. Косинусы этих углов: 
, 
и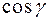 
называются направляющими косинусами вектора.
Рис. 23
Пусть – произвольный вектор. Согласно формуле проекции вектора на ось будем иметь
,
,
.
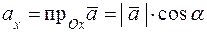Отсюда получим значения направляющих косинусов:
или
,
,
.
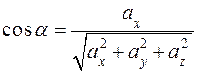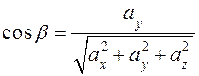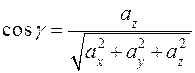Из полученных равенств вытекает следующее тождество
.
Полученное тождество означает, что среди углов , и независимыми являются только два, а третий определяется из тождества (с точностью до знака).
|
|
|
