 |
Виды ДУ, описывающих процессы в конструкциях РЭА
|
|
|
|
Процессы, протекающие в РЭА подразделяются на стационарные и нестационарные. Процесс называется стационарным, если внешние и внутренние возмущения практически не изменяются во времени. В противном случае процессы называются нестационарными. Для моделирования задач анализа конструкций отличие между стационарными и нестационарными условиями является существенным, так как методы их решения различны.
В случае стационарного режима задачу определения реакции системы называют краевой задачей, для решения которой достаточно найти величину реакции и ее распределение в конструкции. Примером краевой задачи может служить задача определения распределения температур в блоке РЭА при заданном установившемся режиме работы и постоянной температуре окружающей среды. Краевыми условиями здесь являются температура окружающей среды или плотность потока тепловой энергии обмена с окружающей средой.
В случае нестационарного режима задачу определения реакции системы называют задачей с начальными условиями (условия Коши). В таких задачах для определения реакции системы необходимо знать ее поведение в начальный и последующие моменты времени.
Задача анализа процессов в конструкциях РЭА чаще всего сводится к исследованию различных полей (например, тепловых) или механических процессов (например, вибрации), которые описываются с помощью ДУ, в состав которых входят частные производные по каждой переменной. Многие нестационарные физические процессы в пространстве описываются с помощью ДУ вида:
, (3.1)
где: 
.
Функции 
определяют параметры вещества пространства. Если среда изотропная, то 
и говорят о линейной задаче.
Значение искомой функции Y находится внутри некоторой области V, ограниченной поверхностью S – для трехмерной, и линией S – для двумерной задачи. На границе поверхности (линии) S задаются граничные условия вида:
|
|
|
где:
- a и b – заданные функции точки в граничной области;
- 
– известная в граничной области функция;
- 
– производная искомой функции по нормали к граничной области в рассматриваемой точке.
Если во всех граничных точках b = 0, то есть функция Ф во всех точках определяет значение искомой функции Y, то такие условия, обозначаемые как 
, называются граничными условиями 1-го рода. Если во всех граничных точках Y ½S = 0, а 
, то есть, определены лишь значения производной искомой функции по нормали к этой области, то такие условия считают граничными условиями 2-го рода. В том случае, когда имеют место смешанные варианты условий, то их называют граничными условиями 3-го рода.
Характер ДУ и методы его решения меняются в зависимости от величины коэффициентов a, b, c и d, которые принимают нулевые или положительные значения для различных моделей процессов.
Если a=b=0, c³0 и d³0, то получим уравнения эллиптического вида. Наиболее важным и часто встречающимся уравнением прикладной физики эллиптического вида является уравнение Лапласа, описывающее стационарное состояние поля в области без внутренних источников и стоков. Любые установившиеся процессы теплопередачи, электро- и магнитостатики описываются этим уравнением. В общем случае уравнение Лапласа имеет вид:
Ñ2 Y = 0
где: лапласиан Ñ2 представляет собой сумму вторых производных по отношению к рассматриваемым пространственным переменным. Лапласиан для трехмерного случая имеет вид:
Ñ2 Y = 
Функция Y, удовлетворяющая уравнению Лапласа, называется гармонической. Искомое решение выделяется из множества всех гармонических функций определением дополнительного условия, которое часто является краевым: 
|
|
|
Другим уравнением математической физики эллиптического вида является уравнение Пуассона, представляющее собой неоднородное уравнение относительно Лапласиана:
Ñ2 Y = d. (3.2)
Уравнение Пуассона описывает установившуюся систему, внутри которой равномерно распределены источники энергии. В электростатике к такому уравнению приводится задача с равномерно распределенным в поле зарядом. Это уравнение применяется при расчете систем теплопередачи, когда тепловая энергия генерируется внутри температурного поля (например, для определения распределения температуры по поверхности подложки микросхемы с источниками тепла – тепловыделяющими элементами схемы). Граничные условия для уравнения Пуассона определяют и записывают так же, как и для уравнения Лапласа.
При описании нестационарных процессов в конструкциях РЭА используют уравнения параболического вида. Такие уравнения получаются из обобщенной записи ДУ (3.1), если a=0; b³0, c ³0. Этот вид уравнения, решаемый для однородной области, известен как уравнение диффузии или уравнение Фурье: Ñ2 Y = 
, где: К – постоянная времени диффузии. Величина К характеризует скорость затухания процесса и перехода его в стационарный процесс. Она определяется параметрами системы.
Уравнение Фурье используется также для расчета теплового баланса температуры конструкции РЭА. В этих случаях получаем уравнение теплопроводности вида:
lÑ2 Y = 
, (3.3)
где: l и с – коэффициенты теплопроводности и теплоемкости среды соответственно. Левая часть ДУ (3.3) определяет передачу тепла между элементами конструкции с помощью теплопроводности, а правая – нагрев (или охлаждение) конструкции. Для анизотропных сред:
.
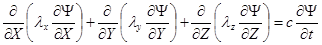Для однозначного решения этого уравнения необходимо задать граничные и начальные условия.
Если в среде присутствуют распределенные источники, то, как и в уравнении Фурье, появляется свободный член F=F(x,y,z,t), который определяет нагрев конструкции за счет внутренних источников. Таким образом, уравнения (3.2) и (3.3) примут соответственно вид:
Ñ2 Y + F(x,y,z,t) = d,
lÑ2 Y + F(x,y,z,t) = .
В случае, когда в уравнении (3.1) a>0; b³0, c ³0, d ³0, уравнения называют ДУ гиперболического вида. Сюда относятся волновые ДУ, описывающие колебательные процессы в различных средах, которые в простейшем случае имеют вид: Ñ2 Y = 
, где: К – постоянная величина, определяемая параметрами системы и характеризующая период распространения возмущений. Чем меньше величина К, тем быстрее передается возмущение от одной точки пространства к другой.
|
|
|
Для однозначного решения данного ДУ требуется задать граничные и начальные условия. Поскольку в уравнение входит вторая производная искомой функции по времени, следует задать два начальных условия. Одно представляет собой значение искомой функции в начальный момент времени 
. В качестве второго – выбирают начальное значение первой производной искомой функции по времени.
Общих методов интегрирования ДУ нет. Поэтому математики говорят не «решить задачу», а «отыскать функцию, удовлетворяющую дифференциальному уравнению».
|
|
|
